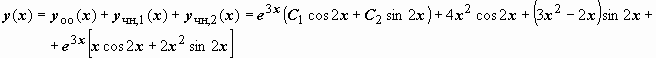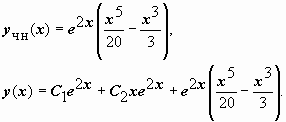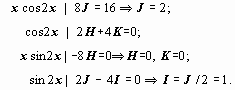- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
Метод подбора частного решения неоднородного уравнения с правой частью специального вида. Методом Лагранжа может быть решено любое неоднородное уравнение с постоянными коэффициентами. Однако если свободный член в уравнении (20) имеет вид
![]() (37)
(37)
где
Pm1(x)
и Qm2(x)
- многочлены степеней, соответственно,
m1
и m2,
можно сразу указать вид частного решения
в форме с неопределёнными коэффициентами.
Общее
правило
таково: составим из коэффициентов при
x
в экспоненте и тригонометрических
функциях число
![]() и
пусть r
- кратность числа s0
как корня характеристического уравнения,
m
= max(m1,
m2).
Тогда частное решение надо искать в
виде
и
пусть r
- кратность числа s0
как корня характеристического уравнения,
m
= max(m1,
m2).
Тогда частное решение надо искать в
виде
![]() ,
где Rm(x)
и Sm(x)
- многочлены степени m
с неопределёнными коэффициентами.
Дифференцируя функцию yчн
n
раз, подставив эти производные в уравнение
и приравнивая коэффициенты при одинаковых
степенях x
и одинаковых тригонометрических функциях
(sin x
или
cos x),
получим систему из 2(m
+ 1) уравнений относительно 2(m
+ 1) неопределённых коэффициентов
многочленов Rm(x)
и Sm(x).
Решив эту систему, определим коэффициенты
функции yчн(x).
Технику
работы с этим правилом будем осваивать,
начиная с простейших случаев, при этом
будем формулировать частные правила,
вытекающие из общего.
I.
Если f(x)
= Pm(x)
(т.е. f(x)
- многочлен степени m),
то частное решение ищется в виде yчн(x)=
Rm(x),
если число 0 не является корнем
характеристического уравнения, и в виде
yчн(x)=
xr
Rm(x),
если число 0 - корень характеристического
уравнения кратности r.
Rm(x)
- многочлен степени m
с неопределёнными коэффициентами.
Это
правило следует из общего, если записать
f(x)
= Pm(x)
в виде f(x)
= e0
x
[Pm(x)
cos 0x
+ 0 sin 0x].
В этом случае s0
= 0 + 0i,
m1
= m,
m2
= 0, max(m1,
m2)
= m,
поэтому
yчн(x)=
xr
e0
x
[Rm(x)
cos 0x
+ Sm(x)
sin 0x]
= xr
Rm(x)
.
Примеры:
1. Найти общее решение уравнения
,
где Rm(x)
и Sm(x)
- многочлены степени m
с неопределёнными коэффициентами.
Дифференцируя функцию yчн
n
раз, подставив эти производные в уравнение
и приравнивая коэффициенты при одинаковых
степенях x
и одинаковых тригонометрических функциях
(sin x
или
cos x),
получим систему из 2(m
+ 1) уравнений относительно 2(m
+ 1) неопределённых коэффициентов
многочленов Rm(x)
и Sm(x).
Решив эту систему, определим коэффициенты
функции yчн(x).
Технику
работы с этим правилом будем осваивать,
начиная с простейших случаев, при этом
будем формулировать частные правила,
вытекающие из общего.
I.
Если f(x)
= Pm(x)
(т.е. f(x)
- многочлен степени m),
то частное решение ищется в виде yчн(x)=
Rm(x),
если число 0 не является корнем
характеристического уравнения, и в виде
yчн(x)=
xr
Rm(x),
если число 0 - корень характеристического
уравнения кратности r.
Rm(x)
- многочлен степени m
с неопределёнными коэффициентами.
Это
правило следует из общего, если записать
f(x)
= Pm(x)
в виде f(x)
= e0
x
[Pm(x)
cos 0x
+ 0 sin 0x].
В этом случае s0
= 0 + 0i,
m1
= m,
m2
= 0, max(m1,
m2)
= m,
поэтому
yчн(x)=
xr
e0
x
[Rm(x)
cos 0x
+ Sm(x)
sin 0x]
= xr
Rm(x)
.
Примеры:
1. Найти общее решение уравнения
![]() .
Решение:
характеристическое уравнение k2
- 5
k
+ 6 = 0, его корни k1
=
2, k2
=
3, yoo
= C1e
2x
+
C3e
3x.
Степень многочлена m
= 3, число 0 не является корнем
характеристического уравнения (r
= 0), поэтому yчн(x)
ищем в виде многочлена третьей степени
с неопределёнными коэффициентами:
yчн(x)=
xr
Rm(x)
= Ax3
+ Bx2
+ Dx
+ E.
Тогда
.
Решение:
характеристическое уравнение k2
- 5
k
+ 6 = 0, его корни k1
=
2, k2
=
3, yoo
= C1e
2x
+
C3e
3x.
Степень многочлена m
= 3, число 0 не является корнем
характеристического уравнения (r
= 0), поэтому yчн(x)
ищем в виде многочлена третьей степени
с неопределёнными коэффициентами:
yчн(x)=
xr
Rm(x)
= Ax3
+ Bx2
+ Dx
+ E.
Тогда
![]() ;
подстановка этих выражений в уравнение
даст [6Ax
+ 2B]
- 5[3Ax2
+ 2Bx
+ D]
+ 6[Ax3
+ Bx2
+ Dx
+ E]
= x3
- 2x.
Приводим подобные члены: 6Ax3
+ [-15A
+ 6B]
x2
+ [6A
- 10B
+ 6D]
x
+ [2B
-5D
+ 6E]
= x3
- 2x.
Сравниваем коэффициенты при одинаковых
степенях x:
;
подстановка этих выражений в уравнение
даст [6Ax
+ 2B]
- 5[3Ax2
+ 2Bx
+ D]
+ 6[Ax3
+ Bx2
+ Dx
+ E]
= x3
- 2x.
Приводим подобные члены: 6Ax3
+ [-15A
+ 6B]
x2
+ [6A
- 10B
+ 6D]
x
+ [2B
-5D
+ 6E]
= x3
- 2x.
Сравниваем коэффициенты при одинаковых
степенях x:
x3 x2 x 1 |
6A = 1; - 15A + 6B =0; 6A – 10B + 6D = -2; 2B – 5D + 6E = 0; |
A = 1/6; B = 15A/6 = 5/12; D = 5B/3 – A – 1/3 = (25 – 6 – 12)/36 = 7/36; E = 5D/6 – B/3 = 35/216 – 5/36 =(35 – 30)/216 = 5/216. |
Итак,
![]()
2.
![]() .
k2
- 5
k
= 0, k1
=
0, k2
=
5, yoo
= C1
+
C3e
5x.
Степень многочлена m
= 3, число 0 является корнем характеристического
уравнения кратности r
= 1, поэтому yчн(x)
ищем в виде yчн(x)
= x(Ax3
+ Bx2
+ Dx
+ E)
= Ax4
+ Bx3
+ Dx2
+ Ex.
Тогда
.
k2
- 5
k
= 0, k1
=
0, k2
=
5, yoo
= C1
+
C3e
5x.
Степень многочлена m
= 3, число 0 является корнем характеристического
уравнения кратности r
= 1, поэтому yчн(x)
ищем в виде yчн(x)
= x(Ax3
+ Bx2
+ Dx
+ E)
= Ax4
+ Bx3
+ Dx2
+ Ex.
Тогда
![]() [12Ax2
+ 6Bx
+ 2D]
– 5[4Ax3
+ 3Bx2
+ 2Dx
+ E]
= x3
- 2xE,
[12Ax2
+ 6Bx
+ 2D]
– 5[4Ax3
+ 3Bx2
+ 2Dx
+ E]
= x3
- 2xE,
x3 x2 x 1 |
- 20A = 1; 12A - 15B =0; 6B - 10D = -2; 2D - 5E = 0; |
A = - 1/20; B = 4A/5 = - 1/25; D = 3B/5 + 2/10 = - 3/125 + 2/10 = 44/250 = 22/125; E = 2D/5 = 44/625. |
![]()
3.
![]() .
k4 - 5 k2
= 0, k2 (k2 - 5) =
0, k1,2 = 0,
.
k4 - 5 k2
= 0, k2 (k2 - 5) =
0, k1,2 = 0,
![]() ,
,
![]() .
Степень многочлена m = 3, число 0
является корнем характеристического
уравнения кратности r = 2, поэтому
yчн(x) ищем в виде
yчн(x) = x2(Ax3
+ Bx2 + Dx + E)
= Ax5 + Bx4 + Dx3
+ Ex2. Тогда
.
Степень многочлена m = 3, число 0
является корнем характеристического
уравнения кратности r = 2, поэтому
yчн(x) ищем в виде
yчн(x) = x2(Ax3
+ Bx2 + Dx + E)
= Ax5 + Bx4 + Dx3
+ Ex2. Тогда
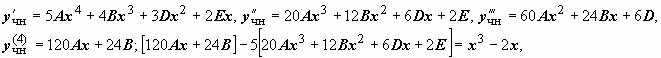
x3 x2 x 1 |
- 100A = 1; 60B =0; 120A - 30D = -2; 24B - 10E = 0; |
A = - 1/100; B = 0; D = 4A/5 + 2/30 = - 4/100 + 2/30 = 8/300 = 2/75; E = 24B/10 = 0. |
![]() II.
Если
II.
Если
![]() ,
то частное решение ищется в виде
,
то частное решение ищется в виде
![]() ,
если число
не
является корнем характеристического
уравнения, и в виде
,
если число
не
является корнем характеристического
уравнения, и в виде
![]() ,
если число
-
корень характеристического уравнения
кратности r.
Rm(x)
- многочлен степени m
с неопределёнными коэффициентами.
Это
правило следует из общего, если записать
,
если число
-
корень характеристического уравнения
кратности r.
Rm(x)
- многочлен степени m
с неопределёнными коэффициентами.
Это
правило следует из общего, если записать
![]() в
виде
в
виде
![]() .
В этом случае
.
В этом случае
![]() ,
поэтому
,
поэтому
![]() .
Примеры:
4. Найти общее решение уравнения
.
Примеры:
4. Найти общее решение уравнения
![]() .
Решение:
характеристическое уравнение k2
- 4
k
+ 4 = 0, (k
- 2)2
= 0, его корни k1,2
=
2, уоо
= С1е2x
+ С2
хе2x
. Степень многочлена m
= 3, число
.
Решение:
характеристическое уравнение k2
- 4
k
+ 4 = 0, (k
- 2)2
= 0, его корни k1,2
=
2, уоо
= С1е2x
+ С2
хе2x
. Степень многочлена m
= 3, число
![]() является
корнем характеристического уравнения
кратности r
= 2, поэтому yчн(x)
ищем в виде yчн(x)
= x2
e2x[Ax3
+ Bx2
+ Dx
+ E]
= e2x
(Ax5
+ Bx4
+ Dx3
+ Ex2).
Тогда
является
корнем характеристического уравнения
кратности r
= 2, поэтому yчн(x)
ищем в виде yчн(x)
= x2
e2x[Ax3
+ Bx2
+ Dx
+ E]
= e2x
(Ax5
+ Bx4
+ Dx3
+ Ex2).
Тогда
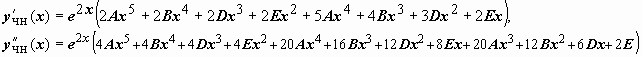 Подстановка
этих выражений в уравнение даст
Подстановка
этих выражений в уравнение даст
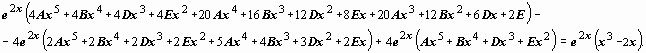 После
приведения подобных членов и сокращения
на e2x
сравниваем
коэффициенты при одинаковых степенях
x:
После
приведения подобных членов и сокращения
на e2x
сравниваем
коэффициенты при одинаковых степенях
x:
x3 x2 x 1 |
20A = 1; 12B =0; 6D = -2; 2E = 0; |
A = 1/20; B = 0; D = - 1/3; E = 0. |
|
5.
![]() .
k2
- 5
k
+ 6 = 0, k1
=
2, k2
=
3, yoo
= C1e
2x
+
C3e
3x.
m
= 3, число
является
корнем характеристического уравнения
кратности r
= 1, поэтому yчн(x)
ищем в виде yчн(x)
= x1
e2x
(Ax3
+ Bx2
+ Dx
+ E)
= e2x
(Ax4
+ Bx3
+ Dx2
+ Ex).
Дальнейшие выкладки проводятся также,
как и в предыдущих примерах.
6.
.
k2
- 5
k
+ 6 = 0, k1
=
2, k2
=
3, yoo
= C1e
2x
+
C3e
3x.
m
= 3, число
является
корнем характеристического уравнения
кратности r
= 1, поэтому yчн(x)
ищем в виде yчн(x)
= x1
e2x
(Ax3
+ Bx2
+ Dx
+ E)
= e2x
(Ax4
+ Bx3
+ Dx2
+ Ex).
Дальнейшие выкладки проводятся также,
как и в предыдущих примерах.
6.
![]() .
.
![]() ,
,
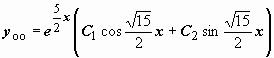 .
m
= 3, число
не
является корнем характеристического
уравнения, поэтому yчн(x)
= e2x
(Ax3
+ Bx2
+ Dx
+ E).
Дальнейшие выкладки опускаем.
.
m
= 3, число
не
является корнем характеристического
уравнения, поэтому yчн(x)
= e2x
(Ax3
+ Bx2
+ Dx
+ E).
Дальнейшие выкладки опускаем.
Пример на применение общего правила:
7.
![]() .
.
![]() ,
yoo
= e3x(C1
cos 2x
+ C2
sin 2x).
Правая часть состоит из двух слагаемых,
притом структура этих слагаемых различна:
второе содержит функцию e3x,
первое - нет (более точно, первое содержит
функцию e0x
= 1), поэтому мы должны искать два частных
решения (т.е. воспользоваться теоремой
14.5.9.2 о наложении решений).
Ищем первое частное решение, удовлетворяющее
уравнению
,
yoo
= e3x(C1
cos 2x
+ C2
sin 2x).
Правая часть состоит из двух слагаемых,
притом структура этих слагаемых различна:
второе содержит функцию e3x,
первое - нет (более точно, первое содержит
функцию e0x
= 1), поэтому мы должны искать два частных
решения (т.е. воспользоваться теоремой
14.5.9.2 о наложении решений).
Ищем первое частное решение, удовлетворяющее
уравнению
![]() .
Запишем правую часть как f(x)
= (75x2
– 86x
+ 18) sin 2x
= e0x[0
cos 2x
+ (75x2
– 86x
+ 18) sin 2x
]. Здесь
.
Запишем правую часть как f(x)
= (75x2
– 86x
+ 18) sin 2x
= e0x[0
cos 2x
+ (75x2
– 86x
+ 18) sin 2x
]. Здесь
![]() число
s0
не является корнем характеристического
уравнения (r
=
0), m
= max(m1,
m2)
= 2 (это означает, что в качестве
коэффициентов и при sin 2x,
и при cos 2x
мы должны взять многочлены второй
степени, несмотря на то, что cos 2x
в функции f(x)
отсутствует), поэтому yчн,1(x)
= е0x[(Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x]
= (Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x.
Находим производные этой функции и
подставляем в уравнение:
число
s0
не является корнем характеристического
уравнения (r
=
0), m
= max(m1,
m2)
= 2 (это означает, что в качестве
коэффициентов и при sin 2x,
и при cos 2x
мы должны взять многочлены второй
степени, несмотря на то, что cos 2x
в функции f(x)
отсутствует), поэтому yчн,1(x)
= е0x[(Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x]
= (Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x.
Находим производные этой функции и
подставляем в уравнение:
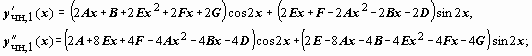 (2A+8Ex+4F-4Ax2-4Bx-4D)cos2x+(2E-8Ax-4B-4Ex2-4Fx-4G)sin2x-
-6[(2Ax+B+2Ex2+2Fx+2G)cos2x+[(2Ex+F-2Ax2-2Bx-2D)sin2x]+13[(Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x]=
= (75x2
-86 x
+ 18) sin 2x
Сравниваем
коэффициенты при одинаковых
тригонометрических функциях и одинаковых
степенях x:
(2A+8Ex+4F-4Ax2-4Bx-4D)cos2x+(2E-8Ax-4B-4Ex2-4Fx-4G)sin2x-
-6[(2Ax+B+2Ex2+2Fx+2G)cos2x+[(2Ex+F-2Ax2-2Bx-2D)sin2x]+13[(Ax2
+ Bx
+ D)
cos 2x
+ (Ex2
+ Fx
+ G)
sin 2x]=
= (75x2
-86 x
+ 18) sin 2x
Сравниваем
коэффициенты при одинаковых
тригонометрических функциях и одинаковых
степенях x:
x2cos2x x cos2x cos2x x2sin2x x sin2x sin2x |
-4A – 12E + 13A = 0; 9A =12E; 3A =4E; 8E – 4B – 12A – 12F + 13B = 0; 2A + 4F – 4D – 6B – 12G + 13D = 0; -4E + 12A + 13E =75;9E +12A =75; 3E +4A=25; -8A - 4F – 12E + 12B + 13F = 86; 2E - 4B - 4G - 6F + 12D + 13G =18; |
Из
первого и четвёртого уравнений находим
A
= 4/3E,
3E
+ 16/3E
= 25, 25/3E
=25, E
= 3, A
= 4. Перепишем второе и четвёртое
уравнения с найденными значениями
|
Решая
систему
![]() находим
9B
+ 16B
= 24 – 24 = 0, B
= 0, F
= -2. Третьё и шестое уравнения теперь
примут вид
находим
9B
+ 16B
= 24 – 24 = 0, B
= 0, F
= -2. Третьё и шестое уравнения теперь
примут вид
![]() ,
откуда D
= G
= 0.
Окончательно учн,1(x)
= 4x2
cos 2x
+ (3x2
-2x
) sin 2x.
Ищем
второе частное решение, удовлетворяющее
уравнению
,
откуда D
= G
= 0.
Окончательно учн,1(x)
= 4x2
cos 2x
+ (3x2
-2x
) sin 2x.
Ищем
второе частное решение, удовлетворяющее
уравнению
![]() .
Запишем правую часть как f(x)
= e3x[16x
cos 2x
+ 0 sin 2x
]. Здесь
.
Запишем правую часть как f(x)
= e3x[16x
cos 2x
+ 0 sin 2x
]. Здесь
![]() число
s0
является корнем характеристического
уравнения кратности r
= 1, m
= max(m1,
m2)
= 1 (т.е. в качестве коэффициентов и при
sin 2x,
и при cos 2x
мы должны взять многочлены первой
степени), поэтому yчн,2(x)
= е3x[(Hx
+ I)
cos 2x
+ (Jx
+ K)
sin 2x]
x
r
= [(Hx2
+ Ix)
cos 2x
+ (Jx2
+ Kx)
sin 2x].
Находим производные этой функции
число
s0
является корнем характеристического
уравнения кратности r
= 1, m
= max(m1,
m2)
= 1 (т.е. в качестве коэффициентов и при
sin 2x,
и при cos 2x
мы должны взять многочлены первой
степени), поэтому yчн,2(x)
= е3x[(Hx
+ I)
cos 2x
+ (Jx
+ K)
sin 2x]
x
r
= [(Hx2
+ Ix)
cos 2x
+ (Jx2
+ Kx)
sin 2x].
Находим производные этой функции
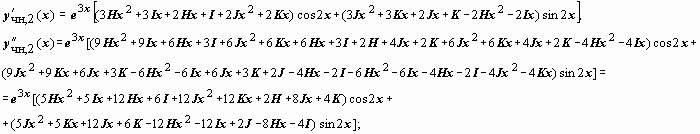 подставляем
их в уравнение:
подставляем
их в уравнение:
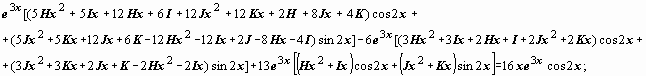 Сравниваем
коэффициенты:
Сравниваем
коэффициенты:
|
Итак,
|
Окончательный
ответ: