2. Уравнения, не содержащие явно независимой переменной.
Рассмотрим уравнения вида
.
(3)
С
помощью замены
(где
p=p(y)
- новая искомая функция независимая
переменная) порядок уравнения (3)
понижается на единицу, так как
,
.
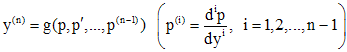Данная подстановка дает уравнение (n-1) - го порядка относительно новой неизвестной функции p:
.
При осуществлении такой замены возможна
потеря решения y=const.
Непосредственной подстановкой необходимо
проверить наличие у уравнения (3) решений
такого вида.
Пример
2.
Решить уравнение
.
Решение. Уравнение не содержит явно переменную x, делая замену , уравнение запишется в виде
.
Отсюда
находим
.
Из первого из двух последних уравнений
получаем y=C,
а из второго имеем
,
или
,
откуда
.
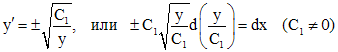Интегрируя, находим
.
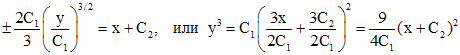Окончательно имеем
,
где
- новая произвольная постоянная.
3. Уравнения, однородные относительно .
Рассмотрим уравнения вида
, (4)
где F является однородной с показателем m относительно , т.е.
.
С
помощью замены
,
где u
- новая неизвестная функция, порядок
уравнения (4) понижается на единицу.
Имеем
,. 
.
Данная подстановка дает дифференциальное уравнение (n-1) - го порядка относительно новой неизвестной функции u:
.
Пример
3.
Решить уравнение
.
Решение.
Поскольку
функция
вследствие
тождества
однородная
относительно переменных
,
то данное дифференциальное уравнение
однородное с показателем однородности
2. Следовательно, применив подстановку
,
получим уравнение
.
Это
уравнение Риккати. Непосредственной
проверкой можно убедится, что
есть
частное решение. Поэтому посредством
подстановки
приходим
к линейному уравнению
,
решая которое, получаем окончательный ответ
.
4. Обобщенно - однородные уравнения.
Рассмотрим уравнения вида
. (5)
Уравнение (5) называется обобщенно - однородным, если существуют числа k и m такие, что
.
С
помощью замены (при x<0
полагаем
)
,
где t - новая независимая переменная, u - новая искомая функция, уравнение (5) приводит к уравнению, не содержащему независимой переменной t и, следовательно, допускающему понижение порядка на единицу (см. п. 2).
Производные при данной замене преобразуются по формулам
.
Подстановка последних равенств в (5) дает уравнение вида
,
которое явно не содержит независимую переменную t.
Пример
4.
Решить уравнение 
.
Решение.
Проверим,
что уравнение является однородным. С
этой целью вместо переменных
подставим
в выражение для функции
соответственно
и,
если это возможно, подберем значение k
таким образом, чтобы выполнялось
тождество
.
Очевидно,
что такое тождество выполняется лишь
при условии 4k=2,
т.е при k=1/2
(при этом m=2).
Следовательно, данное уравнение обобщенно
однородное. Применив подстановку
,
получим уравнение
.
Последнее
уравнение явно не содержит переменную
t,
поэтому посредством замены
понижаем
порядок на единицу:
.
Проинтегрировав последнее уравнение, находим
.Далее,
интегрируем уравнение
:
и получаем окончательно решения уравнение в виде
.
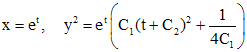5. Уравнение в точных производных.
Рассмотрим уравнения вида
, (1)
левые
части которых являются точными
производными от некоторой функции
,
т.е.
.Такие
уравнения называются уравнениями
в точных производных.
Из последнего равенства следует, что
соотношение
является первым интегралом уравнения (1) - уравнением (n-1) - го порядка относительно искомой функции. Таким образом, уравнение в точных производных допускают понижение порядка на единицу.
Пример
5.
Решить уравнение 
.
Решение.
Имеем
,откуда
следует, что
,или
.
Это линейное уравнение первого порядка, и его общее решение имеет вид
.