
- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
4. Линейные уравнения. Определение, методы решений, примеры
Линейные уравнения. ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная входят в уравнение в первой степени
![]() (14)
(14)
Здесь
p(x),
q(x)
- непрерывные функции.
Для решения
уравнения (14) представим y(x)
в виде произведения двух новых неизвестных
функций u(x)
и v(x):
y(x)
= u(x)
v(x).
Тогда
![]() ,
и уравнение приводится к виду
,
и уравнение приводится к виду
![]() ,
или
,
или
![]() .
Это уравнение решаем в два этапа: сначала
находим функцию v(x)
как частное решение уравнения с
разделяющимися переменными
.
Это уравнение решаем в два этапа: сначала
находим функцию v(x)
как частное решение уравнения с
разделяющимися переменными
![]() ;
затем находим u(x)
из уравнения
;
затем находим u(x)
из уравнения
![]() .
Итак,
.
Итак,
![]() (мы
не вводим в это решение произвольную
постоянную C,
нам достаточно найти одну функцию v(x),
обнуляющую слагаемое со скобками в
уравнении
).
Теперь уравнение для u(x)
запишется как
(мы
не вводим в это решение произвольную
постоянную C,
нам достаточно найти одну функцию v(x),
обнуляющую слагаемое со скобками в
уравнении
).
Теперь уравнение для u(x)
запишется как
![]()
![]() .
Общее решение уравнения
.
Общее решение уравнения
![]() .
Запоминать эту формулу не надо, лучше
усвоить порядок действий и воспроизводить
его при решении каждой задачи.
Пример:
.
Запоминать эту формулу не надо, лучше
усвоить порядок действий и воспроизводить
его при решении каждой задачи.
Пример:
![]() .
Решение:
.
Решение:
![]()
![]() .
Теперь для u(x)
получим:
.
Теперь для u(x)
получим:
![]() ,
и общее решение уравнения
,
и общее решение уравнения
![]() .
Для нахождения частного решения,
соответствующего начальным условиям
задачи Коши, подставим в общее решение
.
Для нахождения частного решения,
соответствующего начальным условиям
задачи Коши, подставим в общее решение
![]() .
Решение задачи:
.
Решение задачи:
![]() .
Этот
метод решения линейных уравнений часто
реализуется по-другому - в форме вариации
произвольной постоянной. Уравнение
(14) называется однородным, если q(x)
= 0. Пусть дано неоднородное уравнение
(14)
.
Этот
метод решения линейных уравнений часто
реализуется по-другому - в форме вариации
произвольной постоянной. Уравнение
(14) называется однородным, если q(x)
= 0. Пусть дано неоднородное уравнение
(14)
![]() .
Оно, как и в предыдущем случае, решается
в два этапа. Обнулим правую часть,
получившееся уравнение будем называть
однородным уравнением, соответствующим
уравнению (14):
.
Оно, как и в предыдущем случае, решается
в два этапа. Обнулим правую часть,
получившееся уравнение будем называть
однородным уравнением, соответствующим
уравнению (14):
![]() .
Решаем это уравнение:
.
Решаем это уравнение:
![]() (при
делении на y
теряется решение y
(x)
= 0, но оно входит в общее решение при C
= 0). Теперь ищем общее решение уравнения
(14) в виде
(при
делении на y
теряется решение y
(x)
= 0, но оно входит в общее решение при C
= 0). Теперь ищем общее решение уравнения
(14) в виде
![]() ,
где
,
где
![]() -
новая неизвестная функция; находим
производную
-
новая неизвестная функция; находим
производную
![]() и
подставляем в (14) y
и
и
подставляем в (14) y
и
![]() :
:
![]() ,
или
,
или
![]() ,
где
,
где
![]() .
Теперь
.
Теперь
![]() .
Понятно, что обе реализации решения
имеют один смысл (решение однородного
уравнения играет роль функции v(x),
варьируемая постоянная C(x)
- роль функции u(x)).
Отметим ещё одно важное обстоятельство.
Переменные x
и y,
входящие в уравнение, равноправны,
поэтому при определении типа уравнения
надо иметь в виду, что может оказаться
предпочтительней искать решение в виде
x
= x(y),
а не в виде y
= y(x).
Пример:
(x
+ y2)dy
= ydx.
Если мы представим это уравнение в виде
.
Понятно, что обе реализации решения
имеют один смысл (решение однородного
уравнения играет роль функции v(x),
варьируемая постоянная C(x)
- роль функции u(x)).
Отметим ещё одно важное обстоятельство.
Переменные x
и y,
входящие в уравнение, равноправны,
поэтому при определении типа уравнения
надо иметь в виду, что может оказаться
предпочтительней искать решение в виде
x
= x(y),
а не в виде y
= y(x).
Пример:
(x
+ y2)dy
= ydx.
Если мы представим это уравнение в виде
![]() ,
то решить его не сможем, так как оно не
принадлежит ни одному из рассмотренных
типов. Если же представить его в виде
,
то решить его не сможем, так как оно не
принадлежит ни одному из рассмотренных
типов. Если же представить его в виде
![]() ,
то относительно функции x
= x(y)
оно линейно. Решаем его методом вариации
произвольной постоянной. Соответствующее
однородное уравнение:
,
то относительно функции x
= x(y)
оно линейно. Решаем его методом вариации
произвольной постоянной. Соответствующее
однородное уравнение:
![]() .
Его решение:
.
Его решение:
![]() .
Ищем решение данного уравнения в форме
x
= C(y)
y. Тогда
.
Ищем решение данного уравнения в форме
x
= C(y)
y. Тогда
![]() (постоянная
C0
переобозначена как
(постоянная
C0
переобозначена как
![]() ).
Утерянное решение - y
= 0.
).
Утерянное решение - y
= 0.
5. Уравнение Бернулли. Определение, методы решений, примеры
Уравнение Бернулли. Так называется уравнение
![]() (15)
(15)
где
![]() (при
m
= 0 уравнение линейно, при m
= 1 - с разделяющимися переменными). Это
уравнение решается одним из следующих
способов:
1. Уравнение Бернулли
сводится к линейному подстановкой z
= y1-m
(при m>1
может быть потеряно решение y
= 0). Действительно,
(при
m
= 0 уравнение линейно, при m
= 1 - с разделяющимися переменными). Это
уравнение решается одним из следующих
способов:
1. Уравнение Бернулли
сводится к линейному подстановкой z
= y1-m
(при m>1
может быть потеряно решение y
= 0). Действительно,
![]() ,
,
![]() ;
после деления уравнения (15) на ym
получим
;
после деления уравнения (15) на ym
получим
![]() ,
или
,
или
![]() -
линейное уравнение.
Пример:
-
линейное уравнение.
Пример:
![]() (уравнение
Бернулли, m
= 2). Подстановка
(уравнение
Бернулли, m
= 2). Подстановка
![]() .
Решаем полученное линейное уравнение:
.
Решаем полученное линейное уравнение:
![]()
![]()
![]() .
2. Можно сразу решать уравнение
Бернулли методом, которым решаются
линейные уравнения, т.е. заменой y(x)
= u(x)
v(x):
.
2. Можно сразу решать уравнение
Бернулли методом, которым решаются
линейные уравнения, т.е. заменой y(x)
= u(x)
v(x):
![]()
![]() из
этого выражения находим u(x),
и y(x)
= u(x)
v(x).
Пример: решить задачу Коши
из
этого выражения находим u(x),
и y(x)
= u(x)
v(x).
Пример: решить задачу Коши
![]() Как
и в предыдущем примере, это уравнение
не попадает ни под один из рассмотренных
типов: оно не является ни уравнением с
разделяющимися переменными (наличие
суммы x2
+ y),
ни уравнением с однородной правой частью
(слагаемые разных порядков - первого и
второго в этой сумме), ни линейным, ни
Бернулли (другая структура). Попробуем
опять представим это уравнение как
уравнение относительно x
= x(y):
Как
и в предыдущем примере, это уравнение
не попадает ни под один из рассмотренных
типов: оно не является ни уравнением с
разделяющимися переменными (наличие
суммы x2
+ y),
ни уравнением с однородной правой частью
(слагаемые разных порядков - первого и
второго в этой сумме), ни линейным, ни
Бернулли (другая структура). Попробуем
опять представим это уравнение как
уравнение относительно x
= x(y):
![]() Это
уже уравнение Бернулли с m
= -1. Начальное условие примет вид x(1)
= 2. Решаем уравнение:
Это
уже уравнение Бернулли с m
= -1. Начальное условие примет вид x(1)
= 2. Решаем уравнение:
![]()
![]() .
Тогда
.
Тогда
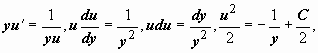
![]() .
Это общее решение уравнения (утерянное
решение y
= 0 не удовлетворяет начальному условию).
Ищем частное решение, удовлетворяющее
начальному условию:
.
Это общее решение уравнения (утерянное
решение y
= 0 не удовлетворяет начальному условию).
Ищем частное решение, удовлетворяющее
начальному условию:
![]() ;
решение задачи Коши:
;
решение задачи Коши:
![]() .
.
