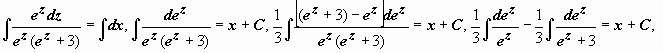- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
2. Решение уравнений с разделяющимися переменными, примеры
Уравнения с разделёнными переменными. Так называются уравнения вида удовлетворяющее начальному условию
f(x) dx + g(y) dy = 0. (10)
Пусть
y(x)
- решение этого уравнения, т.е. f(x)dx
+ g(y(x))dy(x)
= 0. Интегрируя это тождество, получим
![]() -
общий интеграл (общее решение) этого
уравнения.
Пример:
решить задачу Коши
-
общий интеграл (общее решение) этого
уравнения.
Пример:
решить задачу Коши
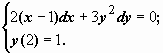 Исходное
уравнение - с разделёнными переменными,
интегрируя его, получим
Исходное
уравнение - с разделёнными переменными,
интегрируя его, получим
![]() .
Соотношение (x-1)2
+ y3
= C
- общее решение (общий интеграл) уравнения;
для того, чтобы найти частное решение,
удовлетворяющее начальному условию,
надо подставить в общее решения данные
значения x0
и y0,
и найти значение постоянной C
на этом решении: (2-1)2
+ 13
= 2
.
Соотношение (x-1)2
+ y3
= C
- общее решение (общий интеграл) уравнения;
для того, чтобы найти частное решение,
удовлетворяющее начальному условию,
надо подставить в общее решения данные
значения x0
и y0,
и найти значение постоянной C
на этом решении: (2-1)2
+ 13
= 2
![]() C
= 2. Таким образом, решение поставленной
задачи: (x-1)2
+ y3
= 2.
Уравнения
с разделяющимися переменными.
Так называются уравнения вида
C
= 2. Таким образом, решение поставленной
задачи: (x-1)2
+ y3
= 2.
Уравнения
с разделяющимися переменными.
Так называются уравнения вида
![]() или (11)
или (11)
f1(x) g1(y) dx + f2(x) g2(y) dy = 0 (12)
Эти уравнения легко сводятся к уравнению с разделёнными переменными:
Записываем
уравнение (11) в форме
|
|
Уравнение
(12) делим на f2(x)
g1(y):
|
Эти уравнения - с разделёнными переменными. Интегрируя, получим общие интегралы: |
||
|
|
|
В обоих случаях возможна потеря решений: деление на функцию может привести к уравнению, которое неэквивалентно данному. |
||
Если функция g(y) имеет действительные корни y1, y2, y3, …, то функции y = y1, y = y2, y = y3, …, очевидно, являются решениями исходного уравнения. |
|
Если функция f2(x) имеет действительные корни x1, x2, x3, …, функция g1(y) имеет действительные корни y1, y2, y3, …, то функции x = x1, x = x2, x = x3, …, y = y1, y = y2, y = y3, … являются решениями исходного уравнения. |
В обоих случаях эти решения могут содержаться в общем решении, но могут и не содержаться в нём; последнее может случиться, если на этих решениях нарушаются условия теоремы существования и единственности решения задачи Коши. |
||
Примеры:
1.
![]() .
При
такой форме записи общего интеграла
решение y
= 1 потеряно. Можно преобразовать общее
решение к виду, который содержит это
решение. Переобозначим постоянную C
как ln|C1|:
.
При
такой форме записи общего интеграла
решение y
= 1 потеряно. Можно преобразовать общее
решение к виду, который содержит это
решение. Переобозначим постоянную C
как ln|C1|:
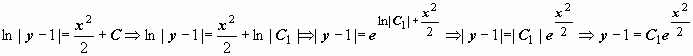 .
Вернёмся к обозначению постоянной
интегрирования C;
общее решение
.
Вернёмся к обозначению постоянной
интегрирования C;
общее решение
![]() содержит
частное решение y
= 1 при C
= 0.
2. Найти решение задачи Коши
содержит
частное решение y
= 1 при C
= 0.
2. Найти решение задачи Коши
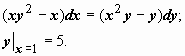 Решаем
уравнение:
Решаем
уравнение:
![]() .
Здесь могут быть потеряны решения
.
Здесь могут быть потеряны решения
![]() постоянная
интегрирования записана как
постоянная
интегрирования записана как
![]() .
Далее,
.
Далее,
![]() .
Общий интеграл уравнения
.
Общий интеграл уравнения
y2
= C(x2
– 1) + 1. Частные решения
![]() содержатся
в общем интеграле при C
= 0, решения
содержатся
в общем интеграле при C
= 0, решения
![]() утеряны
(понятно, почему это произошло: если
записать уравнение в форме, решённой
относительно производной,
утеряны
(понятно, почему это произошло: если
записать уравнение в форме, решённой
относительно производной,
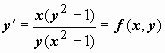 ,
то, очевидно, на решениях
нарушаются
условия, налагаемые теоремой Коши на
правую часть уравнения). Всё множество
решений: y2
= C(x2
– 1) + 1, x
= 1, x
= -1. Мы должны найти ещё частное решение,
удовлетворяющее начальному условию
y(1)
= 5. Подстановка значений x
= 1, y
= 5 в общий интеграл даёт 25=1, т.е. общий
интеграл этого частного решения не
содержит. Решение x
= 1 удовлетворяет начальному условию,
это и есть решение задачи Коши.
,
то, очевидно, на решениях
нарушаются
условия, налагаемые теоремой Коши на
правую часть уравнения). Всё множество
решений: y2
= C(x2
– 1) + 1, x
= 1, x
= -1. Мы должны найти ещё частное решение,
удовлетворяющее начальному условию
y(1)
= 5. Подстановка значений x
= 1, y
= 5 в общий интеграл даёт 25=1, т.е. общий
интеграл этого частного решения не
содержит. Решение x
= 1 удовлетворяет начальному условию,
это и есть решение задачи Коши.
К
уравнениям с разделяющимися переменными
сводятся уравнения вида
![]() (
(![]() - постоянные). Если перейти к новой
неизвестной функции z
= ax
+ by
+ c,
то
- постоянные). Если перейти к новой
неизвестной функции z
= ax
+ by
+ c,
то
![]() ,
и уравнение представляется как
,
и уравнение представляется как
![]() .
Это - уравнение с разделяющимися
переменными.
Пример:
.
Это - уравнение с разделяющимися
переменными.
Пример:
![]() .
.
![]()