
- •Функции нескольких переменных
- •1. Основные понятия
- •2. Предел и непрерывность фнп
- •3. Частные производные фнп
- •4. Полный дифференциал фнп
- •5. Дифференциалы высших порядков
- •6. Дифференцирование сложных функций
- •7. Дифференцирование неявных функций
- •8. Касательная плоскость и нормаль к поверхности.
- •9. Геометрический смысл полного дифференциала первого порядка
- •10. Производная по направлению
- •11. Градиент скалярного поля
- •12. Формула Тейлора для фнп
- •13. Экстремум функции нескольких переменных
- •14. Условный экстремум
- •1. Числовые ряды. Сходимость и расходимость числовых рядов
- •2. Необходимый признак сходимости ряда
- •3. Признаки сравнения числовых рядов
- •4. Признаки Даламбера и Коши
- •5. Интегральный признак сходимости
- •6. Знакочередующиеся ряды. Признак Лейбница
- •7. Абсолютная сходимость рядов
- •8. Действия над рядами
- •9. Степенные ряды. Определение.
- •10. Интервал сходимости степенного ряда. Теорема Абеля
- •11. Свойства степенных рядов
- •12. Разложение функций в степенные ряды. Ряды Тейлора и Маклорена
- •Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
- •Дифференциальные уравнения
- •1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
- •2. Решение уравнений с разделяющимися переменными, примеры
- •Однородные функции. Решение однородных ду первого порядка, примеры
- •4. Линейные уравнения. Определение, методы решений, примеры
- •5. Уравнение Бернулли. Определение, методы решений, примеры
- •6. Уравнения в полных дифференциалах, метод решения, примеры
- •7. Определение ду второго порядка. Решение ду, задача Коши, общее и частное решения
- •8. Решение уравнений, допускающих понижение порядка, примеры
- •1. Уравнения, не содержащие искомой функции и нескольких последовательных производных.
- •2. Уравнения, не содержащие явно независимой переменной.
- •3. Уравнения, однородные относительно .
- •4. Обобщенно - однородные уравнения.
- •5. Уравнение в точных производных.
- •9. Линейные однородные ду второго порядка. Свойства решений. Линейная зависимость решений. Общее решение
- •10. Линейные неоднородные ду второго порядка. Теорема о структуре общего решения.
- •5.1. Структура общего решения лнду второго порядка
- •11. Метод вариации постоянных для нахождения частного решения неоднородных ду второго порядка
- •5.2. Метод вариации произвольных постоянных
- •12. Линейные ду второго порядка с постоянными коэффициентами. Характеристическое уравнение. Теорема об общем решении однородного уравнения
- •13. Линейные ду 2-го порядка с постоянными коэффициентами. Правила подбора частного решения неоднородного уравнения по правой части уравнения
Разложение некоторых элементарных функций в ряды Тейлора и Маклорена
1. Разложение функции f(x)=ex в ряд Маклорена.
f(x)=f′(x)=f″(x)=…=f(n)(x)=…=ex.
f(0)=f′(0)=f″(0)=…=f(n)(0)=…=1.
Составим
для функции f(x)=ex
формально ряд Маклорена: 1+
![]() .
.
Найдём области сходимости этого ряда.
![]() при
любых x,
следовательно, областью сходимости
ряда является промежуток (-∞;+∞).
Заметим, что так как ряд сходится
абсолютно, то
при
любых x,
следовательно, областью сходимости
ряда является промежуток (-∞;+∞).
Заметим, что так как ряд сходится
абсолютно, то
![]() при любых х
и тем более
при любых х
и тем более
![]() при любых х.
Так как f(n+1)(x)=ex
и f(n+1)(с)=eс,
то
при любых х.
Так как f(n+1)(x)=ex
и f(n+1)(с)=eс,
то
![]()
![]() =ec
=ec
![]() =0.
Таким образом, имеет место разложение
при x
(-∞;+∞)
=0.
Таким образом, имеет место разложение
при x
(-∞;+∞)
ex=1+ . (32)
2. Разложение функции f(x)=sinx в ряд Маклорена.
Вычислим
производные данной функции.
f′(x)=cosx=sin(x+
![]() ),
f″(x)=-sinx=sin(x+
),
f″(x)=-sinx=sin(x+
![]() ),
),
f″′(x)=-cosx=sin(x+
![]() ),
f(4)(x)=sinx=sin(x+
),
f(4)(x)=sinx=sin(x+
![]() ),
…,
f(n)(x)=sin(x+
),
…,
f(n)(x)=sin(x+
![]() ),
…
. Вычислим
значения f(x)
и производных в точке 0:
f(0)=0,
f′(0)=1,
f″(0)=0,
f″′(0)=-1,
f(4)(0)=0,
…, f(2n-1)(0)=(-1)n-1,
f(2n)(0)=0.
),
…
. Вычислим
значения f(x)
и производных в точке 0:
f(0)=0,
f′(0)=1,
f″(0)=0,
f″′(0)=-1,
f(4)(0)=0,
…, f(2n-1)(0)=(-1)n-1,
f(2n)(0)=0.
Исследуем остаточный член ряда.
|Rn(x)|=
=
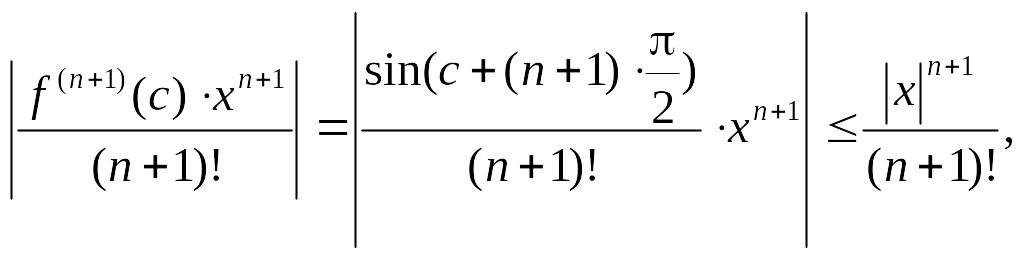 так
как |sin(c+(n+1)
|≤1.
Переходя к пределу при n→∞,
получаем
так
как |sin(c+(n+1)
|≤1.
Переходя к пределу при n→∞,
получаем
![]() следовательно,
следовательно,
![]() и
и
![]() .
Рекомендуем показать самостоятельно,
что областью сходимости ряда является
промежуток (-∞;+∞).
Таким образом, имеет место разложение
при x
(-∞;+∞):
.
Рекомендуем показать самостоятельно,
что областью сходимости ряда является
промежуток (-∞;+∞).
Таким образом, имеет место разложение
при x
(-∞;+∞):
sinx=x-
![]() . (33)
. (33)
3. Разложение функции y=cosx в ряд Маклорена. Дифференцируя ряд (33), получаем разложение при x (-∞;+∞):
cosx=1-
![]() . (34)
. (34)
4. Биномиальный ряд.
Разложим в ряд Маклорена функцию f(x)=(1+x)m, где m≠0 – любое действительное число. Для этого вычислим производные: f′(x)=m(1+x)m-1, f″(x)=(m-1)m(1+x)m-2, f″′(x)=(m-2)(m-1)m(1+x)m-3, …, f(n)(x)=(m-n+1)…(m-2).(m-1)m(1+x)m-n, … При x=0 получаем f(0)=1, f′(0)=m, f″(0)=(m-1)m, f″′(0)=(m--2)(m-1)m, …, f(n)(0)=(m-n+1)…(m-2)(m-1)m, … .
Можно показать, что областью сходимости ряда является промежуток (-1;1) (на концах интервала ряд сходится или расходится в зависимости от конкретных значений m) и что . Таким образом, при x (-1;1) имеет место разложение:
(1+x)m=1+
![]() +
+
![]() +
+
![]() +…+
+…+
![]() . (35)
. (35)
Ряд (35) называется биномиальным рядом.
5. Разложение функции f(x)=lnx в ряд Тейлора. При x=0 функция f(x)=lnx не определена, поэтому её нельзя разложить в ряд Маклорена. Разложим её в ряд Тейлора, например, по степеням (x-1). Для этого, вычислим производные: f′(x)=x-1, f″(x)=-1.x-2=-1!x-2, f″′(x)=1.2.x-3=2!x-3, f(4)(x)=-1.2. .3.x-4=-3!x-4, …, f(n)(x)=(-1)n-1. .(n-1)!x-n, … .
При x=1 получаем: f(1)=0, f′(1)=1, f″(1)=-1!, f″′(1)=2!, f(4)(1)=-3!, …, f(n)(1)=(-1)n-1(n-1)!, … .
Можно
показать, что областью сходимости ряда
является промежуток (0;2] и что
![]() .
Таким образом, при x
(0;2]
имеет место разложение:
.
Таким образом, при x
(0;2]
имеет место разложение:
lnx=
![]() . (36)
Заметим,
что разложение функций в ряды Тейлора
или Маклорена непосредственно часто
связано с громоздкими вычислениями при
нахождении производных и исследовании
остаточного члена. На примерах покажем
некоторые приёмы, позволяющие избежать
этих трудностей.
. (36)
Заметим,
что разложение функций в ряды Тейлора
или Маклорена непосредственно часто
связано с громоздкими вычислениями при
нахождении производных и исследовании
остаточного члена. На примерах покажем
некоторые приёмы, позволяющие избежать
этих трудностей.
Дифференциальные уравнения
1. Определение ду. Решение ду. Задача Коши. Общее и частное решения. Геометрический смысл уравнения
Определение обыкновенного дифференциального уравнения (ОДУ) и его решения.
Обыкновенным дифференциальным уравнением называется уравнение, связывающее между собой значения независимой переменной x, неизвестной функции y = f(x) и её производных (или дифференциалов):
![]() (1)
(все три переменные x,
y,
F
- действительны).
(1)
(все три переменные x,
y,
F
- действительны).
Опр.
Порядком
уравнения называется максимальный
порядок n
входящей в него производной (или
дифференциала).
Пример: y(4)
– y
+ x
= 0 - уравнение четвёртого порядка.
Опр.
Частным
решением
уравнения (1) на интервале (a,
b)
(конечном или бесконечном) называется
любая n
раз дифференцируемая функция
![]() ,
удовлетворяющая этому уравнению, т.е.
обращающая уравнение на этом интервале
в тождество. Так, функция y(x)
= ex
+ x
обращает уравнение : y(4)
– y
+ x
= 0 в тождество на всей числовой оси
(y(4)(x)
= ex;
ex
–(ex
+x)
+ x
= 0), т.е. является частным решением этого
уравнения. Любое уравнение порядка
,
удовлетворяющая этому уравнению, т.е.
обращающая уравнение на этом интервале
в тождество. Так, функция y(x)
= ex
+ x
обращает уравнение : y(4)
– y
+ x
= 0 в тождество на всей числовой оси
(y(4)(x)
= ex;
ex
–(ex
+x)
+ x
= 0), т.е. является частным решением этого
уравнения. Любое уравнение порядка
![]() имеет
множество частных решений (частным
решением приведённого уравнения является
и функция y(x)
= sin(x)
+ x).
Процедуру решения дифференциального
уравнения часто называют интегрированием
уравнения, при этом интегрировать
приходится в общем случае ровно n
раз, и при каждом интегрировании в
решение входит очередная произвольная
постоянная.
Опр.
Общим решением (общим интегралом)
уравнения
(1) называется такое соотношение
имеет
множество частных решений (частным
решением приведённого уравнения является
и функция y(x)
= sin(x)
+ x).
Процедуру решения дифференциального
уравнения часто называют интегрированием
уравнения, при этом интегрировать
приходится в общем случае ровно n
раз, и при каждом интегрировании в
решение входит очередная произвольная
постоянная.
Опр.
Общим решением (общим интегралом)
уравнения
(1) называется такое соотношение
![]() ;
(2)
;
(2)
что:
1. Любое решение (2)
![]() относительно
y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) - частное решение уравнения
(1);
относительно
y
(для набора постоянных C1,
C2,
…, Cn
из некоторой области n-мерного
пространства) - частное решение уравнения
(1);
2. Любое частное решение уравнения (1) может быть получено из (2) при некотором наборе постоянных C1, C2, …, Cn. Мы будем в основном рассматривать дифференциальные уравнения в форме, разрешённой относительно старшей производной:
![]() ;
(3) и получать общее решение в форме
(4)
;
(3) и получать общее решение в форме
(4)
решённой относительно неизвестной функции.
ОДУ первого порядка.
.Как следует из определения 14.1.1, обыкновенным дифференциальным уравнением первого порядка называется уравнение
![]() (5)
где
x
- независимая переменная, y(x)
- неизвестная функция. В форме, разрешённой
относительно производной, уравнение
первого порядка записывается так:
(5)
где
x
- независимая переменная, y(x)
- неизвестная функция. В форме, разрешённой
относительно производной, уравнение
первого порядка записывается так:
![]() (6)
(6)
![]() Если
пользоваться другим обозначением
производной, то можно записать (6) как
Если
пользоваться другим обозначением
производной, то можно записать (6) как
![]() (7)
(7)
Общее
решение (общий интеграл) уравнения при
n
= 1 имеет вид
![]() или
или
![]() .
Геометрический
смысл уравнения первого порядка.
Уравнение
(6) в каждой точке (x,
y)
области D,
в которой задана функция f(x,
y),
определяет
.
Геометрический
смысл уравнения первого порядка.
Уравнение
(6) в каждой точке (x,
y)
области D,
в которой задана функция f(x,
y),
определяет
![]() -
- угловой коэффициент касательной к
решению, проходящему через точку (x,
y),
т.е. направление, в котором проходит
решение через эту точку. Говорят, что
уравнение (6) задаёт в D
поле направлений. График любого решения
дифференциального уравнения (называемый
также интегральной
кривой)
в любой своей точке касается этого поля,
т.е. проходит в направлении, определяемом
полем. Интегрирование дифференциального
уравнения геометрически означает
нахождение кривых, у которых направление
касательной в каждой точке совпадает
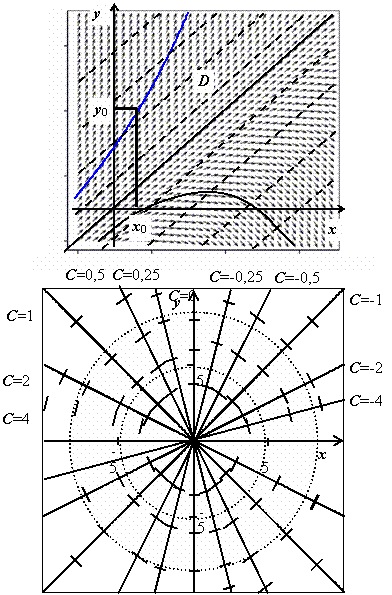
с направлением поля. На рисунке справа
изображено поле направлений, определяемое
уравнением
угловой коэффициент касательной к
решению, проходящему через точку (x,
y),
т.е. направление, в котором проходит
решение через эту точку. Говорят, что
уравнение (6) задаёт в D
поле направлений. График любого решения
дифференциального уравнения (называемый
также интегральной
кривой)
в любой своей точке касается этого поля,
т.е. проходит в направлении, определяемом
полем. Интегрирование дифференциального
уравнения геометрически означает
нахождение кривых, у которых направление
касательной в каждой точке совпадает
с направлением поля. На рисунке справа
изображено поле направлений, определяемое
уравнением
![]() ,
и три интегральные кривые (три частных
решения) этого уравнения. Решение можно
провести через любую точку области D;
единственное решение можно выделить,
если задать точку, через которую проходит
интегральная кривая:
,
и три интегральные кривые (три частных
решения) этого уравнения. Решение можно
провести через любую точку области D;
единственное решение можно выделить,
если задать точку, через которую проходит
интегральная кривая:
![]() .
Для изображения поля направлений,
задаваемого дифференциальным уравнением,
рассматривают линии уровня функции
f(x,
y),
т.е. геометрические места точек, в которых
касательные к интегральным кривым
сохраняют постоянное направление. Такие
линии называются изоклинами.
С помощью изоклин можно приближённо
изобразить интегральные кривые.
Для
примера построим изоклины уравнения
.
Для изображения поля направлений,
задаваемого дифференциальным уравнением,
рассматривают линии уровня функции
f(x,
y),
т.е. геометрические места точек, в которых
касательные к интегральным кривым
сохраняют постоянное направление. Такие
линии называются изоклинами.
С помощью изоклин можно приближённо
изобразить интегральные кривые.
Для
примера построим изоклины уравнения
![]() .
Перебираем различные значения постоянной
C,
строим линии уровня функции
.
Перебираем различные значения постоянной
C,
строим линии уровня функции
![]() ,
соответствующие этим значениям С
(т.е. прямые
,
соответствующие этим значениям С
(т.е. прямые
![]() ),
и на этих линиях ставим чёрточки в
направлении, определяемым значением С
(
),
и на этих линиях ставим чёрточки в
направлении, определяемым значением С
(![]() ,
где
,
где
![]() -
угол между чёрточкой и положительным
направлением оси Ох):
-
угол между чёрточкой и положительным
направлением оси Ох):
![]() -
ось Оу;
-
ось Оу;
![]() ;
;
![]() ;
;
![]() и
т.д. Информация о направлении интегральных
кривых, полученная из рисунка (выше
справа), достаточна, чтобы сделать
качественный вывод об их поведении:
кривые должны огибать начало координат.
Это могут быть окружности или спирали
(когда мы научимся решать дифференциальные
уравнения, мы легко установим, что это
окружности; две такие окружности
изображены пунктиром).
Задача
Коши (задача с начальным условием).
Пусть функция f(x,
y)
определена в области D,
точка
и
т.д. Информация о направлении интегральных
кривых, полученная из рисунка (выше
справа), достаточна, чтобы сделать
качественный вывод об их поведении:
кривые должны огибать начало координат.
Это могут быть окружности или спирали
(когда мы научимся решать дифференциальные
уравнения, мы легко установим, что это
окружности; две такие окружности
изображены пунктиром).
Задача
Коши (задача с начальным условием).
Пусть функция f(x,
y)
определена в области D,
точка
![]() .
Требуется найти решение уравнения
.
Требуется найти решение уравнения
(8)
удовлетворяющее начальному условию
y(x0) = y0; (9)
(начальное
условие (9) часто записывают в форме
).
Теорема
Коши (существования и решения задачи
Коши).
Если в области D
функция f(x,
y)
непрерывна и имеет непрерывную частную
производную
![]() ,
то для любой точки
в
окрестности точки x0
существует единственное решение задачи
((8),(9)).
Мы примем эту теорему без
доказательства. На самом деле для
существования решения в окрестности
точки x0
достаточно только непрерывности функции
f(x,
y);
условие непрерывности
обеспечивает
единственность этого решения. 6
,
то для любой точки
в
окрестности точки x0
существует единственное решение задачи
((8),(9)).
Мы примем эту теорему без
доказательства. На самом деле для
существования решения в окрестности
точки x0
достаточно только непрерывности функции
f(x,
y);
условие непрерывности
обеспечивает
единственность этого решения. 6
