Композиция законов распределения.

Рассмотрим распределение плотности вероятности суммы нескольких независимых случайных величин, что очень существенно для определения закона распределения общей погрешности измерений, если она складывается из небольшого числа составляющих.

Полная погрешность Δ = Δ₁ + Δ₂, причем составляющие имеют плотность распределения вероятности f₁(Δ₁) и f₂(Δ₂), плотность распределения вероятности суммы двух независимых случайных погрешностей можно записать:

Плотность распределения суммы Δ₁ и Δ₂ с нормальными законами распределения можно записать следующим образом:

,

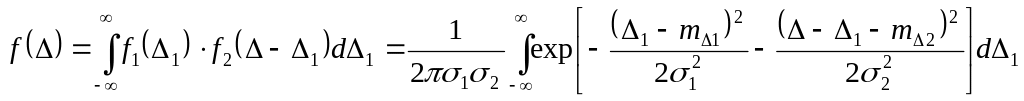где - математические ожидания и среднеквадратические отклонения погрешностей Δ₁ и Δ₂.

В результате интегрирования получается:

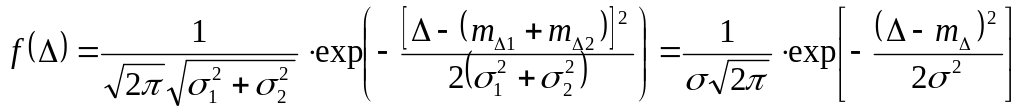
Отсюда следует, что закон распределения суммы двух независимых случайных величин распределяемый по нормальному закону также является нормальным.

Функции распределения узаконены стандартом ГОСТ 8.011-72.

Оценки истинного значения на основании ограниченного ряда наблюдения.

При бесконечном числе испытаний случайная величина может принимать любые значения, называемые генеральной совокупностью, а некоторое число n этих значений называется выборкой объем n. Определяя по этим значениям выборки характеристики закона распределения, получаем не истинные значения дисперсии и среднеквадратического отклонения, характерные для всей генеральной совокупности, а только их оценки (выборочные величины), также случайно отклоняющиеся от истинного значения.

Если истинное значение искомой величины равно , то ее оценка . Последняя является функцией, зависящей от от вида распределения случайной величины и самих результатов измерения.

Вид таких функций должен удовлетворять некоторым условиям, при которых имеет смысл принимать за наилучшее приближенное значение искомой величины ее оценку.

Способы нахождения статистических оценок для конечного ряда наблюдений и показателя их качества зависят от законов распределения.

К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования:

состоятельности;

несмещенности;

эффективности.

Состоятельной считается оценка параметра , если при увеличении числа наблюдений n она стремится (сходится по вероятности) к истинному значению оцениваемой величины, т.е. при

Несмещенной является оценка, математическое ожидание которой равно истинному значению оцениваемой величины.

Эффективной будет та оценка из нескольких возможных несмещенных, для которой оценка дисперсии будет минимальной.

В качестве оценки истинного значения принимается среднее арифметическое полученных результатов измерения:

Математическое ожидание

Несмещенными будут и другие оценки, являющиеся линейной функцией результатов наблюдения.

Среди всех рассмотренных оценок только среднее арифметическое имеет наименьшую дисперсию.

Дисперсия среднего арифметического в n раз меньше дисперсии единичного наблюдения.