2. 

3. 1.5. Производная сложной функции

4. Рассмотрим сложную функцию y = y(u(x))

5. Теорема 4. Если функции y = y(u), u = u(x) дифференцируемы (т.е. существуют производные y'_u, u'_x), тогда сложная функция y = y(u(x)) дифференцируема и y'_x = y'_u u'_x.

6. Доказательство

7. Если аргумент x получит приращение Δx, то функция u получит приращение Δu = u(x + Δx) − u(x), а функция y получит приращение Δy = y(u + Δu) − y(u). Но тогда, воспользовавшись свойствами предела функции, получаем

8. 

9. Теорема доказана.

11. 1.6. Производная обратной функции

12. Рассмотрим функцию y = f(x), для которой существует обратная функция x = g(y).

13. Теорема 5. Если обратная функция x = g(y) дифференцируема и g'(y) ≠ 0, то функцияy=f(x) дифференцируема, и 

14. Доказательство

15. Если аргумент x получит приращение Δx, то функция f получит приращение Δy = f(x + Δx) − f(x). С другой стороны, для обратной функции g приращения Δx, Δy связаны следующим образом:Δx=g(y + Δy) − g(y).

16. Тогда получаем

17. 

18. Теорема доказана. Вопрос №21

Параметрическое дифференцирование. Производные высших порядков.

Производные высших порядков

Постановка задачи. Найти производную n–го порядка функции y = f(x).

План решения

Производной n–го порядка функции y = f(x) называют производную от производной порядка (n–1), т.е.

.

1. Дифференцируем функцию y = f(x) последовательно несколько раз, пока не станет ясной формула для производной n–ого порядка.

2. Доказываем эту формулу методом математической индукции. Для этого проверяем, что она справедлива при n = 1, т.е. дает правильно , и что дифференцирование выражения для эквивалентно замене n на n+1.

Производные функции, заданной параметрически 

Вопрос №22

Понятие дифференцируемой функции в точке Х. теорема о дифференцируемой функции.

Определение Функция y=f(x) называется дифференцируемой в точке x0, если ее приращение Δy в точке x0 может быть представлено в виде: Δy=A·Δx+α(Δx)·Δx, где A -- некоторое число, независящее от Δx, а α(Δx)-- бесконечно малая функция от переменной Δx, т.е. limΔx→0α(Δx)=0.

 

Теорема Для того, чтобы функция y=f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы она в этой точке имела конечную производную. Доказательство  Необходимость. Предположим: функция дифференцируема в точке x0, т.е. Δy=A·Δx+α(Δx)·Δx. Разделив обе части данного равенства на Δx, получим: ΔxΔy=A+α(Δx). Из определения производной функции в точке: y/(x0)=limΔx→0ΔxΔy=limΔx→0(A+α(Δx))=A.

Т.е. получили, что существует конечная производная функции в точке x0 и y/(x0)=A. Достаточность. Пусть существует конечная производная y/(x0)∈R . Покажем дифференцируемость функции. y/(x0)=limΔx→0ΔxΔy.

Если функция f(x) имеет конечный предел b при Δx→0 , то ее можно представить: f(x)=b+α(x) (α(x)→0) . Исходя из этого: ΔxΔy=y/(x0)+α(Δx), где limΔx→0α(Δx)=0, Δy=y/(x0)·Δx+α(Δx)·Δx→ A=y/(x0) . Теорема доказана.

 

Вопрос №23

Понятие дифференциала, его геометрический смысл.

Формула для вычисления дифференциала.

Пусть функция y=f(x) дифференцируема на отрезке [a; b]. Производная этой функции в некоторой точке х₀  [a; b] определяется равенством

.

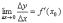Следовательно, по свойству предела

Умножая все члены полученного равенства на Δx, получим:

Δy = f '(x₀)·Δx + a·Δx.

Итак, бесконечно малое приращение Δy дифференцируемой функции y=f(x) может быть представлено в виде суммы двух слагаемых, из которых первое есть (при f '(х₀) ≠ 0) главная часть приращения, линейная относительно Δx, а второе – бесконечно малая величина более высокого порядка, чем Δx. Главную часть приращения функции, т.е. f '(х₀)·Δx называют дифференциалом функции в точке х₀ и обозначают через dy.

Таким образом, если функция y=f(x) имеет производную f '(x) в точке x, то произведение производной f '(x) на приращение Δx аргумента называют дифференциалом функции и обозначают:

dy = f '(x)·Δx

(1)

Найдем дифференциал функции y= x. В этом случае y' = (x)' = 1 и, следовательно, dy=dx=Δx. Таким образом, дифференциалdxнезависимой переменной xсовпадает с ее приращением Δx. Поэтому формулу (1) мы можем записать так:

dy = f '(x)dx

Но из этого соотношения следует, что 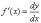 . Следовательно, производную f '(x) можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

Ранее мы показали, что из дифференцируемости функции в точке следует существование дифференциала в этой точке.

Справедливо и обратное утверждение.

Если для данного значения x приращение функции Δy = f(x+Δx) – f(x) можно представить в виде Δy = A·Δx + α, где α – бесконечно малая величина, удовлетворяющая условию 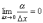 , т.е. если для функции y=f(x) существует дифференциал dy=A·dx в некоторой точке x, то эта функция имеет производную в точке x и f '(x)=А.

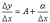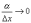Действительно, имеем  , и так как   при Δx→0, то  .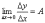

Таким образом, между дифференцируемостью функции и существованием дифференциала имеется очень тесная связь, оба понятия равносильны.

Примеры. Найти дифференциалы функций:

Если к графику гладкой функции в некоторой точке построить касательную, то, отложив на касательной такой отрезок, чтобы его проекция на ось Ох равнялась дельтаХ, получим в проекции на ось Оу отрезок, равный дифференциалу функции в точке касания.

Теорема 13. Пусть функции u = u(x), v = v(x) дифференцируемы.

Тогда