Вопрос №18

Производная функции одной переменной. Геометрическая интерпрекация. Уравнения касательной и нормаль к графику y=f(x)

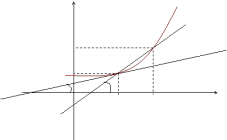
Производной функции f(x) в точке х = х₀ называется предел отношения приращения функции в этой точке к приращению аргумента, если он существует.

 

 

 у

  f(x)

 

 

  f(x₀ +x) P

  f

  f(x₀) M

 

  Пусть f(x) определена на некотором промежутке (a, b). Тогда   тангенс угла наклона секущей МР к графику функции.

 

,

где  - угол наклона касательной к графику функции f(x) в точке (x₀, f(x₀)).

 

  Угол между кривыми может быть определен как угол между касательными, проведенными к этим кривым в какой- либо точке.

 

  Уравнение касательной к кривой:   

 

  Уравнение нормали к кривой:  .

 Фактически производная функции показывает как бы скорость изменения функции, как изменяется функция при изменении переменной.

  Физический смысл производной функции f(t), где t- время, а f(t)- закон движения (изменения координат) – мгновенная скорость движения.

  Соответственно, вторая производная функции- скорость изменения скорости, т.е. ускорение.

Вопрос №19

Правила дифференцирования суммы, разности, произведения и отношения двух функций.

Если с - постоянное число, и u = u(x), v = v(x) - некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования:

1) (с) ' = 0, (cu) ' = cu';

2) (u+v)' = u'+v';

3) (uv)' = u'v+v'u;

4) (u/v)' = (u'v-v'u)/v^2;

5) если y = f(u), u = (x), т.е. y = f((x)) - сложная функция, или суперпозиция, составленная из дифференцируемых функций  и f, то 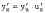 , или

;

6) если для функции y = f(x) существует обратная дифференцируемая функция x = g(y), причем 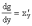   ≠ 0, то  .

Таблица производных

 

На основе определения производной и правил дифференцирования можно составить список табличных производных основных элементарных функций.

1. (u^)' =  u^1 u' ( принадлежит R¹ )

2. (a^u)' = a^u lna u'.

3. (e^u)' = e^u u'.

4. (log_a u)' = u'/(u ln a).

5. (ln u)' = u'/u.

6. (sin u)' = cos u u'.

7. (cos u)' = - sin u u'.

8. (tg u)' = 1/ cos²u u'.

9. (ctg u)' = - u' / sin²u.

10. (arcsin u)' = u' / .

11. (arccos u)' = - u' / .

12. (arctg u)' = u'/(1 + u²).

13. (arcctg u)' = - u'/(1 + u²).

Вопрос №20

Производная сложной и обратной функций. Логарифмическая производная.

ЛОГАРИФМИЧЕСКОЕ ДИФФЕРЕНЦИРОВАНИЕ

Дифференцирование многих функций упрощается, если их предварительно прологарифмировать. Для этого поступают следующим образом. Если требуется найти y' из уравнения y=f(x), то можно:

1. Прологарифмировать обе части уравнения (по основанию е) ln y = ln f(x) = j(x).

2. Продифференцировать обе части равенства, считая ln y сложной функцией от переменной x:  .

3. Выразить y' = y·j'(x) = f(x)·(lnx)'.

Примеры.

1. y = x^a – степенная функция с произвольным показателем.

.