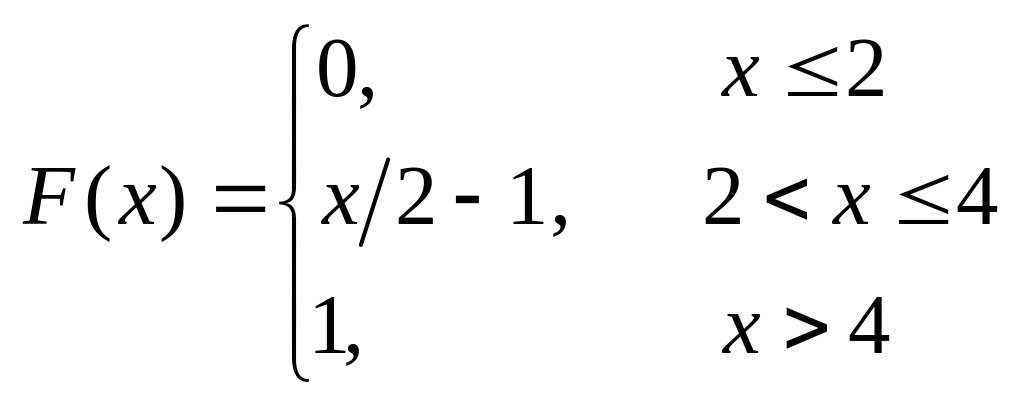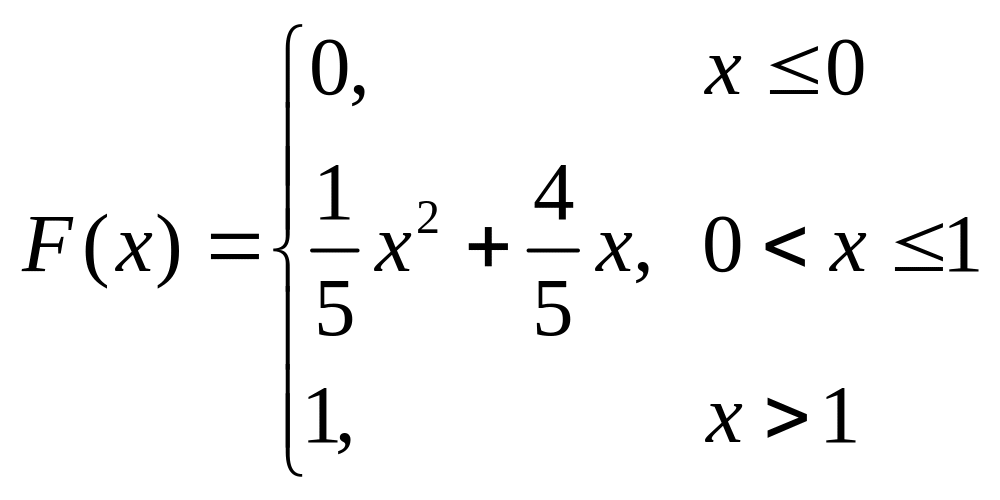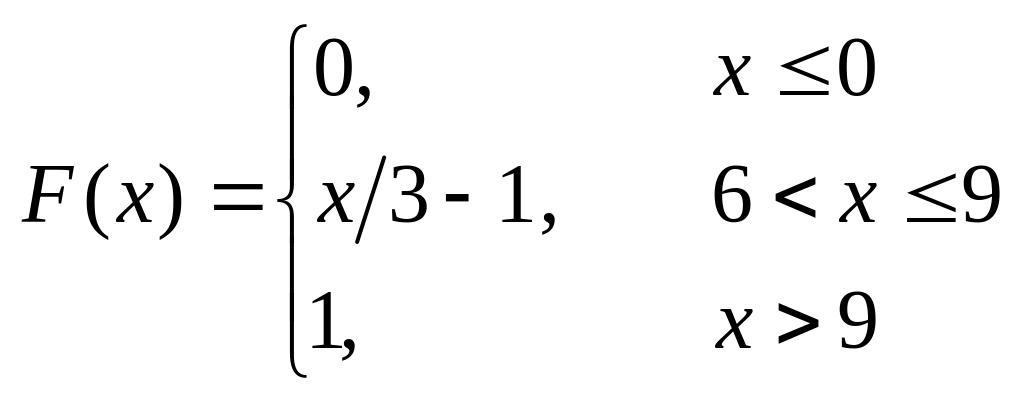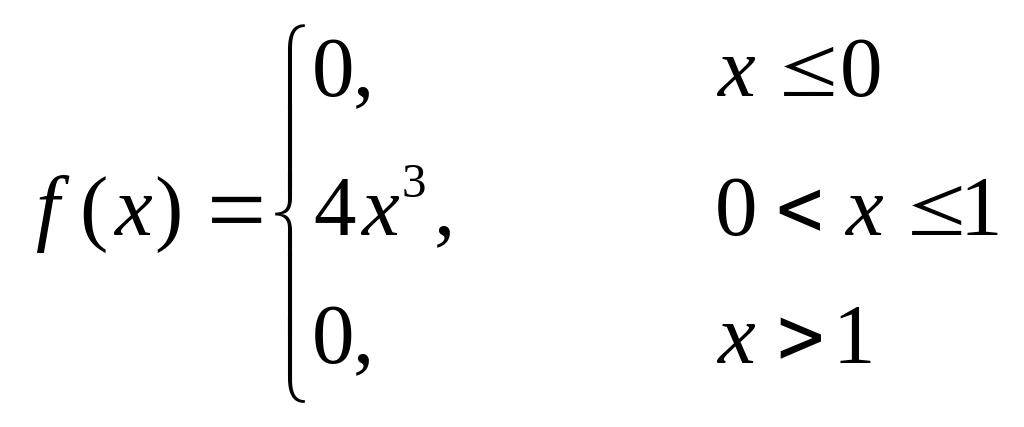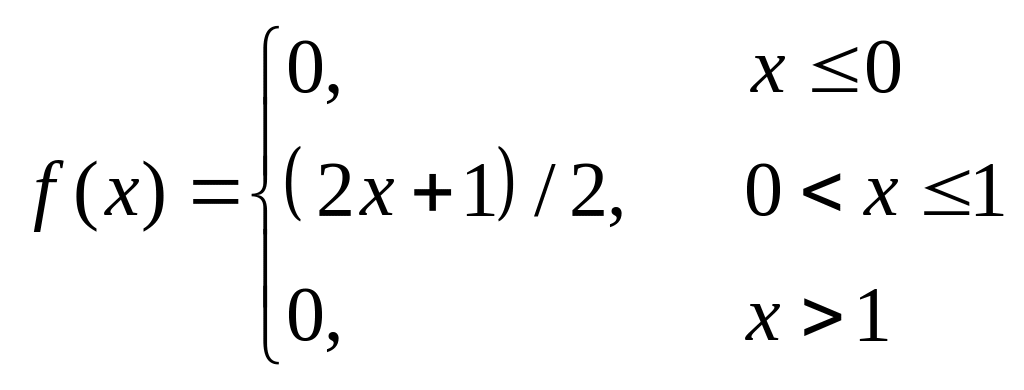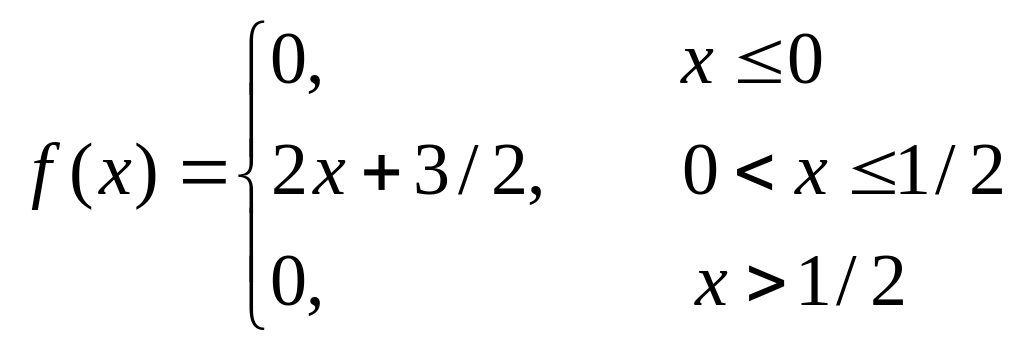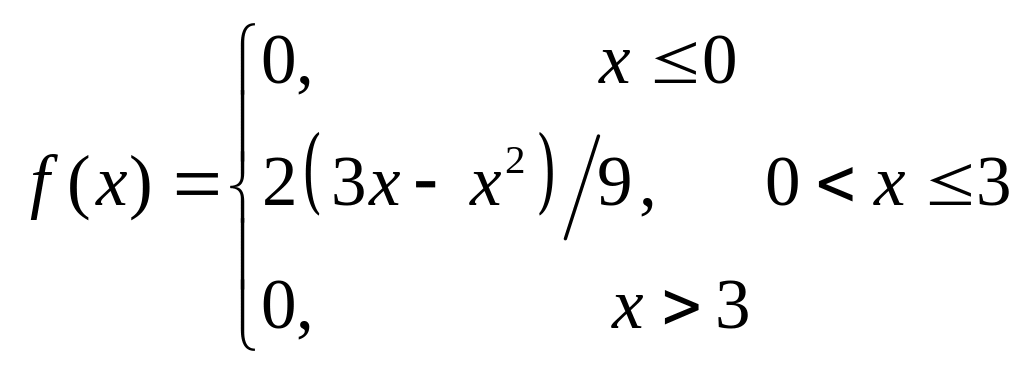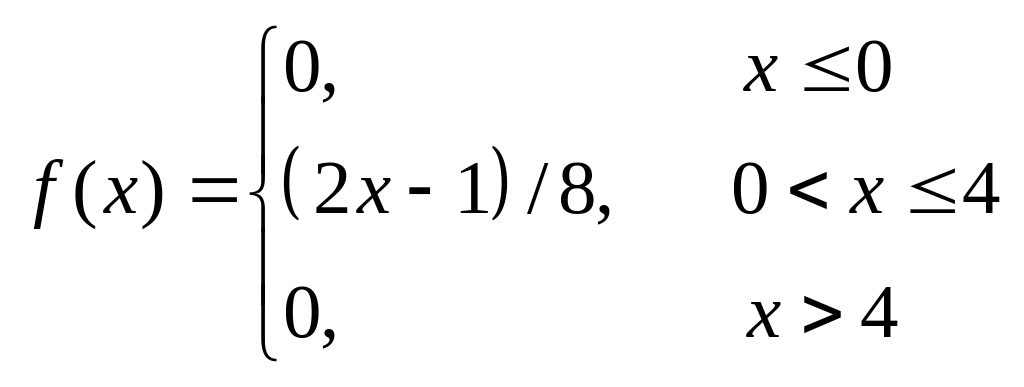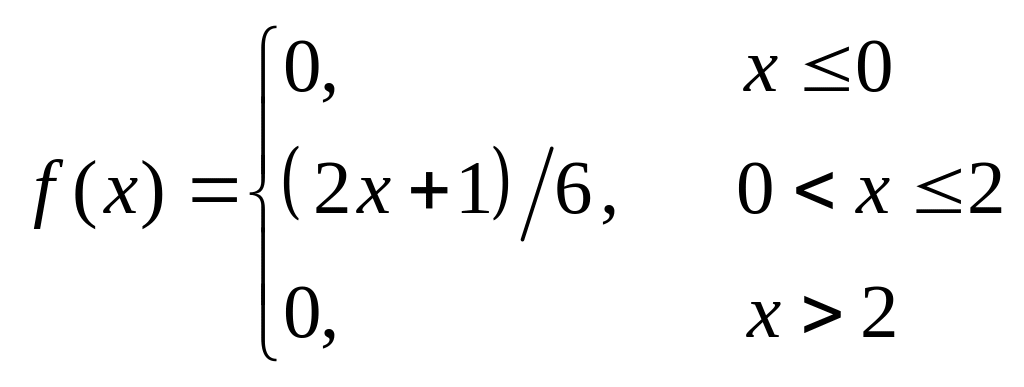6. Задачі на інтегральну та диференціальну функції розподілу

Задана інтегральна функція розподілу.

Знайти:

– диференціальну функцію ;

– математичне сподівання , дисперсію ; середнє квадратичне відхилення ;

– ймовірність попадання випадкової величини Х на інтервал ;

Побудувати графіки функцій ,

6.1		6.2		6.3
6.4		6.5		6.6
6.7		6.8		6.9
6.10		6.11		6.12
6.13		6.14		6.15

Задана диференціальна функція розподілу.

Знайти:

– інтегральну функцію ;

– математичне сподівання , дисперсію ; середнє квадратичне відхилення ;

– ймовірність попадання випадкової величини Х на інтервал ;

Побудувати графіки функцій , .

6.16		6.17		6.18
6.19		6.20		6.21
6.22		6.23		6.24
6.25		6.26		6.27
6.28		6.29		6.30

7. Задачі на закони розподілу

1. Випадкова величина Х розподілена рівномірно на відрізку [1;6]. Знайти функцію розподілу , математичне сподівання, дисперсію і середнє квадратичне відхилення величини Х.

2. Випадкова величина Х розподілена рівномірно на відрізку 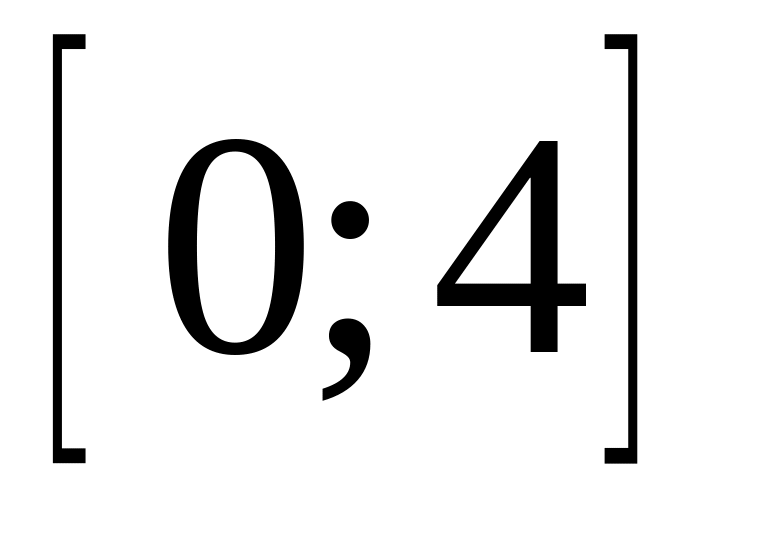. Знайти функцію розподілу, математичне сподівання і середнє квадратичне відхилення величини X.

3. Автобуси підходять до зупинки з інтервалом у 5 хв. Вважаючи, що випадкова величина Х – час очікування автобуса – розподілена рівномірно, знайти середній час очікування (математичне сподівання) і середнє квадратичне відхилення випадкової величини.

4. Математичне сподівання нормально розподіленої випадкової величини – кількості сиру, що використовується для виготовлення 100 бутербродів, – дорівнює 1кг. Відомо, що з ймовірністю 0,96 витрата сиру на виготовлення 100 бутербродів складає від 900 до 1100 г. Знайти середнє квадратичне відхилення витрати сиру на 100 бутербродів.

5. При вимірі нормально розподіленої випадкової величини виявилося, що її середнє квадратичне відхилення дорівнює 10, а ймовірність попадання цієї величини в інтервал від 100 до 140, симетричний щодо математичного сподівання, дорівнює 0,9544. Знайти математичне сподівання цієї величини і ймовірність попадання її в інтервал від 90 до 150.

6. У магазині є 20 телевізорів, з них 7 мають дефекти. Необхідно: а) скласти закон розподілу числа телевізорів з дефектами серед обраних навмання п’яти; б) знайти математичне сподівання і дисперсію цієї випадкової величини; в) визначити ймовірність того, що серед обраних немає телевізорів з дефектами.

7. Ціна розподілу шкали вимірювального приладу дорівнює 0,2. Показання приладу округляють до найближчого цілого числа. Вважаючи, що при відліку помилка округлення розподілена за рівномірним законом, знайти: 1) математичне сподівання, дисперсію і середнє квадратичне відхилення цієї випадкової величини; 2) ймовірність того, що помилка округлення: а) менше 0,04; б) більше 0,05.

8. Середній час безвідмовної роботи приладу дорівнює 80 г. Вважаючи, що час безвідмовної; роботи приладу має показниковий закон розподілу, знайти; а) щільність ймовірності і функцію розподілу; б) ймовірність того, що протягом 100 г прилад не вийде з ладу.

9. Ціна якогось цінного папера нормально розподілена. Протягом останнього року 20 % робочих днів вона була, нижче 88 гр. од., а 75 % – вище 90 гр. од. Знайти: а) математичне сподівання і середнє квадратическое відхилення ціни цінного паперу;

б) ймовірність того, що в день купівлі ціна буде знаходитися в межах від 83 до 96 гр. од.; в) з надійністю 0,95 визначити максимальне відхилення ціни цінного паперу від середнього (прогнозного) значення (по абсолютній величині).

10. Коробки з цукерками упаковуються автоматично. Їхня середня маса дорівнює 540 г. Відомо, що 5 % коробок мають масу, меншу 500 г. Який відсоток коробок, маса яких: а) менш 470 г; б), від 500 до 550 г; в) більш 550 г; г) відрізняється від середньої не більш, ніж на 30 г (по абсолютній величині?

11. Місячний доход родин можна розглядати як випадкову величину, розподілену за логнормальним законом. Вважаючи, що математичне сподівання випадкової величини дорівнює 1000 гр. од., а середнє квадратичне відхилення 800 гр. од., знайти частку родин, що мають доход: а) не менше 1000 гр. од.; б) менше 500 гр. од.

12. Систематична помилка (математичне сподівання) утримання висоти літаком +20 м, а випадкова помилка має середнє квадратичне відхилення 75 м. Для польоту літака відведений коридор висотою 100 м. Яка ймовірність того, що літак буде летіти усередині коридору, якщо його задана висота відповідає середині коридору?

13. У селищі 2800 жителів. Кожний з них приблизно два рази в тиждень їздить у місто, вибираючи дні поїздки по випадковим мотивам незалежно від інших. Випадкова величина Х – число пасажирів, що їдуть у потязі в будь-який день тижня (потяг ходить раз на добу). Знайти і .

14. Випадкова величина Х розподілена за рівномірним законом розподілу на інтервалі [0; 2]. Знайти щільність ймовірності і функцію розподілу випадкової величини X.

15. Автобуси деякого маршруту йдуть строго за розкладом. Інтервал руху 5 хв. Знайти ймовірність того, що пасажир, який підійшов до зупинки, буде очікувати черговий автобус менше 3 хв.

16. Деяка категорія людей має середню вагу 60 кг і середнє квадратичне відхилення ваги 3 кг. Визначити ймовірність того, що вага випадково взятої людини відрізняється від середньої ваги не більше ніж на 5 кг, вважаючи вагу нормально розподіленою.

17. Машина упаковує печиво в пачки по 16 штук у кожну. На етикетці робиться напис, що пачка важить 480 г. Вважається, що вага одного печива є нормальна випадкова величина з середнім 30 г і стандартним відхиленням 3 г. Покупець вибирає пачку випадково. Яка ймовірність того, що вона легше ніж 480 г?

18. Час безвідмовної роботи елемента має показниковий розподіл . Знайти ймовірність того, що за час t = 100 ч: а) елемент відмовить; б) елемент не відмовить.

19. Стрілець стріляє в мету доти, поки не влучить у неї. Знайти ймовірність влучення при одному пострілі, якщо; а) математичне сподівання числа пострілів дорівнює 5; б) дисперсія числа пострілів дорівнює 2.

20. Автоматична лінія при нормальнім настроюванні допускає бракований виріб з ймовірністю 0,001. Переналагодження лінії проводиться після першого ж виявленого ВТК бракованого виробу. Знайти середнє число всіх бракованих виробів, виготовлених між двома переналагодженнями лінії.

21. У теорії надійності технічних пристроїв, як закон розподілу часу безвідмовної роботи пристрою, часто застосовується закон Вейбулла з функцією розподілу , де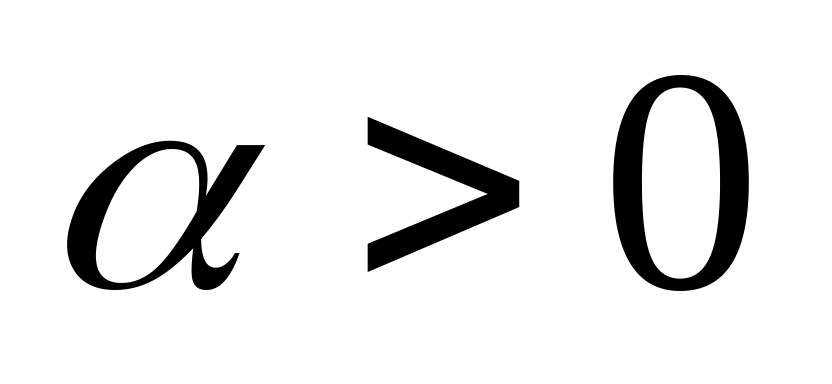 – деяка константа, – ціле додатне число. Знайти: а) щільність розподілу; б) математичне сподівання випадкової величини X, розподіленої за законом Вейбулла.

22. При досвідченій стрілянині було виявлено, що відхилення точки влучення від цілі підлягає нормальному закону з математичним сподіванням і дисперсією м². Яка ймовірність того, що <1 м?

23. При розфасовці деякої продукції пакет вважається стандартним, якщо його маса відрізняється від заданої маси 1 кг не більше ніж на 20 г (у ту або іншу сторону). Перевірено, що при акуратній роботі помилки маси підкоряються нормальному закону з математичним сподіванням і середнім квадратичним відхиленням г. Деяка партія цієї продукції з 10000 пакетів містить 9000 стандартних пакетів. Чи відповідає це даному нормальному закону?

24. Всі значення рівномірно розподіленої випадкової величини лежать на відрізку [2, 8]. Знайти ймовірність улучення випадкової величини в проміжок (3, 5).

25. Потяги даного маршруту міського трамваю йдуть з інтервалом 5 хв. Пасажир підходить до трамвайної зупинки в деякий момент часу. Яка ймовірність появи пасажира не раніше чим через хвилину після відходу попереднього потягу, але не пізніше чим за дві хвилини до відходу наступного потягу?

26. Час розформування потягу через гірку – випадкова величина, що розподілена за показниковим законом. Нехай 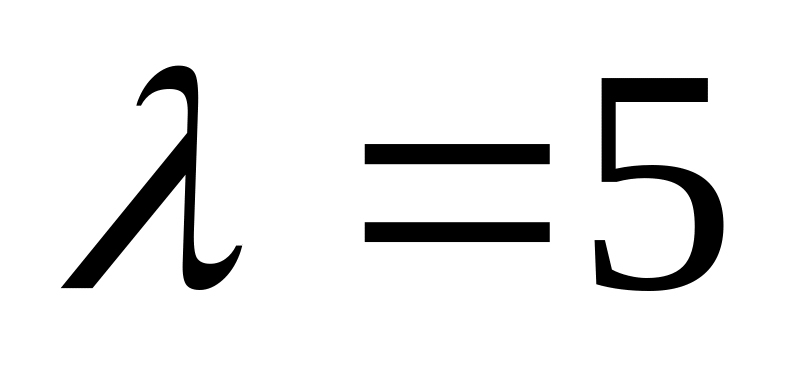– середнє число потягів, що гірка може розформувати за 1 ч. Визначити ймовірність того, що час розформування потягу: 1) менше 30 хв.; 2) більше 6 хв., але менше 24 хв.; 3) більше 0,3 г.

27. Маса вагона – випадкова величина, розподілена за нормальним законом з математичним сподіванням 65 т і середнім квадратичним відхиленням σ = 0,9 т. Знайти ймовірність того, що черговий вагон має масу не більше 70 т, але не менше 60 т.

28. Майстерня виготовляє стрижні, довжина яких являє собою випадкову величину, розподілену за нормальним законом з математичним сподіванням і середнім квадратичним відхиленням, рівними відповідно 25 і 0,1см. Знайти ймовірність того, що відхилення довжини стрижня в ту або іншу сторону від математичного сподівання не перевищить 0,25 см.

29. Потяг складається зі 100 вагонів. Маса кожного вагона – випадкова величина, розподілена за нормальним законом з математичним сподіванням т і середнім квадратичним відхиленням σ = 0,9 т. Локомотив може везти потяг масою не більше 6600 т, у протилежному випадку необхідно причіпляти другий локомотив. Знайти ймовірність того, що другий локомотив не буде потрібний.

30. Діаметр деталі, що виготовляється на верстаті – випадкова величина, розподілена за нормальним законом з математичним сподіванням а =25 см і середнім квадратичним відхиленням σ = 0,4 см. Знайти ймовірність того, що дві узяті навмання деталі мають відхилення від математичного сподівання по абсолютній величині не більш ,

16 см.