9. 4. Основные операции при построении реалистических изображений
Допустим, необходимо построить единичное изображе-ние некоторых объектов, близкое к естественному. Рассмот-рим, какие основные факторы в общем случае влияют на реалистичность изображения и каким образом они учитыва-ются при его построении.
1. Для каждого объекта должна быть создана или взята из существующих библиотек каркасная модель. Обычно, исходя из предполагаемого разрешения, для всех видов моделей производится тесселяция (tessellation) – приведение к полиго-нальному виду с треугольными гранями требуемого размера. На гранях каркасной модели должны быть заданы текстуры.
187
2. Указывается область 3-х мерного пространства с введённой на ней декартовой системой координат Охуz, в которой должно строиться изображение. Обычно эта область назы-вается сценой.
3. Объекты размещаются на сцене в требуемом положении. При этом необходимо для всех вершин каркасной модели выполнить соответствующие операции пространственных вращений, перемещений, изменений масштаба, а затем построить требуемое положение рёбер и граней.
4. На сцене размещаются источники света, а также указы-вается интенсивность рассеянного света (который обычно используется для имитации времени суток).
5. Проецирование поверхности пространственных объектов на плоскость экрана. В зависимости от удалённости и по-ложения объекта используются рассмотренные выше аксоно-метрические или перспективные проекции.
6. Отсечение - удаляются те части объектов, которые 1) не попадают в пределы экрана; 2) удалены от экрана дальше некоторого расстояния, которое определяет предел види-мости.
7. Расчёт освещения граней. Определяется количество световой энергии, которое попадает от источников на грани.
8. Удаление невидимых граней объектов. Для непрозрачных объектов грани исключают из итогового изображения в двух случаях – либо они находятся на невидимой стороне объекта, либо они закрыты гранями другого непрозрачного объекта, более близкого к наблюдателю. У прозрачных объектов производится наложение изображений граней.
9. Расчёт затенения граней – определяется отражение от их поверхности, которое должен видеть наблюдатель.
10. Постпроцессорная (окончательная) обработка. Произво-дится сглаживание стыков граней, удаление лестничного эф-фекта и т.д.
188
После последовательного выполнения описанных опе-раций изображение выводится на экран.
Данные операции могут выполняться различными мето-дами, некоторые могут опускаться и заменяться другими. Для ускорения обработки изображений применяют специальные платы – 3D ускорители, на которых часть операций, – например, матричные умножения однородных координат вершин, расчёт затенений, удаление невидимых граней, постпроцессорная обработка и др. – частично или полностью реализуются аппаратно (т.е. плата содержит специали-зированные процессоры по выполнению этих операций).
9.5. Моделирование источников освещения и расчёт освещённости малых участков поверхности объектов
В действительности объекты освещаются, как правило, одновременно многими источниками. Сочетание прямого и отражённого света создаёт сложную картину распределения тонов по поверхности объектов. В машинной графике применяют упрощённые модели как самих источников, так и расчётов падающего и отражённого от поверхности света.
Рассмотрим луч L , по которому свет распространяется в некотором направлении из источника А. Интенсивностью светового потока (интенсивностью освещения) от источника А в направлении L называют предел отношения количества лучистой энергии dE, падающей на малую площадку, перпен-дикулярную лучу L и имеющую площадь dS, к величине этой площади при dS 0 :
Рассмотрим различные модели источников.
189
1. Рассеянный естественный свет. Не имеет источника и направленности, поэтому освещает все поверхности с одина-ковой интенсивностью независимо от их ориентации в пространстве. Является обязательным компонентом реального освещения. С его помощью создаётся видимость определён-ного времени суток. При рассеянном освещении все элементы поверхностей объектов являются видимыми, однако, одина-ковая их закраска приводит к тому, что они сливаются и не проявляется рельефность объекта.
2. Точечный источник света. Свет распространяется равно-мерно во все стороны от источника, собственные размеры которого достаточно малы. Естественным аналогом является лампа накаливания. Освещённость малого участка поверх-ности dS (Рис.9.1) зависит от:
удалённости от источника;
2) ориентации её по отношению к источнику.
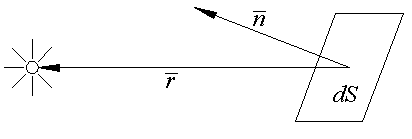
Рис 9.1
Будем рассматривать излучение энергии источни-ком, одинаковое по всем направлениям. Такое излучение называется изотропным. Обозначим вектор, соединяю-щий площадку и источник, черезr, единичную нормаль к площадке - черезn. Как следует из закона сохранения лучистой энергии в геометрической оптике, освещён-ность площадки dS , перпендикулярной векторуr, под-чиняется закону обратного квадрата расстояния:
’п = /r2.
190
Если нормальn к площадке dS расположена под некоторым ненулевым углом к векторуr, то интенсив-ность светового потока на ней подчиняется закону Лам-берта (закону косинусов):
’п*cos
(r,n)
при
cos(r
,
n)
0;
’ =
0 при cos(r , n) <0.
Учитывая одновременно оба закона геометрической оптики, интенсивность освещения площадки dS , распо-ложенной под произвольным углом к векторуr, необхо-димо рассчитывать по формулам:
(/r2)*cos (r,n) при cos(r , n)0;
’ =
0 при cos(r , n)<0;192
где – интенсивность вблизи источника,
Использование
этого реального закона геометричес-кой
оптики приводит к тому , что в получаемых
изображениях освещённость поверхностей
слишком быстро убывает с увеличением
их расстояния |r|
от источника. Поэтому на практике для
улучшения освещённости удалённых
деталей изображения освещённость
площадки рассчитывают по заменяющей
формуле
(/ (k+|r|))*cos (r,n) при cos(r , n)0;
’ =
0 при cos(r , n)<0;
где k>0 – некоторая константа, вводимая для того, чтобы при приближении к источнику ( при |r| 0) интенсивность ’ не возрастала бесконечно, ( / k ) – интенсивность вблизи источ-ника.
Данная расчётная формула только частично согласуется с законами геометрической оптики (точно учитывается лишь закон Ламберта), однако при её использовании обеспечивает-ся лучшая освещённость деталей изображенния.
191
Частными случаями точечного источника является уда-ленный источник света и конусный источник (прожектор).
Удаленный источник находится достаточно далеко от объекта (по сравнению с его размерами) в некотором фикси-рованном направлении. При этом интенсивность освещения участка поверхности объекта зависит только от его ориен-тации по отношению к направлению лучей. Обычно применя-ется для имитации солнечного освещения.
Прожектор испускает свет из заданной точки в ограни-ченном корпусе. Максимальная освещенность достигается по оси конуса, к краям уменьшается. Основное назначение - подсветка отдельных элементов изображения.
Плоский источник света. Естественным аналогом являет-ся окно. Свет излучается через плоскую фигуру преиму-щественно в направлении, перпендикулярном плоскости источника (Рис.9.2).
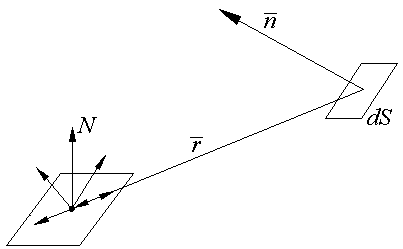
Рис. 9.2
По сравнению с точечным источником при расчёте осве-щённости требуется дополнительно учесть угол между нор-
192
малью к поверхности источникаN и радиус - вектором r.
Придавая тот же смысл величинам, входящим в формулу для точечного источника, в случае достаточно удалённых от источника объектов, получим следующую практическую формулу для расчёта освещённости малой площадки:
(
/
(k + |r|))*cos(r,n)*
cos(-r,N)
’ = при cos(r,n) 0 и cos(-r,N) 0;
0 при cos(r,n)<0 либо cos(-r,N)< 0.
Если объект достаточно близко расположен к источнику (величина |r| сравнима с его размерами), то необходимо раз-бить поверхность источника на несколько частей и рассчи-тывать освещение от них по отдельности, а затем сумми-ровать.
Объёмный источник света. Аналогом является любая до-статочно крупная (по сравнению с расстоянием |r| до объекта) оболочка, излучающая лучистую энергию во внешнее про-странство, – например, осветительные плафоны. Такие обо-лочки аппроксимируют выпуклыми многогранниками, в кото-рых каждая грань учитывается как плоский источник.