5. Аппроксимация алгебраическими полиномами

Как было отмечено ранее, аппроксимацией называет-ся такой способ моделирования объектов, при котором геометрические условия, наложенные на них, выполняются приближенно.

Р ассмотрим различные случаи аппроксимации кривых и поверхностей при помощи базиса из степенных функций _i(x)=xⁱ (i=0,1,…,n). Приближённый характер построения обусловлен: либо 1)превышением числа задаваемых гео-метрических условий над общим числом параметров синтеза либо 2) заранее обусловленным видом кривой. В первом случае в качестве критериев оптимальности прини-мают численные характеристики (равномерное и средне-квадратичное приближения). Во втором случае критерием является эстетический вид получаемого объекта (кривые и поверхности Безье).

При использовании численных критериев аппрокси-мации возможны случаи, когда при формальном превыше-нии числа геометрических условий над общим числом пара-метров синтеза возможно точное построение объекта (интерполирования). Это вызвано тем, что имеет место дублирование геометрических условий, при котором часть их является избыточной и может быть выражена через оставшиеся.

5.1. Аппроксимация по методу наименьших квадратов

Допустим, кривая y=f(x) задана на некотором отрез-ке [a,b]. Требуется линейно аппроксимировать ее в задан-ном функциональном базисе {₀(x),₁(x),…,_n(x)} суммой заданной длины n:

94

(5.1)

Критерием оптимальности в задаче аппроксимации является минимум суммы квадратов разностей (p_n(x_j) – f(x_j)) в заданных узловых точках a  x₁  x₂  … x_m  b:

(5.2 а)

П ри равномерном распределении узлов x_j в отрезке [a, b] и m   в условии (5.2 а) рассматривают усреднён-

нyю величину (а₀ , …, а_n)/m , которая в пределе стремится к интегралу

Соответственно, критерий наилучшего приближения в этом случае будет иметь вид:

(5.2 б)

Необходимым условием экстремума функции несколь-ких переменных является одновременное равенство нулю всех ее частных производных. Поэтому в обоих случаях коэффициенты a₀, a₁,…, a_n определяются из следующей системы, содержащей (n+1) уравнение:

Рассмотрим решение системы (5.3). Для дискретного критерия (5.2 а) система приводится к виду:

95

Введя матрицу А(mn) с элементами a_ks и векторb (m) с элементами b_k такими, что

условие (5.3) можно свести к системе линейных уравнений

А a = b, ( 5.4)

где a = ( a₀, a₁,…, a_n) – неизвестный вектор коэффициентов.

Решение системы:

a = A^-1b. ( 5.5)

Для непрерывного критерия (5.2 б) ход решения ана-логичен с той разницей, что в матрице А и вектореb суммы заменяются соответствующими интегралами:

Наиболее распространена аппроксимация алгебраи-ческими многочленами вида

В этом случае при непрерывном критерии аппрок-симации (5.2 б) выражения для компонент матрицы A и век- тораb находят по формулам:

9 6

А ппроксимация по методу наименьших квадратов проста в реализации, поэтому её широко применяют при об-

работке экспериментальных данных и в других случаях для построения кривых, усредняющих некоторый набор точек на плоскости.

Пример 1.

Построить по методу наименьших квадратов пря-мую, проходящую вблизи трёх точек T_i = (х_i,y_i) (i=0,1,2) c координатами (0,2) ; (1,-6) ; (2,4) . Определить по ней наи-меньшую величину среднеквадратичного отклонения _min. Найти величину среднеквадратичного отклонения  для прямой Р(х) = 0.

Решение.

1. Анализ условия. Задано 3 геометрических условия, вид искомой кривой Р₁(х) = а₀ + а₁ х, вектор неизвестных содержит 2 коэффициента: a = ( а₀ , а₁). Следовательно, необходимо выполнять аппроксимацию кривой.

2. Критерий оптимальности создаваемой кривой имеет вид:

3. Необходимые условия минимума:

Раскрывая производные, получаем систему уравне-ний относительно неизвестных коэффициентов прямой:

97

(а₀ + а₁  0 – 2) + (а₀ + а₁  1 –(-6))+ (а₀ + а₁  2 – 4)=0,

(а₀ + а₁  0 – 2) 0+ (а₀ + а₁  1 –(-6)) 1+ (а₀ + а₁  2 – 4) 2 =0.

Решение системы : а₀ = -1, а₁ = 1. Искомая прямая имеет вид: Р₁(х) = - 1 + х.

4. Величина наименьшего среднеквадратичного отклоне-ния:

 _min =(а₀ + а₁  0 – 2)²+ (а₀ + а₁  1 – (-6)) ²+ (а₀ + а₁  2 – 4) ² =

( -1 – 2)² + ( -1 + 1 +6) ² + ( -1 + 2 – 4) ² =3 ² + 6 ² +3 ² =54.

5. Величина среднеквадратичного отклонения  для прямой Р(х) = 0:

 =(0 – 2)² + (0 –(-6)) ² + (0 – 4) ² = 2 ² + 6 ² +4 ² =56.

Положение точек T₀ , T₁, T₂ и прямых Р₁(х) = - 1 + х, Р(х) =0 показано на Рис. 5.1.

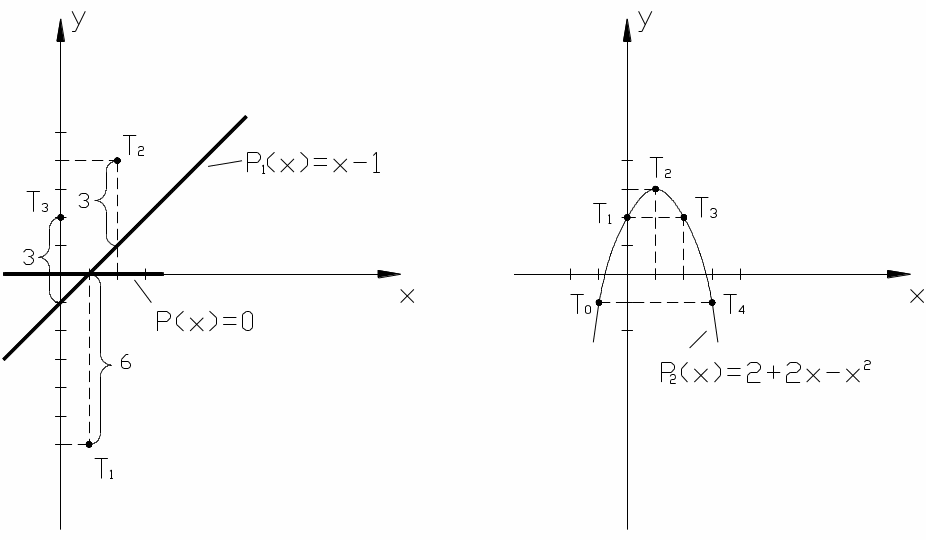
Рис. 5.1 Рис. 5.2

98

Пример 2.

Построить по методу наименьших квадратов квад-ратичную параболу, проходящую вблизи пяти точек T_i = (х_i,y_i) (i=0,1,2,3,4) c координатами (-1,-1); (0,2); (1,3); (2,2); (3,-1). Определить по ней наименьшую величину средне-квадратичного отклонения _min.

Решение.

1. Анализ условия. На кривую наложено 5 геометрических условий, общий вид искомой кривой Р₂(х) = а₀ + а₁ х+ а₂ х² , вектор неизвестных коэффициентовa = (а₀ , а₁ , а_{2 .}) со-держит три неизвестных. Следовательно, необходимо выполнять аппроксимацию кривой.

2. Критерий оптимальности создаваемой кривой имеет вид:

3. Необходимые условия минимума:

Раскрывая выражения для производных, получаем систему уравнений:

(а₀+а₁ (-1)+ а₂ (-1)²–(-1))+ (а₀+а₁ 0+ а₂ 0²–2)+ (а₀ + а₁1+ а₂  1² – 3)+ (а₀ + а₁  2 + а₂  2² – 2)+ (а₀ + а₁  3+ а₂  3² – (-1))=0,

(-1) (а₀+а₁ (-1)+ а₂ (-1)²–1)+ 0 (а₀+а₁ 0+ а₂ 0²–2)+ 1 (а₀ + а₁1+ а₂  1² – 3)+ 2 (а₀ + а₁  2 + а₂  2² – 2)+ 3 (а₀ + а₁  3+ а₂  3² – (-1))=0,

(-1) ² (а₀+а₁ (-1)+ а₂ (-1)²–1)+ 0² (а₀+а₁ 0+ а₂ 0²–2)+ 1² (а₀ + а₁1+ а₂  1² – 3)+ 2² (а₀ + а₁  2 + а₂  2² – 2)+ 3² (а₀ + а₁  3+ а₂  3² – (-1))=0.

99

Решение системы: а₀ =2; а₁ = 2; а₂ = -1.

4. Величина наименьшего среднеквадратичного отклоне-ния (для параболы Р₂(х) = 2 + 2 х - х²):

 _min =(а₀ + а₁  (-1)+ а₂ (-1)²–(-1))²+ (а₀ + а₁  0+ а₂ 0²–2)² +

(а₀ + а₁  1+ а₂ 1²–3)²+ (а₀ + а₁  2+ а₂ 2²–2)² + (а₀ + а₁  3+ а₂3²–(-1))² = 0 ²+0 ²+ 0 ²+ 0 ²+ 0 ²+0 ²=0.

Поскольку получено нулевое отклонение, то постро-ение выполнено не приближённо (аппроксимация), а точно (интерполяция). Причина заключается в том, что из 5 задан-ных геометрических условий для построения квадратичной параболы 2 являются дублирующими, т.е. задают точки на параболе, проходящей через 3 оставшиеся точки (основ-ные). Выбор основных и дублирующих точек может произ-водиться произвольно. Положение точек T₀ , T₁, T₂, T₃, T₄ и параболы Р₂(х) = 2 + 2 х - х² показано на Рис. 5.2.

Замечание. Поскольку степень n аппроксимирующей ли-нейной суммы (5.1) самим методом никак не регламентиру-ется, то её обычно задают, исходя из особенностей решае-мой задачи. Также оптимальную величину степени n мож-но определить после предварительного решения задачи для нескольких значений n и анализа полученных решений.

Метод наименьших квадратов представляет интерес и при моделировании поверхностей. Рассмотрим его приме-нение для случая степенных базовых функций, когда ап-проксимация производится при помощи квадратичной фор-мы вида

Допустим, аппроксимация производится на дискрет-ной двухмерной прямоугольной сетке (x_j , у_s ) (j =0,..., m; s =0,...,q). В узлах сетки заданы значения третьей координаты

100

z(x_j,у_s)=z_js. Квадратичная форма имеет (n+1)(p+1) неизвест-ных коэффициентов a_ik.

0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000Критерий её оптимальности имеет вид:

С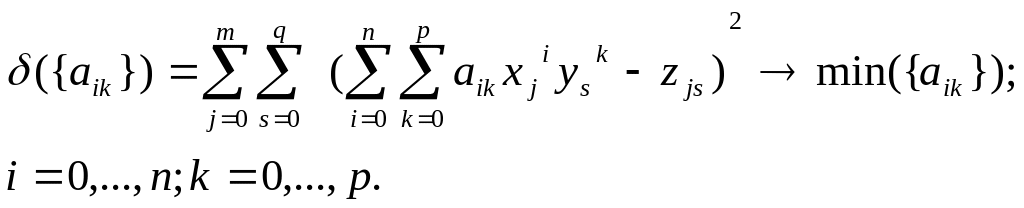 истема уравнений для определения коэффициентов a_ik аналогична (5.3):

После раскрытия выражений для производных урав-нения системы получают следующий вид:

Д анная система линейна относительно неизвестных коэффициентов a_ik . К обычному виду она приводится путём введения вместо пар индексов i,k и r,t двух линейных - I и R, которые можно взаимно-однозначно выразить через ис-ходные пары следующим образом: I(i,k) = i*n + k; R(r,t) = r*n+ t. При этом система примет вид:

Са = b, (5.8)

где С – матрица, аа и b – векторы:

0  I,R  np.

Решается система (5.8) стандартными методами.

101

В методе наименьших квадратов в качестве аппрок-симирующих могут применяться не только алгебраические полиномы, но и другие функции. Так, при обработке опыт-ных данных по долговечности точки обычно группируются вокруг положительных ветвей гипербол, которые и исполь-зуют в качестве аппроксимирующих кривых.

Задачи.

1. О чем свидетельствует нулевая величина наименьшего среднеквадратичного отклонения  _min? Ответ обосновать.

2. Допустим, необходимо построить по методу наименьших квадратов квадратичную параболу, проходящую вблизи трёх точек и определить по ней наименьшую величину среднеквадратичного отклонения . Чему равна величина _min ? Результат пояснить.

3.Построить по методу наименьших квадратов прямую, про-ходящую около трёх точек T_i = (х_i,y_i) (i=0,1,2) c координа-тами (0,0); (1,4); (2,0).Определить по ней наименьшую вели-чину среднеквадратичного отклонения _min.

4.Построить по методу наименьших квадратов прямую, про-ходящую около четырёх точек T_i = (х_i,y_i) (i=0,1,2,3) c ко-ординатами (0,0); (1,-1); (2,2) ; (3,1).Определить по ней наи-меньшую величину среднеквадратичного отклонения _min.

5.Построить по методу наименьших квадратов прямую, про-ходящую вблизи четырёх точек T_i = (х_i,y_i) (i=0,1,2,3) c ко-ординатами (0,-2) ; (1,-4) ; (2,-6) ; (3,-8). Определить по ней наименьшую величину среднеквадратичного отклонения _min. Результат пояснить.

6. Построить по методу наименьших квадратов квадратич-ную параболу, проходящую вблизи четырёх точек T_i = (х_i,y_i) (i=0,1,2,3) c координатами (0,-1); (1,-2); (2,-2); (3,2). Определить по ней наименьшую величину средне-квадратичного отклонения _min.

102