1.8. Аналитические способы задания пространственных тел

Сложные пространственные тела обычно формируют из более простых – примитивов. Для аналитического зада-ния пространственных примитивов , как правило, ис-пользуют параметрические способы. Поскольку такие примитивы являются трёхмерными объектами (3d-объек-тами), то у них необходимо задавать области изменения трёх независимых параметров.

Если объект близок по форме к параллелепипеду, то для его задания наиболее удобной является декартова система координат. В случае примитивов, близких по форме к цилиндру или сфере, применяются, соответственно, цилиндрическая и сферические системы координат.

1.9. Основные операции с графическими примитивами

1. Определение пересечения (параллельности, наложения) плоских прямых (лучей, отрезков).

Заданы две плоские прямые , :

; .

Необходимо выяснить, имеет ли место пересечение, парал-лельность или наложение данных прямых. В случае пере-сечения – найти значения параметров прямых в точке пересечения.

Условие пересечения имеет вид , где - значения параметров u, v в точке пересечения. Перейдя к единичным направляющим векторам и новым параметрам ; , условие представим в виде:

где .

Для упрощения анализа рассматриваем также матрицу .

Возможны следующие случаи:

1. det 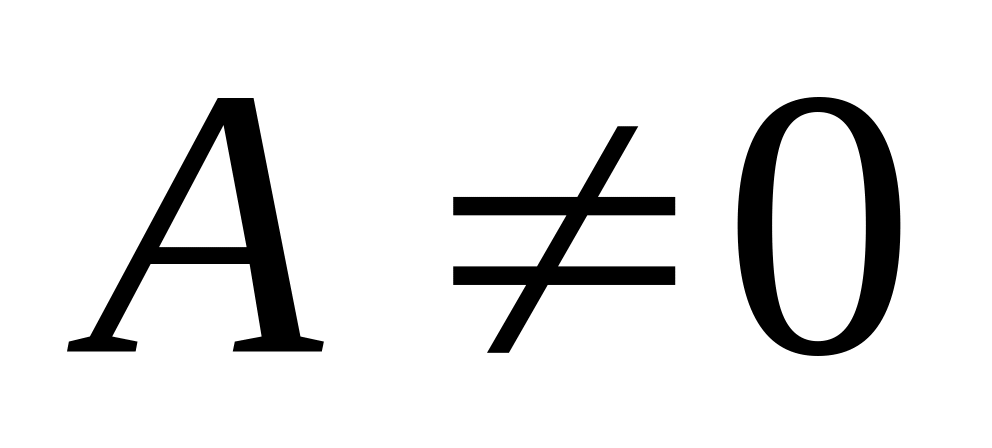. При этом прямые пересекаются. Значения параметров u, v в точке пересечения

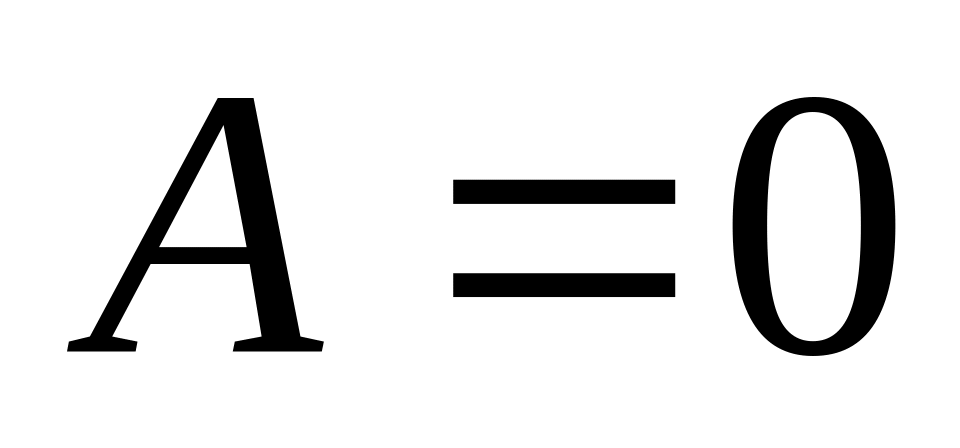2. det , det 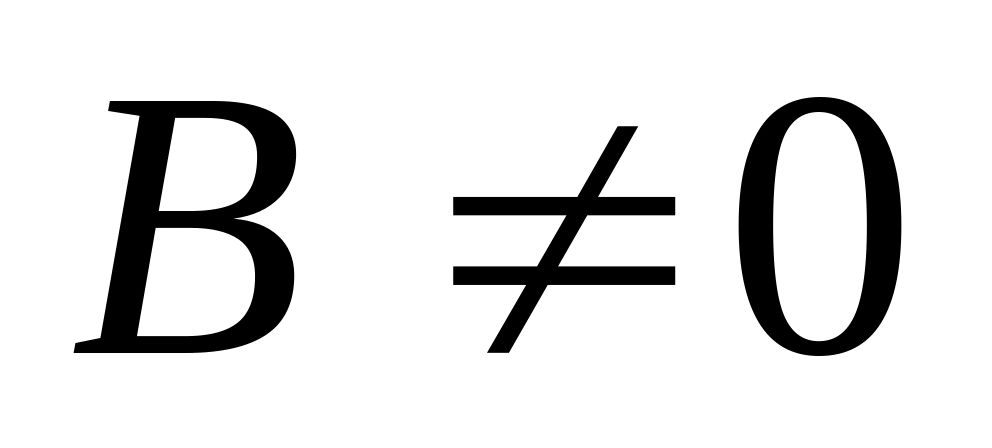. Прямые параллельны.

3. det , det . Прямые накладываются друг на друга.

Если рассматривается пересечение лучей (отрезков) то дополнительно к условию 1 необходимо проверять условия либо .

2. Расчёт пересечения (перекрещивания, параллельности, наложения) пространственных прямых (лучей, отрезков).

Как и в п.1, представим условие пересечения в виде

, где А=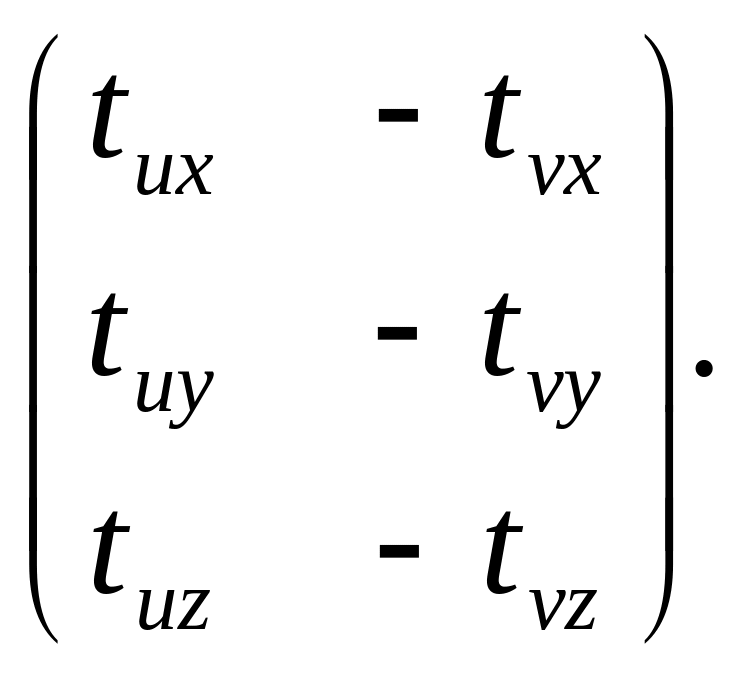

Обозначим подматрицы А следующим образом:

; .

Также рассмотрим матрицы

; .

Возможны следующие ситуации:

I. . Прямые не параллельны.

1) Если , то рассчитываем значения параметров в возможной точке пересечения по формуле:

.

Подставляем полученные значения параметров в условие . Рассматриваем варианты:

а) условие выполнено. Следовательно,L₁(u) иL₂(v) пересе-каются при значениях , .

б) условие не выполнено. Тогда прямые скрещиваются.

2) Если , то рассчитываем

и аналогично проверяем условие .

II. . Возможны 2 варианта :

а) . В этом случае имеет место наложе-ние прямых, т.е. они совпадают.

б) . Прямые параллельны и не име-ют общих точек.

3.Определение пересечения (касания) дуги окружности С с прямой L (отрезком )на плоскости.

Задана дуга окружности С:

.

(в случае полной окружности )

и прямаяL, проходящая через точки , :

L(u) =P₁+ (P₂ -P₁ ) u ; (в случае отрезка 0  u  1).

Необходимо выяснить, пересекаются (касаются) ли эти примитивы, если да – то найти координаты точки пере-сечения (касания) и указать соответствующие значения па-раметров и u .

Вначале проверяем расстояние от центра P₀ дуги С до прямойL. Для этого вначале определим точку P_n , в которую опускается перпендикуляр из наL. Так как P_n L, то ей соответствует некоторое значение параметра прямой u_n, для которого справедливо: .

Из условия перпендикулярности отрезков и , записанного как равенство нулю скалярного произведения: ,

получим: .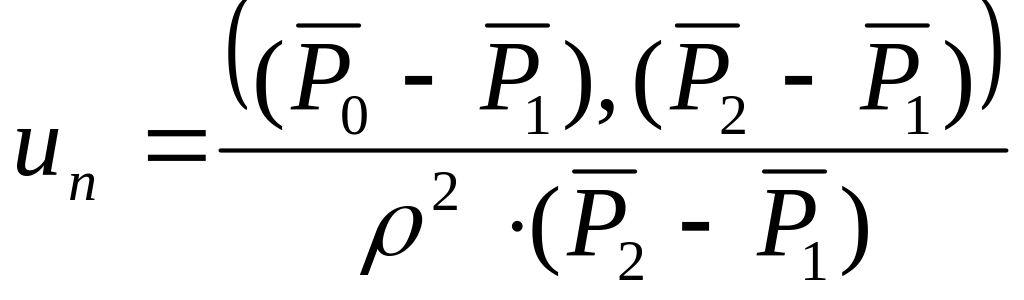

По находим и длину перпендикуляра . Затем проверяем: .

Если условие не выполняется, то пересечение заведо-мо невозможно и ответ отрицательный. Если условие вы-полняется, то возможны две ситуации:

1. ( Рис.1.11). Определим две возможных точки пересечения L с окружностью и . Для этого вначале рассчитываем расстояния а от точек и до основания перпендикуляра :

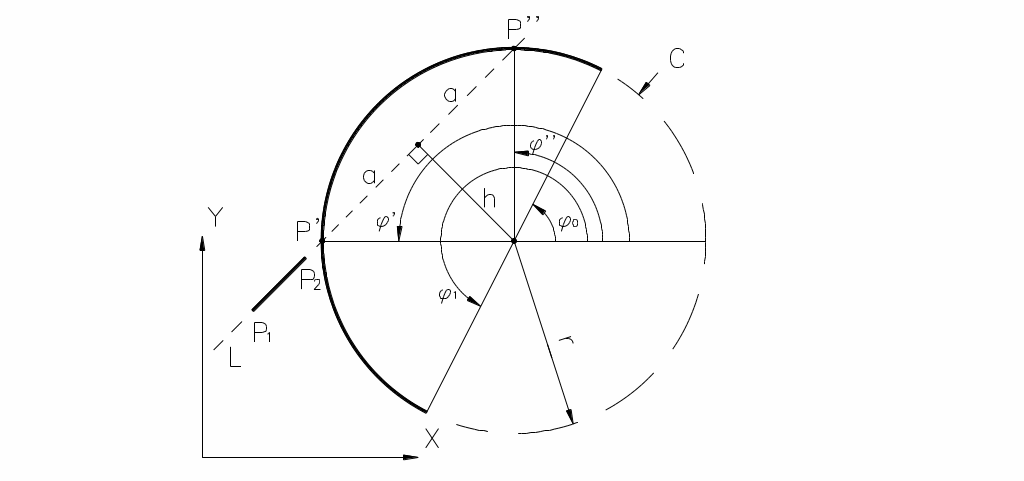
Рис. 1.11

Затем, используя единичный направляющий вектор t прямойL, находим координаты возможных точeк пересе-чения: ; .

Углы и ,соответствующие и , находим по (1.8 б, в). Если , то прямая L пересекает дугу C в точ-ке . Аналогично проверяем для .

В том случае еслиL - отрезок (луч), то дополнительно определяются значения параметра u в точках и :

; ,

а также проверяются условия:

, .

Если условия выполнены, то пересечение есть, иначе – нет.

2. . Возможно касание в точке (Рис.1.12).

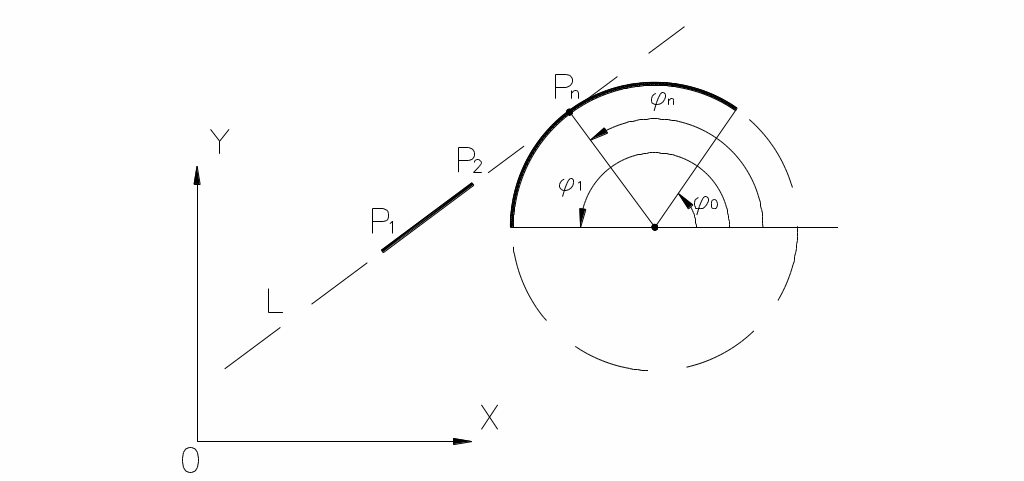
Рис. 1.12

По формулам (1.8 б,в) определяем _п. Если₀  _п ₁, то касание с дугой есть. Иначе – нет.

Для отрезка (луча) дополнительно проверяется усло-вие 0  u _п  1 (0  u _п < + ).

4.Расчёт пересечения (касания) дуг окружностей , .

Заданы дуги окружностей

;

.

Необходимо выяснить наличие пересечения (касания) и . Если оно есть, то указать координаты точек пере-сечения (касания) и соответствующие им значения пара-метров и .

Находим расстояние между центрами окружнос-тей и и проверяем выполнение условия ₁₂  r₁ + r₂.

Если условие не выполнено, то пересечения заведомо нет, так как расстояние между центрами окружностей боль-ше суммы их радиусов.

Если условие выполнено, то есть 2 возможности.

1. ₁₂ = r₁ + r₂. Касание окружностей, содержащих дуги и (Рис 1.13). Рассматриваем вектор и определяем по

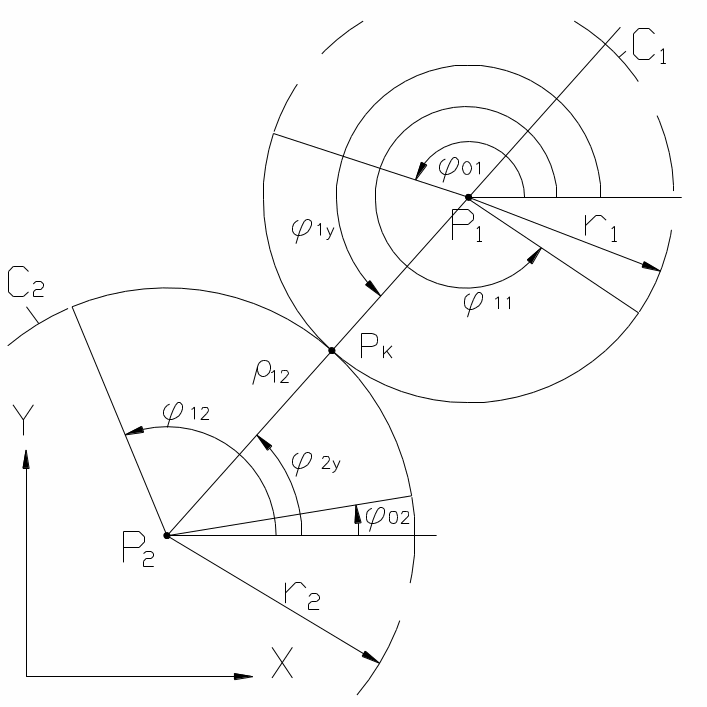
Рис. 1.13

(1.8.б, в) угол его наклона относительно оси х. Затем рассчитываем угловое положение точки касания для второй окружности: (mod 2).

Если и , то касание есть. Декартовы координаты точки касания:

.

Если хотя бы одно из условий не выполняется, то каса-ния нет.

2. ₁₂  r₁+r₂ . Пересечение окружностей, содержащих и

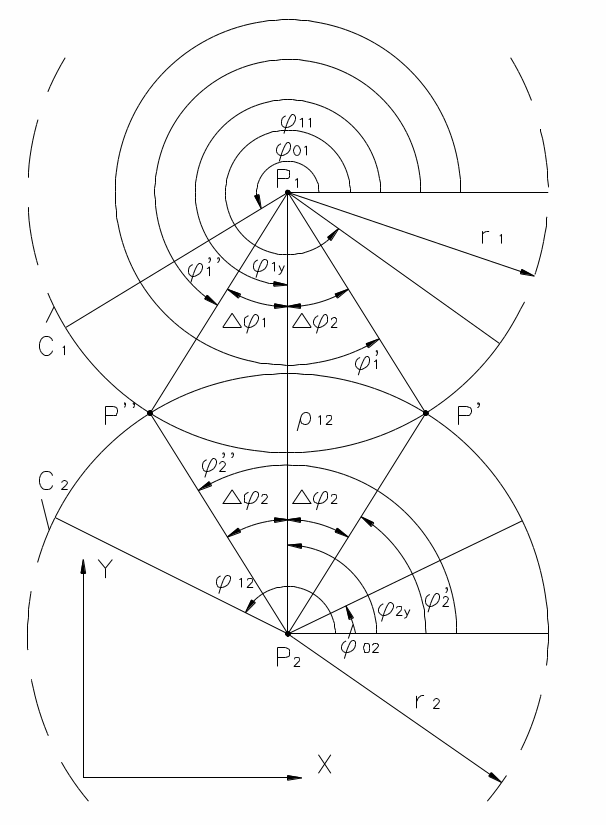
Рис. 1.14

(Рис 1.14). Как и в п.1, находим угол .Угловое отклонение точек пересечения на первой окружности от угла находим по теореме косинусов:

.

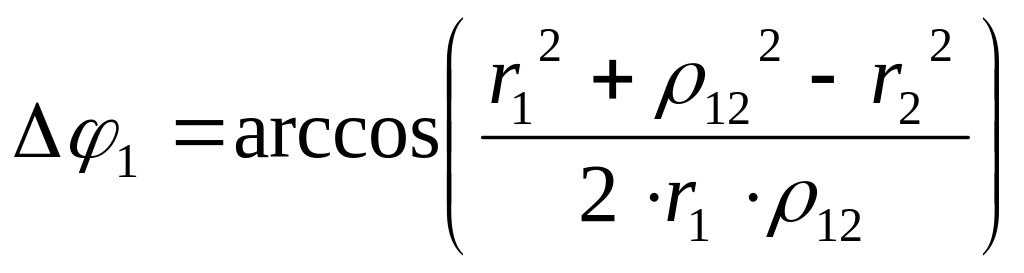Угловое положение точек пересечения и на окружности, содержащей , задается углами

,

.

Условие принадлежности точек и дуге имеет вид:

, .

Проверка принадлежности точек и дуге производится аналогично:

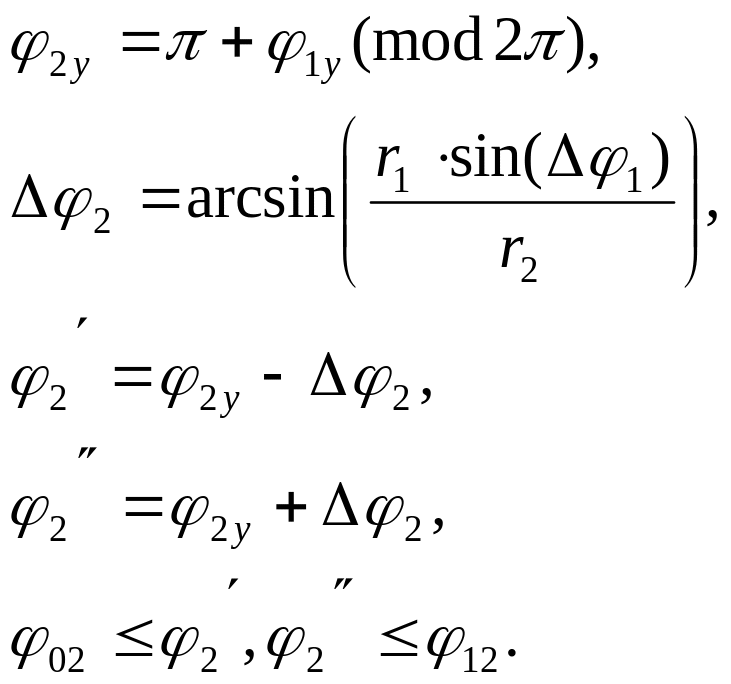
Точка является точкой пересечения дуг, если для нее одновременно выполняются оба условия.

5.Определение пересечения ( параллельности, наложения ) пространственной прямой ( луча, отрезка ) , проходя-щей через точки Р₁ , Р₂ , и плоскости (,w) (пространст-венного треугольника),проходящих через точки Р₃ , Р₄ , Р₅ .

Уравнение прямой:

;

Уравнение плоскости:

; , .

В точке пересечения . Заменяя век-торные разности (Р₂ –Р₁), (Р₄ –Р₃), (Р₅ –Р₃) соответ-ствующими единичными направляющими векторами , , :

=(Р₂ –Р₁)/Р₂ –Р₁,

= (Р₄ –Р₃)/Р₄ –Р₃,

= (Р₅ –Р₃)/Р₅ –Р₃,

и вводя новые параметры:

; ; ,

условие пересечения можно представить в ви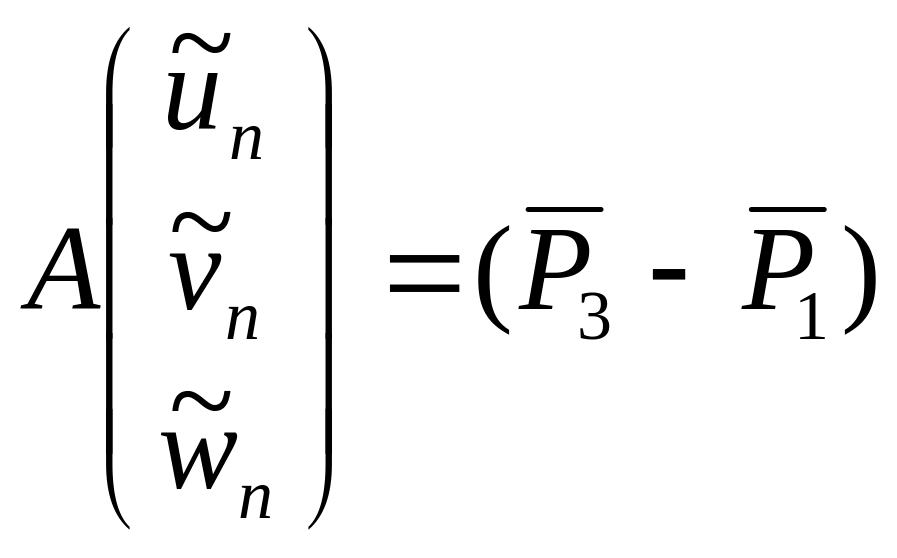де:

, где

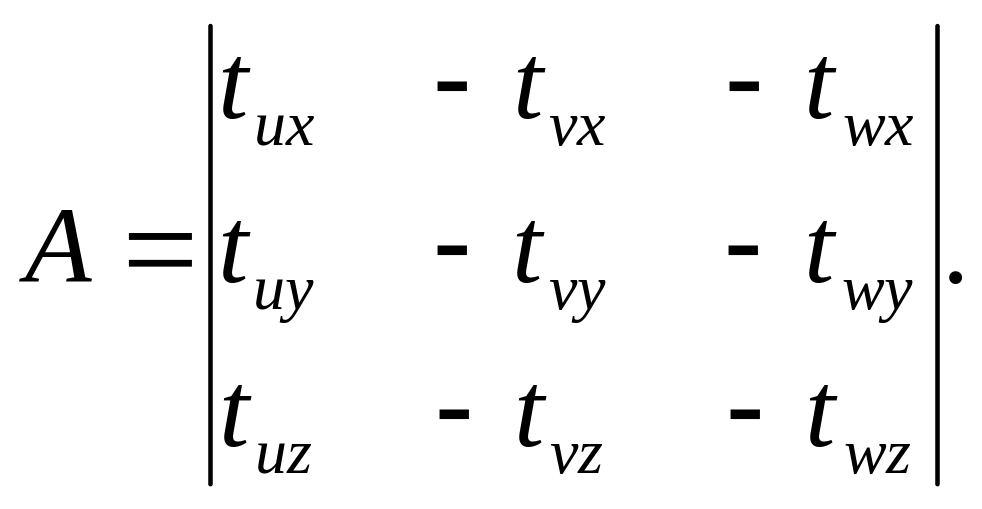
Возможны следующие случаи:

1. det A=0, P₃ -P₃=0 - наложение прямой на плоскость .

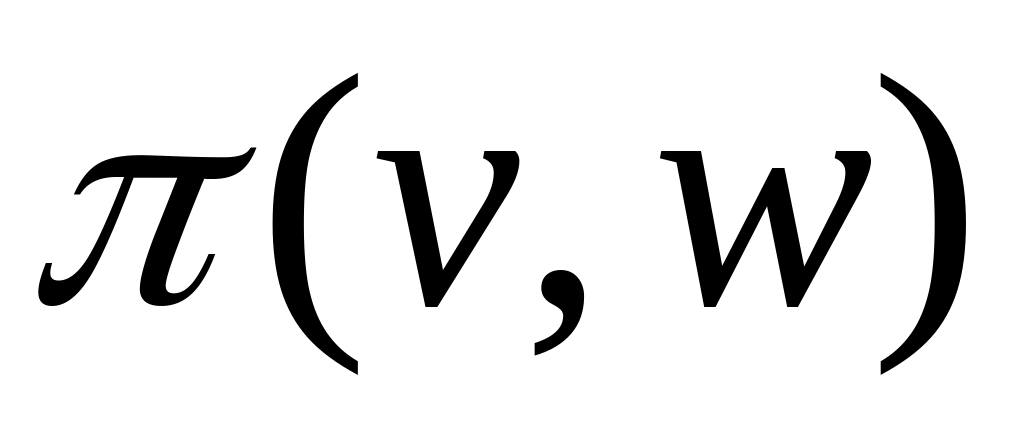2. det A=0, P₃ -P₃0 - прямая параллельна , точек пересечения нет.

3. det A  0 - прямая пересекает . Значения параметров в точке пересечения

.

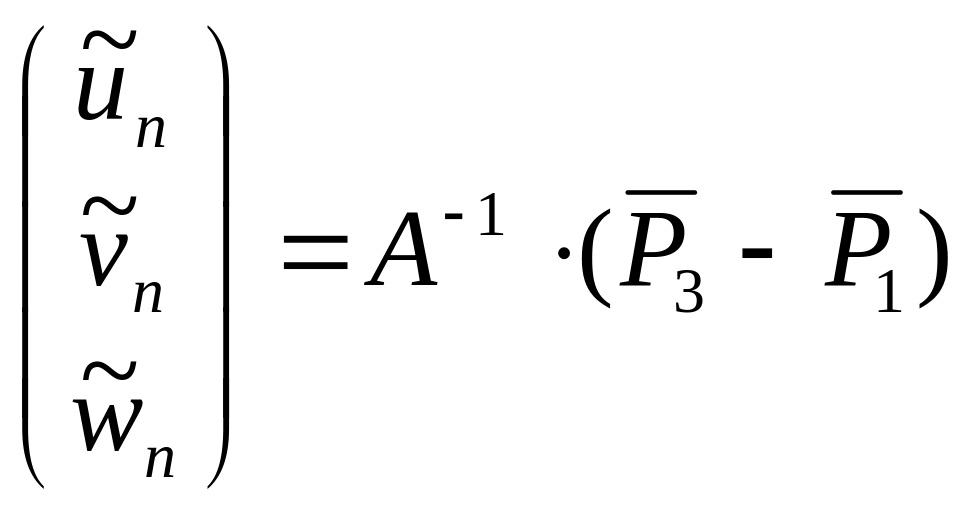В том случае, если примитив L(u) является отрезком (лучом), то дополнительно проверяется условие на параметр u_n: 0  u_n  1 ( 0  u_n < +).

Если (,w) является пространственным треугольни-ком, то необходимо проверить дополнительные условия на параметры v _n и w _n:

0  v_n , w _n  1,

0  v_n+ w_n  1.

6. Расчёт площади плоских многоугольников.

Обычно в машинной графике плоский n - угольник за-дают при помощи декартовых координат его вершин (х_i , у_i),(i = 1,…,n). Наиболее просто площадь S многоугольника рассчитывается по формуле