П ример 2 .Уравнение конуса второй степени

Вершиной является начало координат (0,0,0) (Рис.1.9).

3. Алгебраические поверхности порядка n. К ним от-носят поверхности, уравнения которых могут быть пред-ставлены в алгебраической форме степени n.

а) Алгебраические поверхности 1 порядка

а₁ х + а₂ у + а₃ z + а₄ = 0

при а₁²+ а₂²+ а₃²  0 . (1.14)

Уравнение задаёт плоскость в 3-мерном пространстве.

б) Алгебраические поверхности 2 порядка.

а₁₁х²+а₂₂у²+а₃₃z²+2а₁₂хz+2а₁₃xz+2а₂₃yz+

2а₁₄х+2а₂₄у+2а₃₄z+а₄ =0

при а₁₁²+а₂₂²+а₃₂²+а₁₂²+а₁₃²+а₂₃²0. (1.15)

В зависимости от значений коэффициентов уравнение может описывать следующие поверхности:

1) эллипсоид (Рис. 1.5);

2) параболоид (Рис. 1.6);

3) гиперболоид;

4) цилиндр (Рис. 1.8);

5) конус (Рис. 1.9).

4.Трансцедентные поверхности.

Такими являются поверхности не представимые в ал-гебраическом виде.

Пример 3. sin(xy) + z = 0.

1.7. Основные способы задания плоскостей

1. Канонический вид.

ax+by+cz+d=0 . (1.16)

2. Плоскость, проходящая через заданную точку Po (xo, yo, zo) перпендикулярно векторуv = (a, b, c). Условие перпен-дикулярности имеет вид: (PP₀,v) = 0. Раскрывая скаляр-ное произведение, получим: a (x-x₀) + b (y-y₀) + c (z-z₀) + d = 0. В каноническом виде: ax + by + cz + d = 0, d = - ax₀ - by₀ - cz₀ .

3. Нормальная форма. Может применяться для плоскостей, не проходящих через начало координат. Уравнение имеет вид:

xcosα + ycosβ + zcosγ –P = 0, (1.17)

где Р - модуль перпендикуляра N, опущенного из начала ко-ординат (0,0,0) на рассматриваемую плоскость,

α, β, γ – углы вектора N с осями x, y, z.

Допустим, плоскость задана в каноническом виде и необходимо выразить ее в нормальной форме. Для коси-нусов углов α, β, γ справедливо условие

cos²α + cos²β +cos²γ = 1.

Оно будет всегда выполнено в выражении (1.16), если все его слагаемые умножить на нормирующий множитель .

Модуль нормали при этом будет следующим:

4. Плоскость, проходящая через три точки P₀(x₀,y₀,z₀), P₁(x₁,y₁,z₁), P₂(x₂,y₂,z₂), не лежащие на одной прямой. Если обозначить координаты текущей точки плоскости через P=(x, y, z), то условие принадлежности векторов P₁P,P₁P₂,P₁P₃ одной плоскости сводится к равенству нулю их смешанного произведения:

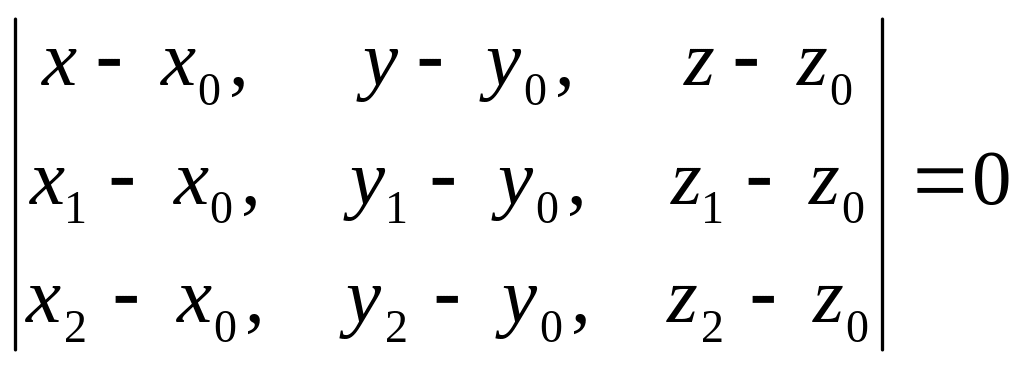
(1.18)

5. Параметрическое задание плоскости, проходящей через три точки P₁(x₁,y₁,z₁), P₂(x₂,y₂,z₂), P₃ (х₃,y₃,z₃) . Рассмотрим пространственный треугольник, заданный точками {P_j}={P₁,P₂,P₃} (Рис. 1.10).

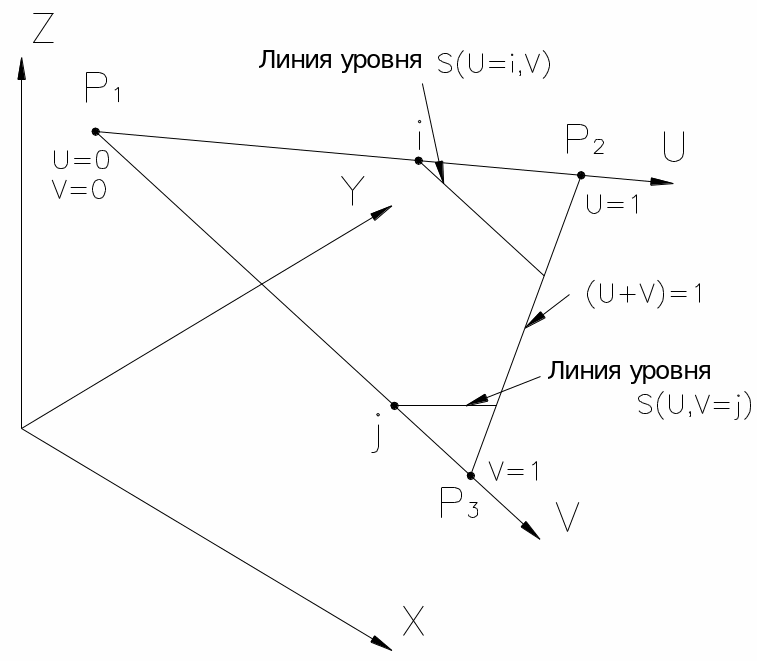
Рис. 1.10

Параметры u и v введем так, чтобы они образовывали на плоском треугольнике как бы локальную систему коор-динат. Начало её в точкеP₁ , ось u направлена отP₁ кP₂ , ось v - отP₁ кP₃ . Значения u и v нормированы таким образом, что в точкахP₂ иP₃ они принимают значение, равное 1. Математическое задание координат точек, лежа-щих на сторонах и внутри треугольника, имеет вид:

S(u,v)= P₁  (1-u-v) +P₂  u +P₃  v, (1.19)

при ограничениях на параметры: u + v  1; u, v  0.

В вершинах треугольника:S (0,0)=P₁; S(1,0)=P₂; S(0,1)=P₃ .

Для визуализации поверхностей на них проводят ли-нии уровня, которые задаются уравнениями:

S(u,v=const) – линия соответствующая уровню v;

S(u=const,v) – линия соответствующая уровню u.

Единичные нормали к треугольнику, заданному тре-мя точками, проще выразить с помощью направляющих векторов и . Из условий перпендикулярности с , :

;

получаем два возможных решения

где

; ; .

Нормаль образует правую тройку с , , - левую.

Плоскость, проходящая через , , , задается аналогично треугольнику с той разницей, что - < u,v <+. Направляющие векторы и нормали к ней определяются аналогично.