
- •Введение
- •I. Основные виды геометрических объектов в машинной графике
- •1.1. Основные аналитические способы задания кривых
- •3. Параметрический способ задания. В качестве независимой переменной выбирается некоторый параметр t. Все координаты точек на кривой выражаются через него:
- •1.2. Виды кривых
- •1.3. Основные способы задания прямых
- •1.4. Способы задания окружностей и их дуг
- •Углы 0 , 1 находим, как и в п. 2 , по формулам (1.8 б, в).
- •1.5. Основные аналитические способы задания поверхностей
- •1.6. Виды поверхностей
- •П ример 2 .Уравнение конуса второй степени
- •1.7. Основные способы задания плоскостей
- •1.8. Аналитические способы задания пространственных тел
- •1.9. Основные операции с графическими примитивами
- •Как и в п.1, представим условие пересечения в виде
- •1.10. Параметрические кривые и их построение в векторном виде
Углы 0 , 1 находим, как и в п. 2 , по формулам (1.8 б, в).
4. По начальной
точке TН(xН,yН),
углу наклона касательной в ней
![]() и конечной точке TК(xК,yК)
(Рис.1.4).
и конечной точке TК(xК,yК)
(Рис.1.4).
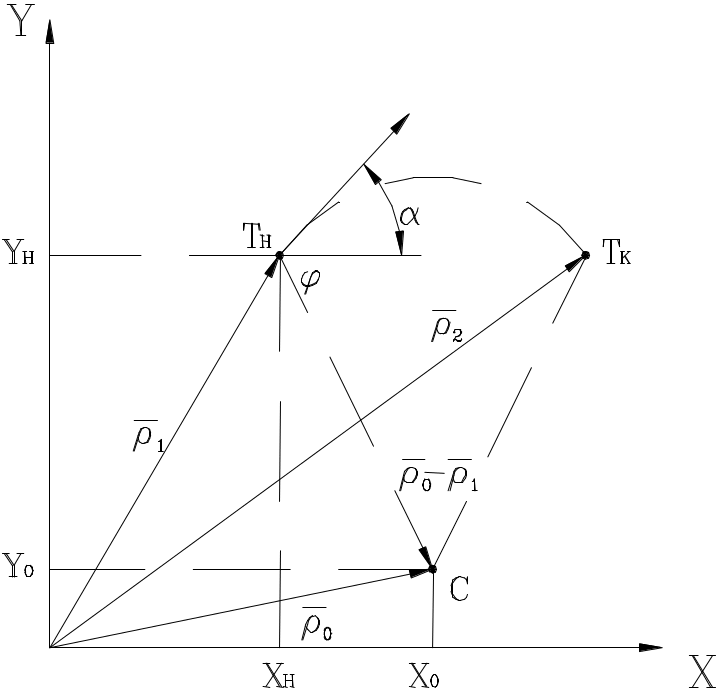 Рис.
1.4
Рис.
1.4
Введя направляющий
векторt=(cos,sin)
в точке TН, представим
систему уравнений для определения
вектора
![]() в виде:
в виде:
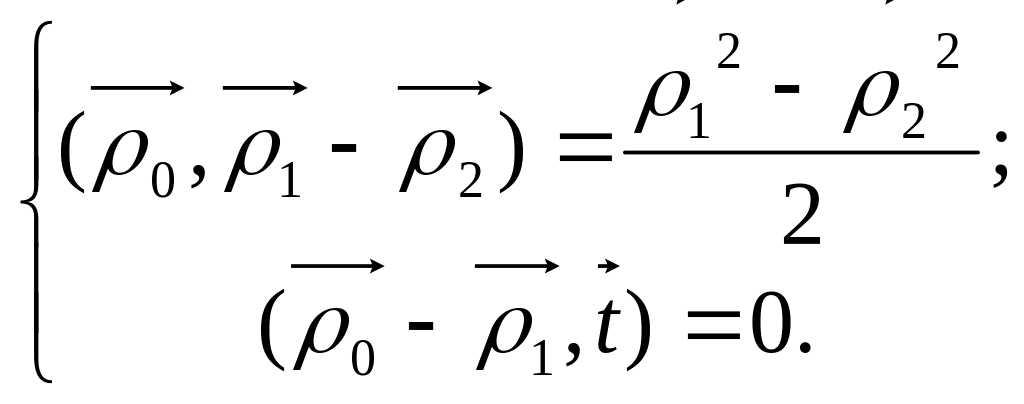
Общее решение ее имеет вид:
![]() ,
,
где
![]() - нормаль к
- нормаль к
![]() ,
,
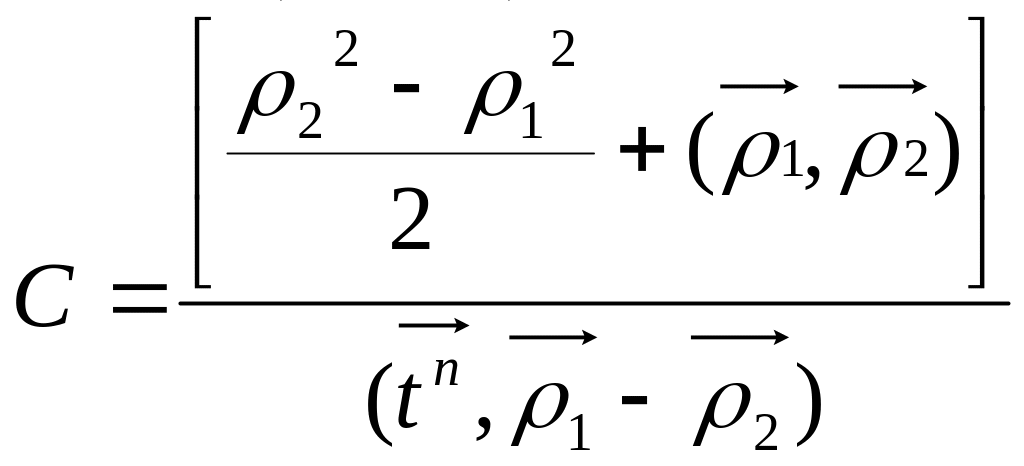 .
.
Отсюда получим:
![]()
Радиус r,
углы
![]() находим так же, как и в п. 2.
находим так же, как и в п. 2.
1.5. Основные аналитические способы задания поверхностей
1. Неявный способ задания. Применяется в тех случа-ях, когда ни одну из координат нельзя однозначно выразить через другие. Уравнение можно представить в виде:
f (x, y, z) = 0. (1.9)
Если область изменения координат (x, y, z) меньше об-ласти решений уравнения (1.9), то её указывают дополни-тельно. В случае совпадения область изменения обычно не указывают.
Пример 1. Уравнение эллипсоида с полуосями (a,b,c) и центром в начале координат (Рис. 1.5):
![]()
 Точками
эллипсоида являются все возможные
реше-ния данного уравнения.
Точками
эллипсоида являются все возможные
реше-ния данного уравнения.
Рис. 1.5 Рис. 1.6
2. Явный способ задания. Одна из трёх координат ана-литически выражается через остальные. Например, коорди-наты точек по оси z выражаются через координаты по осям x, y:
z = f(x,y). (1.10)
Если аргументы принимают любые вещественные значения, то область их изменения можно не указывать.
Пример 2.
![]() -
параболоид вращения вокруг оси z
с вершиной в начале координат (0,0,0)
(Рис. 1.6).
-
параболоид вращения вокруг оси z
с вершиной в начале координат (0,0,0)
(Рис. 1.6).
3. Параметрический способ задания. Координаты то-чек поверхности являются функциями двух параметров (u,v):
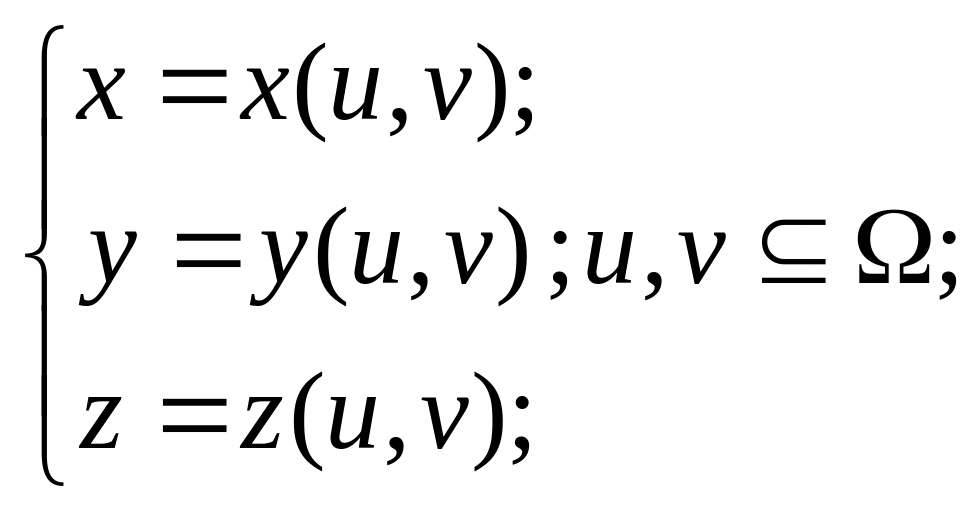 (1.11)
(1.11)
где - область изменения независимых параметров u, v .
Пример 3.
x = 3 u + 5 v + 9 (1 – u - v);
y = 2 u +7 v + 10 (1 – u - v);
z = 1 u + 6 v + 11 (1-u-v);
0 u , v 1; 0 u +v 1.
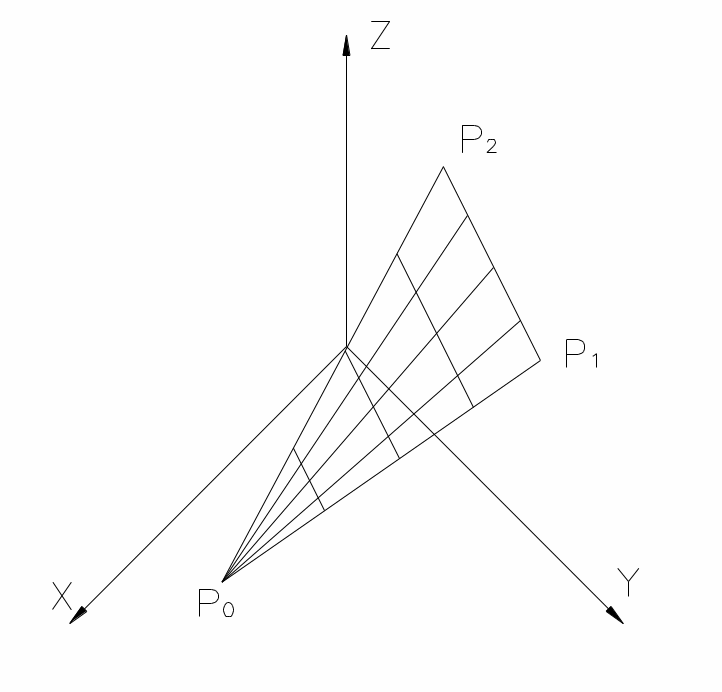 Система
описывает координаты (x,y,z)
точек на плоском треугольнике с вершинами
в точках P0=(3,2,1);
P1=(5,7,6);
P2=(9,10,11)
(Рис. 1.7). Для того, чтобы исклю-чить
точки, лежащие за пределами треугольника
P0P1P2,
дополнительно указана область изменения
независимых параметров u
и v.
Система
описывает координаты (x,y,z)
точек на плоском треугольнике с вершинами
в точках P0=(3,2,1);
P1=(5,7,6);
P2=(9,10,11)
(Рис. 1.7). Для того, чтобы исклю-чить
точки, лежащие за пределами треугольника
P0P1P2,
дополнительно указана область изменения
независимых параметров u
и v.
Рис. 1.7
1.6. Виды поверхностей
1. Цилиндрические поверхности. Образованы прямы-ми, параллельными некоторой оси. Путем поворота и сдви-га системы координат уравнение цилиндрической поверх-ности всегда можно представить в таком виде, когда одна из координат (вдоль оси цилиндра) отсутствует. Например, если ось цилиндра параллельна оси z, то уравнение поверх-ности примет вид:
f(x,y)=0. (1. 12)
К ривая f(x, y)=0 , которая лежит в плоскости z = 0, называется направляющей цилиндрической поверхности.
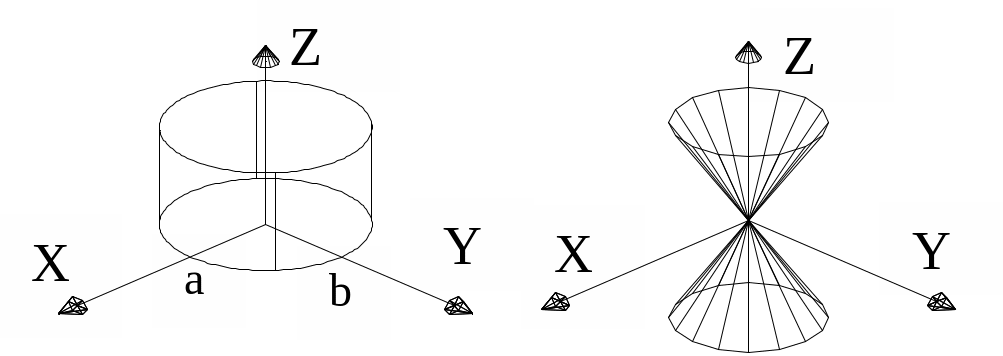 Рис.
1.8 Рис.1.9
Рис.
1.8 Рис.1.9
П![]() ример
1. Уравнение кривой имеет вид:
ример
1. Уравнение кривой имеет вид:
![]()
В 3-мерном пространстве поверхность является цилиндром с направляющим эллипсом в плоскости z = 0 и осью, параллельной оси z (Рис.1.8).
2.Конические поверхности. Образованы прямыми проходящими через некоторую точку (x0,y0,z0), которую на-зывают вершиной конуса. Функция f(x,y,z) обладает следу-ющим свойством:
f(k(x-x0 ), k(y -y0 ),k(z-z0))=kn f(x-x0 ,y-y0 ,z-z0 ). (1.13)
Число n называется степенью конической поверхнос-ти.
