
- •Введение
- •I. Основные виды геометрических объектов в машинной графике
- •1.1. Основные аналитические способы задания кривых
- •3. Параметрический способ задания. В качестве независимой переменной выбирается некоторый параметр t. Все координаты точек на кривой выражаются через него:
- •1.2. Виды кривых
- •1.3. Основные способы задания прямых
- •1.4. Способы задания окружностей и их дуг
- •Углы 0 , 1 находим, как и в п. 2 , по формулам (1.8 б, в).
- •1.5. Основные аналитические способы задания поверхностей
- •1.6. Виды поверхностей
- •П ример 2 .Уравнение конуса второй степени
- •1.7. Основные способы задания плоскостей
- •1.8. Аналитические способы задания пространственных тел
- •1.9. Основные операции с графическими примитивами
- •Как и в п.1, представим условие пересечения в виде
- •1.10. Параметрические кривые и их построение в векторном виде
1.2. Виды кривых
1. Кривые, представимые в алгебраическом виде.
Кривая называется алгебраической степени n, если она может быть представлена в виде (1.2), где f(x, y, z) и g(x, y, z) – многочлены с максимальной степенью n. Наиболее употребительны кривые 1-й и 2-й степени.
а![]() )
Кривые при n
= 1 – прямые
образованы пересечением двух плоскостей:
)
Кривые при n
= 1 – прямые
образованы пересечением двух плоскостей:
б![]() )
Кривые второго порядка (
n
= 2 ) – конические
сечения – могут быть представлены как
различные сечения конуса с круговой
образующей.
)
Кривые второго порядка (
n
= 2 ) – конические
сечения – могут быть представлены как
различные сечения конуса с круговой
образующей.
2.Трансцедентные кривые.
Кривые, не представимые в алгебраическом виде.
1.3. Основные способы задания прямых
Прямые и их части (отрезки, лучи) являются алгебраическими кривыми первого порядка.
1. Канонический способ. С помощью системы уравнений (1.4) как пересечение плоскостей.
2. С помощью направляющего вектора. Уравнение прямой, проходящей через точку (x0,y0,z0), параллельно направля-ющему вектору v=(a, b, c) имеет вид:
3![]() .
Параметрическое задание отрезка, луча
и прямой, проходящих через две точки.
.
Параметрическое задание отрезка, луча
и прямой, проходящих через две точки.
Отрезок прямой, соединяющий точки Р1 и Р2 (как на плоскости, так и в пространстве), задается с помощью параметра u следующим образом:
L(u) =Р1 (1-u) +Р2 u =Р1 +(Р2 -Р1) u; 0 u 1.(1.6)
При этом L(0) =Р1 ; L(1) =Р2 .
Единичный векторt, направленный вдоль отрезка Р1Р2, имеет вид:
![]() .
.
В плоском случаеt=(tx,ty), в пространственном - t=(tx,ty,tz).
Единичная нормаль n+ к плоскому отрезку Р1Р2, повернутая на 90° против часовой стрелки:
n+ =(- ty, tx).
Нормальn -, повернутая на 90° по часовой стрелке:
n - =( ty,- tx).
Векторы, нормальные
к пространственному касатель-ному
вектору t
= (tx
, ty
, tz
), лежат в соответствующих нормальных
плоскостях. Если плоскость задана тремя
точками
![]() ,
,
![]() ,
,
![]() ,
то условие ее перпендикулярности сt
может быть представлено
в виде двух равенств:
,
то условие ее перпендикулярности сt
может быть представлено
в виде двух равенств:
(t
, ![]() )=0;
(t
,
)=0;
(t
, ![]() )=0.
)=0.
Луч, выходящий изР1 и проходящий черезР2, зада-ется аналогично отрезку с той разницей, что 0 u . У прямой, проходящей через Р1 ,Р1 область изменения пара-метра следующая: - . u + . Направляющие векторы и нормали определяются так же , как и для отрезка.
1.4. Способы задания окружностей и их дуг
Окружности и их дуги являются наиболее употреби-тельными алгебраическими кривыми второго порядка. В графических системах они обычно являются стандартными графическими примитивами. Рассмотрим основные спосо-бы задания окружностей и их дуг.
1. Параметрический. В этом случае для дуги указыва-ется центр C(x0,y0), радиус r, начальный и конечный углы 0, 1 (Рис.1.1).
Точки на дуге в зависимости от значения параметра определяют по формулам:
![]() ;
; ![]() . (1.7)
. (1.7)
 У
полной окружности 0
.
Обычно данный способ представления
является основным и все другие сводят
к нему.
У
полной окружности 0
.
Обычно данный способ представления
является основным и все другие сводят
к нему.
Рис. 1.1
По центру C, начальной точке TН и углу (Рис.1.2).
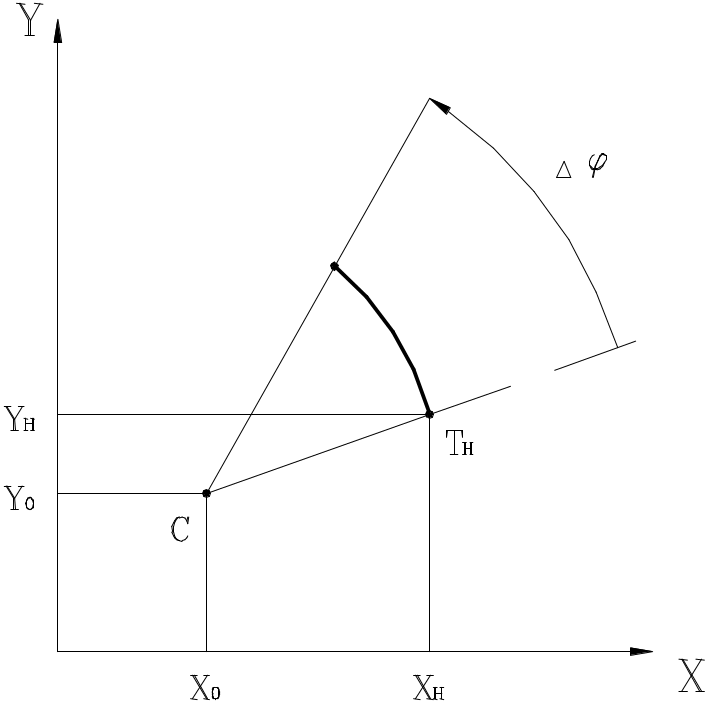 Рис.
1.2
Рис.
1.2
Для перехода к параметрическому заданию рассчита-ем величины r и 0 :
![]() (1.8 а)
(1.8 а)
Если
![]() ,
то
,
то
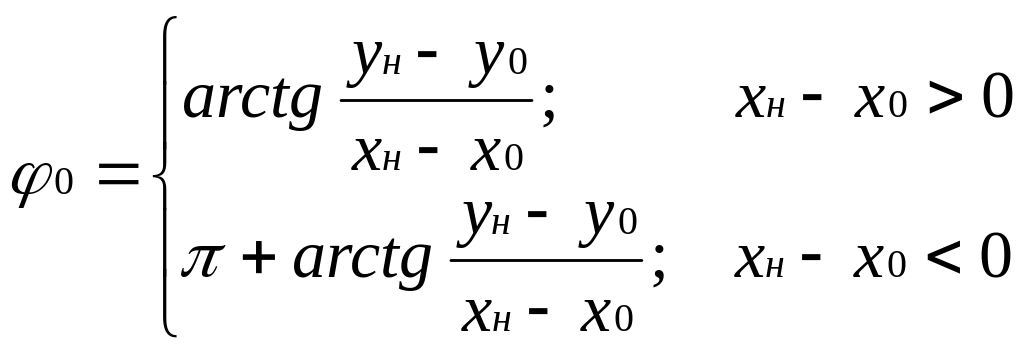 .
(1.8 б)
.
(1.8 б)
Если
![]() ,
то
,
то
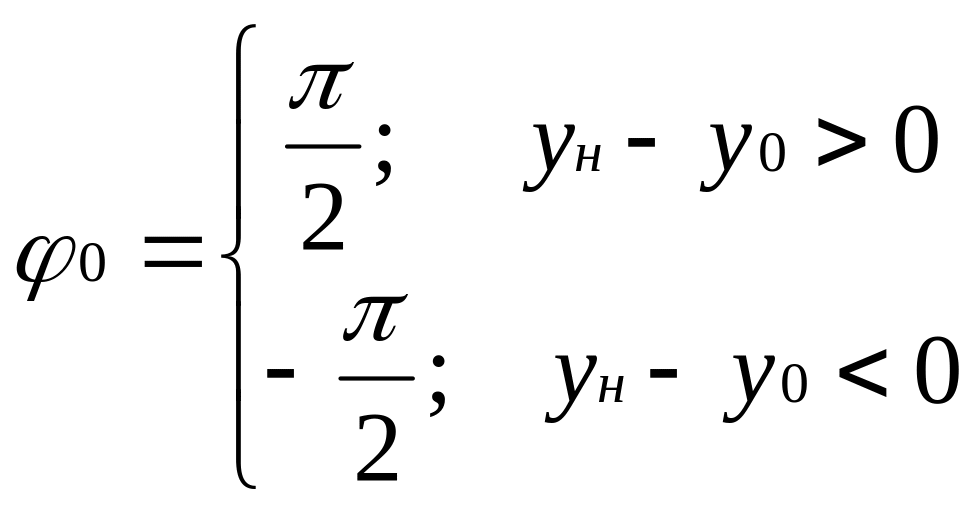 .
(1.8 в)
.
(1.8 в)
Конечный угол 1 =0 + .
3. По начальной T1(x1,y1), средней T2(x2,y2) и конечной T3 (x3,y3) точкам дуги (Рис.1.3).
 Рис.
1.3
Рис.
1.3
Точки не должны лежать на одной прямой. При этом:
![]() .
.
Пусть 0.
Найдем C(x0,y0),
r,
0,
1.
Координаты
![]() центра С определим из системы двух
уравнений:
центра С определим из системы двух
уравнений:
![]() .
.
Введя вспомогательные величины 1 2 = х1 2+ у1 2; 2 2 = х2 2+ у2 2; 3 2 = х3 2+ у3 2; 12 = 1 2 -2 2 , 32 = 3 2 -2 2, можно представить в виде
![]() ,
,![]() .
.
