I. Основные виды геометрических объектов в машинной графике

Любой сложный геометрический объект может быть представлен в виде набора точек, линий, поверхностей и объёмных тел.

Точка является простейшим геометрическим объек-том, не имеющим геометрических размеров. Её можно на-звать объектом нулевой размерности. В любой системе координат положение точки полностью определяется указанием величин всех её координат. Например, в плоской декартовой системе – это значения (x,y), в пространствен-ной – набор величин (x,y,z).

Линия может быть представлена как траектория дви-жения некоторой точки. У неё возникает один геомет-рический размер, называемый длиной (которая может быть как конечной, так и бесконечной). Поэтому линия является одномерным геометрическим объектом (1d-объектом). Спо-соб задания линии зависит, как правило, от способа её порождения и не является единственным.

Поверхность можно представить в виде следа, кото-рый оставляет некоторая линия (в общем случае – перемен-ной формы) при задании ей дополнительного перемещения. Помимо длины у неё появляется второе измерение – ширина. Таким образом, поверхность является двухмерным (2d-объектом).

Телом называется трёхмерный объект (3d-объект), имеющий длину, ширину и высоту.

В геометрических конструкциях, рассматриваемых в САПР, отсутствуют специфические математические аб-страктные объекты (типа ленты Мёбиуса, бутылки Клейна), описание которых требует использования специальных подходов. Поэтому везде в дальнейшем подразумевается, что рассматриваемые объекты не имеют геометрических особенностей.

1.1. Основные аналитические способы задания кривых

1. Явный способ задания. В качестве независимой переменной выбирается, как правило, одна из координат, например, x, а две другие задают в виде функций от x:

y = y(x),

z = z(x), x₀ < x < x₁ . (1.1)

П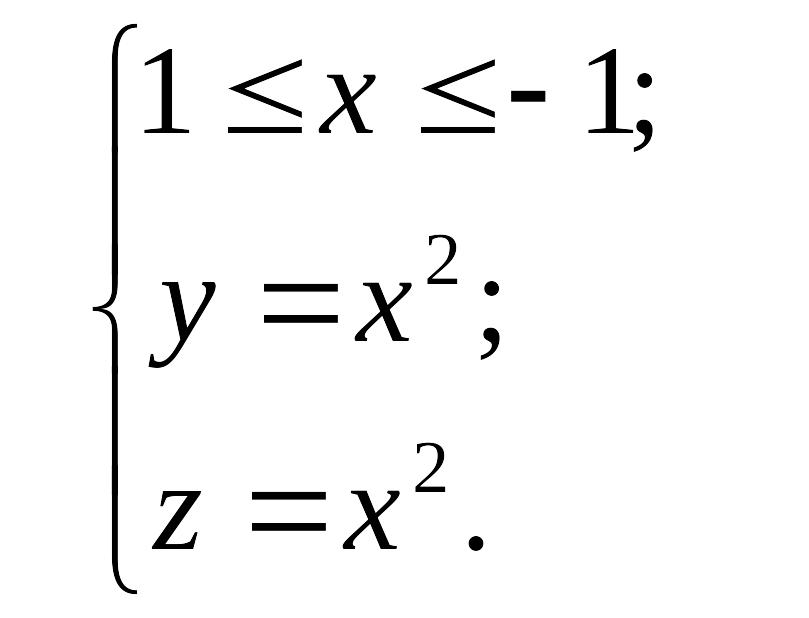 ример 1.

Зависимости задают участок параболы, лежащей в плоскости y = z.

2. Неявный способ задания. Координаты точек задаются системой двух уравнений, описывающих поверх-ности:

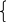f (x,y,z) = 0;

g(x,y,z) = 0. (1.2)

П ример 2.

Приведенная выше система уравнений определяет эл-липс с полуосями (а,b) в плоскости z = 0, который образо-ван пересечением эллипсоида с полуосями (а,b,с) с данной плоскостью.

3. Параметрический способ задания. В качестве независимой переменной выбирается некоторый параметр t. Все координаты точек на кривой выражаются через него:

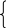x = x(t);

y = y(t); t₀ < t < t₁; (1.3)

z = z(t).

С помощью параметрического задания можно единой формулой описывать многозначные функции, что невоз-можно при явном задании. Параметру t зачастую задаётся некоторый физический смысл, например, времени или угла поворота.

Пример 3.

З ависимости описывают один виток спирали радиуса R с центральной осью z и шагом, равным 2.