Тема 7.

1)

Энергия точечного заряда во внешнем электрическом поле.

Энергия взаимодействия системы точечных неподвижных зарядов.

Энергия взаимодействия двух зарядов: , где - расстояние между зарядами.

Рассмотрим систему из N точечных зарядов. Энергия взаимодействия такой системы = сумме энергий взаимодействия зарядов, взятых попарно: , а . Получаем, . Эту формулу можно преобразовать так: , а , т.е. потенциал, создаваемый всеми зарядами, кроме , в той точке, где помещается заряд . Окончательно получаем, .

2)

Энергия заряженного проводника.

Энергия взаимодействия системы точечных зарядов: , где - потенциал, создаваемый всеми зарядами, кроме , в той точке, где помещается заряд .

Заряд, находящийся на некотором проводнике, можно рассматривать как систему точечных зарядов q. Поверхность проводника является эквипотенциальной, поэтому потенциалы во всех точках одинаковы и равны потенциалу  проводника.

. Используя формулу для емкости проводника, можно получить следующие формулы для энергии: .

Энергия заряженного конденсатора.

Пусть потенциал обкладки конденсатора, заряд на которой +q, = ₁, а с зарядом -q — ₂. Тогда каждый из элементарных зарядов q, на которой можно разделить заряд +q, находится в точке с потенциалом ₁, а каждый из зарядов, на которой можно разделить заряд -q, — в точке с потенциалом ₂.

Энергия такой системы зарядов: .

Используя формулу для емкости конденсатора, можно получить следующие формулы для энергии: .

3)

Энергия электростатического поля.

Энергия заряженного конденсатора через величины, характеризующие электрическое поле в зазоре между обкладками: , - напряженность поля в зазоре между обкладками, - объем, занимаемый полем. Получаем, .

Объемная плотность энергии поля плоского конденсатора: .

В общем случае энергию электрического поля, заключенную в слое между v1 и v2 можно найти по формуле .

Тема 8.

Законы Ома и Джоуля-Ленца. Сопротивление.

1.Сила тока - заряд, протекающий через поперечное сечение проводника в единицу времени I=∂q/∂t. За положительное направление силы тока принимают направление движения положительных зарядов. Плотность тока - вектор, численно равен силе тока ∂I через расположенную в данной точке перпендикулярную к направлению движения носителей площадку ∂S, отнесенной к величине этой площадке j=∂I/∂S. За направление j принимается направление вектора скорости u упорядоченного движения положительных носителей. Зная вектор плотности тока в каждой точке пространства, можно найти силу тока I через любую поверхность S: . N- кол-во зарядов в единице объема V. u-скорость носителей тока u=l/t, n=N/V концентрация. Величина заряда носителей=e. Р-м цилиндр с площадью основания S, образующей l, объема V=Sl. =>

2.Постоянный электрический ток-ток, не изменяющийся во времени.I=q/t. Источник тока - источник электрической энергии, в котором действуют сторонние силы по разделению электрических зарядов. Источник тока характеризуется током и внутренней проводимостью. Источниками тока являются: гальванические элементы, аккумуляторы, машины постоянного тока. Сторонние Силы-силы неэлектрической природы, вызывающие перемещение электрических зарядов внутри источника постоянного тока. Сторонними считаются все силы отличные от кулоновских сил. Возникают в хим. процессах переменного электрического поля. Электродвижущая сила – характеристика источника энергии в электрической цепи. ЭДС измеряется отношением работы сторонних сил по перемещению заряда вдоль контура к величине этого заряда (измеряется в вольтах).E=A/q. ЭДС источника тока- работа по перемещению единичного положительного заряда сторонними силами на участке или по всей длине.

A Кроме сторонних сил на заряд действует силы электростатического поля . Результирующая сила, действующая на заряд равна:

. Работа по перемещению единичного положит. заряда, называется напряжением. . Для однородного участка цепи то есть U совпадает с разностью потенциалов на концах участка.

- закон Ома для неоднородного участка цепи в дифференциальной форме.

, , , -закон Ома для неоднородного участка в интегральной форме. ρ-удельное сопротивление для однородного проводника. - закон Ома для однородного участка

- закон Ома для замкнутой цепи.

3.Электронная теория электропроводности металлов. В металлах носителями тока являются электроны. Теория предполагает, что электроны, подобно молекулам из газа свободно движутся внутри кристаллической решетки металла. В свободном движении принимают участие не все электроны атомов металлов. Электроны, подобно молекулам участвуют в тепловом движении время от времени сталкиваясь с узлами кристаллической решетки, а не с электронами. Средняя скорость теплового движения электрона v= . Помимо теплового электроны участвуют в направленном движении со скоростью u= . λ длина свободного пробега электрона между 2-мя ударами. Применяя 2 закон Ньютона к движению электрона получим ma=F=eE, a= E, u = Et(время между 2-мя столкновениями), t= , u = E, j=enu =en* u .

Закон Ома в дифференциальной форме

∂U=E∂l,σ= ρ-удельная проводимость.j= E=σE.

Затруднения теории. Температурная зависимость сопротивления . Оценка среднего пробега электрона. Теория давала неправильное значение удельной теплоёмкости металла.

4.Закон Джоуля-Ленца. В случае, когда проводник неподвижен и химических превращений в нем не совершается, работа тока идет на увеличение внутренней энергии проводника, в результате чего он нагревается и выделяется тепло Q=UIt=RI t, , . Закон на основе электронной теории электропроводимости металлов. При ударе об узел кристаллической решетки электрон передает ему свою кинетическую энергию . В единице объема n электронов. ,j=σE=>

5.Электрическое сопротивление - основная электрическая хар-ка проводника, величина, характеризующая противодействие электрической цепи или её участка электрическому току. Обусловлено преобразованием эл.энергии в другие виды энергии. Единицей измерения сопротивления служит Ом, равный сопротивлению проводника, в котором при напряжении в 1 В течет ток 1 А. Величина сопротивления зависит от формы и размеров проводника, а также от материала, из которого он изготовлен. Для однородного цилиндрического проводника .  (Ом.м)- удельное сопротивление – это характеристика электрических свойств металла, оно зависит от природы металла и от его температуры. По смыслу  - это электрическое сопротивление единицы длины проводника с единичной площадью поперечного сечения. С увеличением температуры сопротивление металлов увеличивается. При умеренных температурах удельное сопротивление линейно зависит от температуры: зависимость удельного сопротивления металлов от температуры;

Тема9.

1. Сила Лоренца как следствие опытных данных, ее электрическая и магнитная составляющие. Напишите выражение для силы в векторном виде, укажите направления векторов. Дайте определение вектора магнитной индукции

F=Fэ+Fм=qE+q[vB]

(v<<c), B – осн. силовая хар-ка поля.

для v~c.

Сила Лоренца направлена перпендикулярно вектору скорости частицы и перпендикулярно линиям индукции в точке, в которой находится частица. Если она положительно заряжена, то направление силы Лоренца совпадает с направлением векторного произведения вектора индукции и скорости, если частица заряжена отрицательно,то напраление силы противоположно этому векторному произведению.

2. Графическое изображение магнитных полей с помощью линий индукции. Дайте определение линий магнитной индукции. Напишите выражение для индукции магнитного поля прямого длинного проводника с током; изобразите поле с помощью линий индукции.

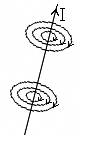
Линии B проводят так, чтобы касатльная к ним в каждой точке совпадала с вектором B в этой точке.

, b – расст. до проводника

3. Напишите выражение для магнитной индукции поля элемента тока (закон Био-Савара-Лапласа) в векторной и скалярной формах, сделайте рисунок, укажите направления векторов. Напишите выражение и дайте формулировку принципа суперпозиции для магнитных полей.

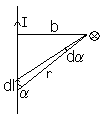
Поле B, порожденное несколькими движущимися зарядами, равно векторной сумме полей, порожденных каждым.

4. Получите с помощью закона Био-Савара-Лапласа и принципа суперпозиции выражение для индукции магнитного поля прямого проводника с током (конечный длины и бесконечно длинного).

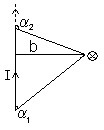
- для конеч. - для бесконеч.

5)

Получите с помощью закона Био-Савара-Лапласа и принципа суперпозиции выражение для индукции магнитного поля на оси и в центре кругового тока.

;

Два диаметрально противоположных элемента образуют равные , но противоположные по направлению.

=>

при h=0 (центр кругового тока)

, тогда магнитный момент контура с током , , при .

6)

Напишите выражение и дайте формулировку теоремы о циркуляции вектора магнитной индукции.

Циркуляция вектора индукции магнитного поля равна произведению магнитной постоянной на сумму токов, которые охватывает контур интегрирования.

Получите с помощью этой теоремы выражение для индукции магнитного поля прямого бесконечно длинного проводника с током.

Рассмотрим плоский контур в виде окружности радиуса b (результат не изменится, если взять произвольный контур с током). В каждой точке этого контура вектор одинаков по величине и направлен по касательной к окружности. => циркуляция = произведению B на длину окружности 2πb. Таким образом, =>

7)

Напишите выражение и дайте формулировку теоремы о циркуляции вектора магнитной индукции.

Циркуляция вектора индукции магнитного поля равна произведению магнитной постоянной на сумму токов, которые охватывает контур интегрирования.

Получите с помощью этой теоремы выражение для индукции магнитного поля внутри длинного соленоида.

Выбираем замкнутый контур-прямоугольник так, чтобы одна из сторон заходила внутрь соленоида а другая нет(эти стороны параллельны оси соленоида, индукция магнитного поля направлена по ней же). Посчитаем циркуляцию вектора индукции по этому замкнутому контуру:

(последний интеграл равен нулю поскольку на участке 3-4 нет магнитной индукции(отсутствует поле))= ( по теореме о циркуляции)= = (n- число витков на единицу длины)

8)

Напишите выражение для потока вектора магнитной индукции через элементарную площадку, поверхность конечных размеров и замкнутую поверхность.

; ( - угол между нормалью к поверхности и направлением индукции магнитного поля)

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Теорема Гаусса для вектора магнитной индукции, напишите выражение и дайте формулировку.

(так как нет магнитных зарядов)

Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю.

Вихревой характер магнитного поля.

, преобразуем левую часть по теореме Стокса: должно быть выполнено для любой поверхности, => . Таким образом, ротор магнитного поля отличен от нуля, такие поля – вихревые.