
- •Механическая система
- •1. Виды механического движения ?
- •Элементарная формула
- •Вид преобразований при коллинеарных осях[4]
- •[Править] Формула преобразования скоростей
- •Классификация сил
- •1. По природе силы:
- •2. По работе, совершаемой силой:
- •Нелинейные деформации
- •[Править] Первый закон Кеплера (закон эллипсов)
- •[Править] Второй закон Кеплера (закон площадей)
- •[Править] Третий закон Кеплера (гармонический закон)
- •Вращающиеся системы отсчета
Элементарная формула
![]()
или
![]()
где
![]() —
нормальное (центростремительное)
ускорение,
—
нормальное (центростремительное)
ускорение,
![]() —
(мгновенная) линейная скорость движения
по траектории,
—
(мгновенная) линейная скорость движения
по траектории,
![]() —
(мгновенная) угловая
скорость этого движения
относительно центра кривизны траектории,
—
(мгновенная) угловая
скорость этого движения
относительно центра кривизны траектории,
![]() —
радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая
—
радиус кривизны траектории в данной
точке. (Cвязь между первой формулой и
второй очевидна, учитывая
![]() ).
).
4.
Прямая задача кинематики. Непрерывность МЛ означает наличие в любой момент времени не только определенного значения координаты частицы, но и ее производной. Исходя из определения производной, имеем: x' = lim x/t = dx/dt. Величина vx = x' называется проекцией мгновенной скорости частицы на ось OX (в нашем случае - просто скоростью частицы) и характеризует направление развития процесса (направление движения вдоль оси OX). В общем случае приращение координаты dx за бесконечно малый промежуток времени dt , а, следовательно, и величина мгновенной скорости зависят от времени (см. рис. 1.7). На графике это проявляется в изменении тангенса угла наклона, образуемого касательной к МЛ и осью Ot. Аналогично вводится понятие мгновенного ускорения: ax = x' = lim x/t = dx/dt. Мгновенное ускорение показывает как быстро изменится скорость при бесконечно малом изменении времени для данного момента t. На практике часто используется понятие средней скорости x ср = x/t. Средняя скорость не является полной характеристикой движения, т.к. ее значение зависит от t. Средняя скорость может быть как положительной, так и отрицательной. В отличии от средней скорости, путь s (расстояние вдоль траектории) и его приращение s за время t могут принимать только положительные значения. Средняя путевая скорость равна: |x ср| = ср = s/t. Понятие среднего ускорения вводится с помощью соотношения: ax ср = x/t.
|
|
|
|
Обратная задача кинематики. Рассмотрим как найти график движения (МЛ) по известной зависимости скорости от времени. Из определения скорости найдем величину конечного перемещения частицы x за промежуток времени t:
Следовательно, положение частицы в любой момент времени задается уравнением:
Значение пути s, пройденного частицей за время t, можно найти, исходя из уравнения:
Используя полученные выражения и определения средней скорости перемещения vx ср и средней путевой скорости vср, найдем выражения для их расчета:
|
|
Враща́тельное движе́ние — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна
При равномерном вращении (T оборотов в секунду),
Частота вращения — число оборотов тела в единицу времени.
![]() ,
,
Период вращения — время одного полного оборота. Период вращения T и его частота ν связаны соотношением T = 1 / ν.
Линейная скорость точки, находящейся на расстоянии R от оси вращения
![]() ,
,
Угловая скорость вращения тела
![]() .
.
Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
![]() ,
,
где: mi — масса i-й точки, ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
Кинетическая энергия вращательного движения
![]()
где Iz — момент инерции тела относительно оси вращения. ω — угловая скорость
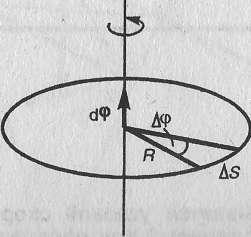
6.Элементарный угол поворота как вектор
Рассмотрим твердое тело, которое вращается вокруг неподвижной оси. Тогда отдельные точки этого тела будут описывать окружности разных радиусов, центры которых лежат на оси вращения. Пусть некоторая точка движется по окружности радиуса R (рис.6). Ее положение через промежуток времени Dt зададим углом Dj. Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Модуль вектора dj равен углу поворота, а его направление совпадает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т. е. подчиняется правилу правого, винта (рис.6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или аксиальными векторами. Эти векторы не имеют определенных точек приложения: они могут откладываться из любой точки оси вращения.
7.
Угловой скоростью
называется векторная величина, равная
первой производной угла поворота тела
по времени:
![]() Вектор
ω
направлен вдоль оси вращения по правилу
правого винта, т. е. так же, как и вектор
dφ
(рис. 2). Размерность угловой скорости
dim ω = Т-1,
а ее единица — радиан в секунду (рад/с).
Вектор
ω
направлен вдоль оси вращения по правилу
правого винта, т. е. так же, как и вектор
dφ
(рис. 2). Размерность угловой скорости
dim ω = Т-1,
а ее единица — радиан в секунду (рад/с).
Линейная
скорость точки (см. рис. 1)
![]()
Угловым
ускорением
называется векторная величина, равная
первой производной yгловой скорости по
времени:
![]()

Рис.3
При вращении тела вокруг неподвижной оси вектор углового ускорения ε направлен вдоль оси вращения в сторону вектора элементарного приращения угловой скорости. При ускоренном движении вектор ε сонаправлен вектору ω (рис. 3), при замедленном - противонаправлен ему (рис. 4).
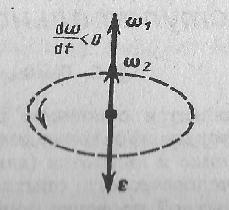
Рис.4
Тангенциальная
составляющая ускорения aτ=dv/dt
, v = ωR и
![]() Нормальная
составляющая ускорения
Нормальная
составляющая ускорения
![]()
8. Связь между линейными и угловыми величинами, характеризующими движение
Отдельные точки вращающегося тела имеют различные линейные скорости v, которые непрерывно изменяют свое направление и зависят от угловой скорости ω и расстояния r соответствующей точки до оси вращения. Точка, находящаяся на расстоянии r от оси вращения проходит путь ΔS = rΔφ. Поделим обе части равенства на
![]() Переходя к пределам
при
Переходя к пределам
при
![]() , получим
, получим
![]() или
или
![]() .
.
Таким
образом, чем дальше отстоит точка от
оси вращения, тем больше ее линейная
скорость. По определению ускорения,
![]() или
или
![]()
![]()
что значения линейной скорости, тангенциального и нормального ускорений растут по мере удаления от оси вращения. Формула устанавливает связь между модулями векторов v, r, ω, которые перпендикулярны друг к другу.

Динамика
1. Фундамента́льные взаимоде́йствия — качественно различающиеся типы взаимодействия элементарных частиц и составленных из них тел.
На сегодня достоверно известно существование четырех фундаментальных взаимодействий:
гравитационного
электромагнитного
сильного
слабого
При этом электромагнитное и слабое взаимодействия являются проявлениями единого электрослабого взаимодействия.
Ведутся поиски других типов фундаментальных взаимодействий, как в явлениях микромира, так и в космических масштабах, однако пока существование какого-либо другого типа фундаментального взаимодействия не обнаружено.
Галилея принцип относительности, принцип физического равноправия инерциальных систем отсчёта в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы. Отсюда следует, что никакими механическими опытами, проводящимися в какой-либо инерциальной системе, нельзя определить, покоится ли данная система или движется равномерно и прямолинейно. Это положение было впервые установлено Г. Галилеем в 1636.
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой справедлив закон инерции: все свободные тела (то есть такие, на которые не действуют внешние силы или действие этих сил компенсируется) движутся прямолинейно и равномерно или покоятся[1]. Эквивалентной является следующая формулировка, удобная для использования в теоретической механике[2]:
Инерциальной называется система отсчёта, по отношению к которой пространство является однородным и изотропным, а время — однородным.
1 закон ньютона- Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальная точка при отсутствии внешних воздействий сохраняет величину и направление своей скорости неограниченно долго.
Преобразова́ния Галиле́я — в классической механике (механике Ньютона) преобразования координат и времени при переходе от одной инерциальной системы отсчета (ИСО) к другой[1]. Преобразования Галилея являются предельным (частным) случаем преобразований Лоренца для скоростей, малых по сравнению со скоростью света в пустоте и в ограниченном объёме пространства. Для скоростей вплоть до порядка скоростей движения планет в Солнечной системе (и даже бо́льших), преобразования Галилея приближенно верны с очень большой точностью.

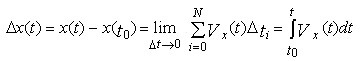 .
(1.1)
.
(1.1)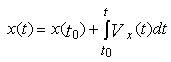 .
(1.2)
.
(1.2)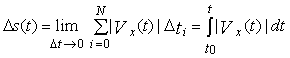 .
(1.3)
.
(1.3)
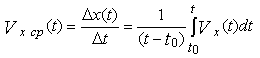 ,
(1.4)
,
(1.4)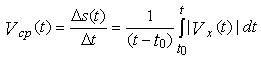 .
(1.5)
.
(1.5)