
- •1.1. Волновое уравнение для электромагнитной волны. Основные свойства электромагнитных волн.
- •1.2. Интенсивность электромагнитной волны. Поведение плоской волны на границе раздела сред.
- •2.1. Световая волна. Показатель преломления среды. Законы геометрической оптики.
- •2.2. Оптическая длина пути. Принцип Ферма. Таутохронность.
- •2.3. Формула тонкой линзы, построение изображений в линзах.
- •Принцип суперпозиции волн. Интенсивность при сложении двух волн.
- •Расчет интерференционной картины от двух источников. Ширина полосы и количество наблюдаемых полос.
- •3.3. Способы получения когерентных источников в оптике: бизеркала Френеля, зеркало Ллойда, бипризма Френеля, билинзаБийе.
- •3.5. Интерференция в тонких пленках. Полосы равной толщины и равного наклона. Кольца Ньютона.
- •4.1. Дифракция света. Дифракция Френеля и дифракция Фраунгофера.
- •Принцип Гюйгенса-Френеля. Зоны Френеля.
- •Дифракция Френеля на круглом отверстии и диске.
- •Дифракция Фраунгофера на длинной щели и двух щелях.
- •4.5. Дифракционная решетка
- •5.1 Естественный и поляризованный свет. Типы поляризации. Степень поляризации.
- •5.2Поляризаторы и анализаторы. Прохождение света через совершенные и несовершенные поляризаторы. Закон Малюса.
- •5.3. Поляризация света при отражении. Закон Брюстера.
- •5.4.Прохождение света через анизотропную среду. Одноосные кристаллы. Обыкновенная и необыкновенная волны.
- •Интерференция поляризованных волн.
- •Искусственная анизотропия. Эффект Керра. Вращение плоскости поляризации (оптическая
- •6.1. Поглощение света. Рассеяние света. Дисперсия света
- •6.2. Тепловое излучение, его характеристики и законы.
- •6.3. Квантовая гипотеза Планка, формула Планка.
- •7.5. Неприменимость понятия траектории к микрочастицам. Соотношение неопределенностей Гейзенберга.
- •7.6. Задание состояния частицы в квантовой механике. Волновая функция и ее статистический смысл. Нормировка.
- •7.7.Стационарные состояния. Временное и стационарное уравнение Шредингера.
- •7.8.Частица в одномерной бесконечно глубокой потенциальной яме. Волновые функции и квантование энергии.
- •7.9.Гармонический осциллятор в квантовой механике.
- •7.10. Прохождение частицы через одномерный потенциальный барьер. Туннельный эффект.
- •7.11.Теория Бора для атома водорода. Экспериментальное подтверждение постулатов Бора. Опыт Франка и Герца.
- •7.12. Квантовомеханическая модель атома водорода. Квантовые числа. Энергия, момент импульса и его проекция для электрона в атоме водорода. Спектральные серии атома водорода.
- •7.13. Пространственное квантование. Опыт Штерна-Герлаха. Спин электрона.
- •7.14. Принцип запрета Паули. Периодическая система элементов. Распределение электронов по оболочкам и подоболочкам в атоме.
7.10. Прохождение частицы через одномерный потенциальный барьер. Туннельный эффект.
Если поместить частицу в потенциальную «яму» с конечной высотой стенок, то с точки зрения законов классической физики она может выйти из этой «ямы» лишь при условии, что ее полная энергия превышает глубину потенциальной «ямы». Иначе, частица, находящаяся внутри потенциальной «ямы», «заперта» в ней.
В
квантовой механике существует
принципиальная возможность прохождения
(«просачивания») частиц сквозь
потенциальные барьеры. Это явление
называется туннельным
эффектом.
Туннельный
эффект возможен, когда линейные размеры
потенциального барьера соизмеримы с
атомными размерами. Для его описания
вводится понятие коэффициента
прозрачности (пропускания)
D потенциального
барьера:
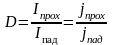 ,
где
,
где
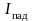 и
и
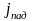 – соответственно
интенсивность волны де Бройля, падающей
на барьер, и плотность потока частиц,
падающих на барьер;
– соответственно
интенсивность волны де Бройля, падающей
на барьер, и плотность потока частиц,
падающих на барьер;
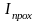 и
и
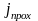 – соответственно
интенсивность де-бройлевской волны,
прошедшей барьер, и плотность потока
частиц, прошедших барьер. Коэффициент
прозрачности D можно рассматривать как
вероятность преодоления частицы
потенциального барьера. Из обратимости
по времени следует, что для переходов
в «прямом» и «обратном» направлениях
коэффициенты прозрачности одинаковы.
– соответственно
интенсивность де-бройлевской волны,
прошедшей барьер, и плотность потока
частиц, прошедших барьер. Коэффициент
прозрачности D можно рассматривать как
вероятность преодоления частицы
потенциального барьера. Из обратимости
по времени следует, что для переходов
в «прямом» и «обратном» направлениях
коэффициенты прозрачности одинаковы.
Аналогично
можно определить коэффициент
отражения барьера
R как
вероятность того, что поток частиц
(частица) отразится от барьера:
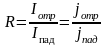 ,
где
,
где
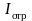 и
и
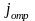 – соответственно
интенсивность волны де Бройля, отразившейся
от барьера, и плотность потока частиц,
отразившихся от барьера и полетевших
в обратном направлении. Расчеты
показывают, что прозрачность барьера
зависит от его «формы» и высоты.
– соответственно
интенсивность волны де Бройля, отразившейся
от барьера, и плотность потока частиц,
отразившихся от барьера и полетевших
в обратном направлении. Расчеты
показывают, что прозрачность барьера
зависит от его «формы» и высоты.
Таким образом, согласно определению, R + D =1. Кроме того, значения R и D не зависят от направления движения частицы.
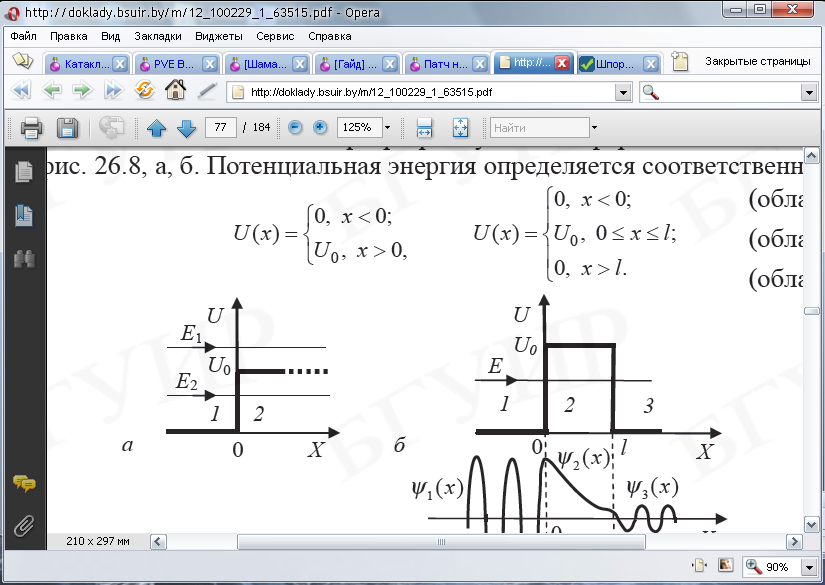
Существуют
два простейших варианта одномерных
потенциальных
барьеров –
прямоугольный потенциальный барьер в
виде ступеньки, когда потенциальная
энергия U при х = 0 скачком изменяется на
конечную величину
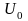 ,
а также
потенциальный барьер прямоугольной
формы высотой
и шириной
,
а также
потенциальный барьер прямоугольной
формы высотой
и шириной
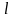 .
Потенциальная энергия определяется
соответственно так:
.
Потенциальная энергия определяется
соответственно так:
а)
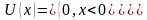 б)
б)
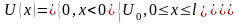
7.11.Теория Бора для атома водорода. Экспериментальное подтверждение постулатов Бора. Опыт Франка и Герца.
Первый постулат Бора (постулат стационарных состояний):
существуют определенные дискретные стационарные состояния атома, находясь в которых, он не излучает энергию. Каждое стационарное состояние характеризуется определенным значением энергии. Из одного состояния в другое атом может переходить путем квантового перехода.
Правило
квантования орбит Бора утверждает,
что в стационарном состоянии атома
электрон, двигаясь по орбите, должен
иметь квантованные значения момента
импульса, удовлетворяющие для круговых
орбит условию
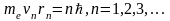 ,
где
,
где
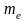 – масса
электрона;
– масса
электрона;
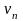 – его скорость
на п-й
орбите радиусом
– его скорость
на п-й
орбите радиусом
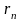 .
.
Второй постулат Бора (правило частот):
излучение
происходит только при переходе атома
из одного стационарного состояния с
большей энергией
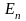 в другое
стационарное состояние с меньшей
энергией
в другое
стационарное состояние с меньшей
энергией
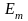 .
Такой переход сопровождается испусканием
электромагнитного излучения с энергией
.
Такой переход сопровождается испусканием
электромагнитного излучения с энергией
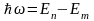 ,
равной разности энергий соответствующих
стационарных состояний. Возможен и
обратный процесс, в котором атом переходит
из одного стационарного состояния в
другое, более высокое. При этом атом
поглощает фотон с энергией, равной
разности энергий этих стационарных
состояний. Набор всевозможных дискретных
частот квантовых переходов ω,
определяемых из правила, описывает
линейчатый
спектр атома.
,
равной разности энергий соответствующих
стационарных состояний. Возможен и
обратный процесс, в котором атом переходит
из одного стационарного состояния в
другое, более высокое. При этом атом
поглощает фотон с энергией, равной
разности энергий этих стационарных
состояний. Набор всевозможных дискретных
частот квантовых переходов ω,
определяемых из правила, описывает
линейчатый
спектр атома.
Дж.
Франк и Г. Герц
(Нобелевская премия, 1925) поставили
эксперимент по измерению потенциалов
ионизации атомов ртути, используя
электродную лампу с четырьмя электродами,
заполненную парами ртути. Исследовалась
зависимость анодного тока I
от ускоряющего
напряжения U.
На анод попадали только те электроны,
энергия которых после соударения с
атомами паров ртути в области
 –
–
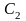 была
достаточна для преодоления замедляющего
напряжения (
была
достаточна для преодоления замедляющего
напряжения (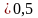 В). Было получено, что величина тока
резко падала при увеличении значения
U через
каждые 4,9 В. Франк и Герц установили, что
спектр поглощаемой атомом ртути энергии
не непрерывен, а дискретен. Минимальная
порция энергии (квант энергии), который
может поглотить атом ртути, равна 4,9 эВ.
Обнаруженное ультрафиолетовое излучение
с длиной волны l
= 253,7 нм
соответствует второму постулату Бора.
Результаты этого опыты впервые доказали
постулаты Бора.
В). Было получено, что величина тока
резко падала при увеличении значения
U через
каждые 4,9 В. Франк и Герц установили, что
спектр поглощаемой атомом ртути энергии
не непрерывен, а дискретен. Минимальная
порция энергии (квант энергии), который
может поглотить атом ртути, равна 4,9 эВ.
Обнаруженное ультрафиолетовое излучение
с длиной волны l
= 253,7 нм
соответствует второму постулату Бора.
Результаты этого опыты впервые доказали
постулаты Бора.
Боровская
модель атома. С
помощью правила квантования для атома
водорода можно получить выражение для
радиуса n-й
стационарной орбиты, по которой движется
электрон – классическая точечная
частица – под действием кулоновской
силы притяжения вокруг ядра:
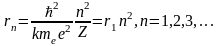 ,
где Z –
количество протонов в ядре;
– масса
электрона;
,
где Z –
количество протонов в ядре;
– масса
электрона;
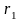 –
радиус первой боровской орбиты (боровский
радиус)
(для атома водорода Z
= 1
и
–
радиус первой боровской орбиты (боровский
радиус)
(для атома водорода Z
= 1
и
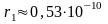 м):
м):
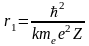 .
.
Э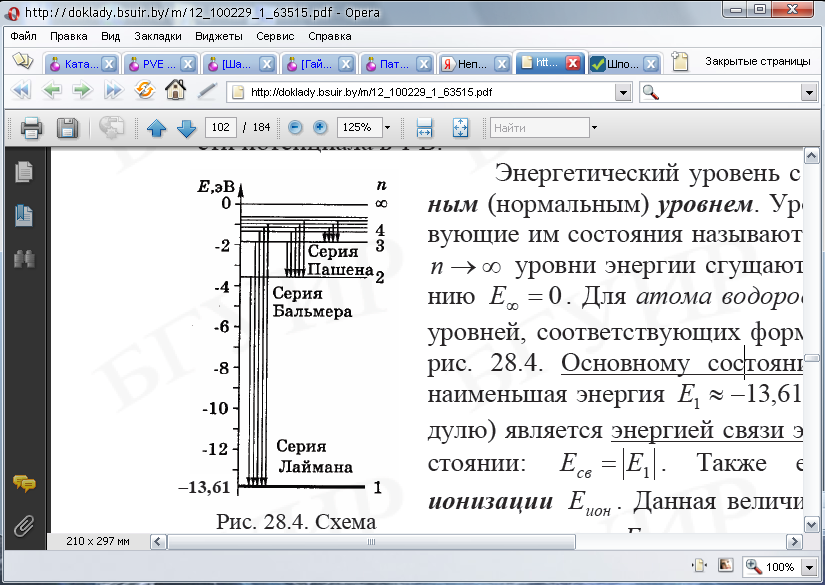 нергия
стационарных
состояний электрона в атоме водорода
и водородоподобной системе на n-й
стационарной орбите ( n
=1, 2, 3, ...)
определяется как полная энергия электрона
в кулоновском поле ядра:
нергия
стационарных
состояний электрона в атоме водорода
и водородоподобной системе на n-й
стационарной орбите ( n
=1, 2, 3, ...)
определяется как полная энергия электрона
в кулоновском поле ядра:
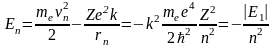 ,
где целое число п
– главное
квантовое число;
,
где целое число п
– главное
квантовое число;
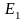 –
энергия основного
состояния
атома (п =
1). Знак минус в формуле означает, что
электрон находится в связанном состоянии.
–
энергия основного
состояния
атома (п =
1). Знак минус в формуле означает, что
электрон находится в связанном состоянии.
