37 Вопрос
Будем считать, что рассматриваемая область односвязная, т.е. в ней нет исключенных участков.
Если замкнутый контур имеет вид, показанный на рисунке, то криволинейный интеграл по контуру L можно записать в виде:
Если участки АВ и CD контура принять за произвольные кривые, то, проведя аналогичные преобразования, получим формулу для контура произвольной формы:
Эта формула называется формулой Остроградского – Грина.
38 Вопрос
Независимость криволинейного интеграла второго рода от пути интегрирования
Условием независимости интегрирования от пути интегрирования будут:
1.
2.
.
3. Существование
потенциала ,
.
Д о к а з а т е л ь с т в о. Пусть есть две точки и их соединяют два пути MAN, MBN (смотри рисунок.).
Пусть выполнено условие 1, тогда
Что и доказывает независимость интеграла от линии интегрирования .
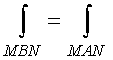
Пусть выполняется условие 2. Из формулы Грина для любой конечной области в этом случае вытекает ,
так как .
Откуда следует условие 1.
Пусть выполняется условие 3. В этом случае выполняется условие 2, а, значит, и 1.
39 Вопрос
Фото
40 Вопрос
Поверхностный интеграл первого рода
Определение
Пусть ф — гладкая,
ограниченная полная поверхность. Пусть
далее на ф задана функция
. Рассмотрим разбиение Т этой поверхности
на части
кусочно-гладкими кривыми и на каждой
такой части выберем произвольную точку
.
Вычислив значение функции в этой точке
и, приняв за
— площадь поверхности
рассмотрим сумму
.
Тогда число
называется пределом сумм
, если:
Предел
сумм
при
называется поверхностным интегралом
первого рода от функции
по поверхности
и обозначается следующим образом:
Параметрическая форма
Пусть на поверхности Ф можно ввести единую параметризацию посредством функций
заданных в ограниченной
замкнутой области
плоскости
и принадлежащих классу
в этой области. Если функция
непрерывна на поверхности Ф , то
поверхностный интеграл первого рода
от этой функции по поверхности Ф
существует и может быть вычислен по
формуле:
, где:
Свойства
Из определения поверхностного интеграла первого рода следует независимость этого интеграла от выбора ориентации векторного поля единичных нормалей к поверхности или, как говорят, от выбора стороны поверхности.
1 Линейность:
;
2 Аддитивность:
;
3 Монотонность:
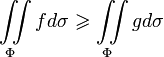
если , то
для
если
, то
4 Теорема о среднем
для непрерывной функции
и замкнутой ограниченной поверхности
:
41 Вопрос
Пример вычисления поверхностного интеграла первого рода
Вычислить поверхностный интеграл
,
где σ — треугольная площадка с вершинами (1, 0, 0); (0, 1, 0) и (0, 0, 1). Направление нормали выбрано таким, что оно образует острый угол с осью Оz (смотри рисунок.).
В соответствии с
выше выведенными формулами, имеем
Из уравнения плоскости x + y + z = 1 находим z = 1 − x − y, и . Подставив эти выражения в интеграл, получим
.