36 Вопрос

Криволинейный интеграл второго рода

Пусть задана некоторая линия γ. Найти работу, которая совершит переменная сила F( x, y ) при перемещении некоторой точки из положения А в положении В по линии γ.

Разобьем линию на бесконечно малые участки точками М1, М2, … , тогда работа силы на всей линии равна сумме работ на каждом участке

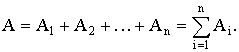
Так как отрезки разбиения бесконечно малы, то их условно можно считать прямолинейными отрезками. Кроме того, будем считать, что в пределах каждой ячейки сила не меняется, и она в пределах ячейки определяется вектором в некоторой точке Ci внутри этой ячейки. Работу внутри каждой ячейки приближенно заменим на элементарную работу силы (скалярное произведение силы на вектор перемещения)

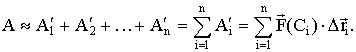
Данная сумма называется криволинейной интегральной суммой второго рода.

Предел криволинейной суммы второго рода, при условии стремления к нулю всех участков разбиения, называется криволинейным интегралом второго рода, если он существует, не зависит от разбиения линии и от выбора точек внутри каждой ячейки

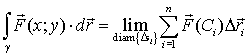
Если вектор силы задан своими координатами, которые являются функциями координат точки

то, воспользовавшись формулой скалярного произведения в координатной форме, получим криволинейный интеграл второго рода в координатной форме:

Свойства криволинейных интегралов второго рода

1 Криволинейный интеграл линейной связки функций равен линейной связки интегралов этих функций

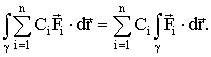
Это свойство означает, что криволинейный интеграл обладает свойством линейности по подынтегральной функции.

2 Если линию интегрирования разбить на части, то интеграл по линии равен сумме интегралов по её частям

Это свойство означает, что криволинейный интеграл обладает свойством аддитивности по линии интегрирования.

3 При изменении направления интегрирования на противоположное направление криволинейный интеграл меняет своё значение на противоположное:

Криволинейный интеграл зависит от направления интегрирования. Следует отметить, что этим свойством не обладает криволинейный интеграл первого рода.

Криволинейный интеграл по замкнутой линии обозначается так

Этот интеграл называется циркуляцией.

Вычисление криволинейного интеграла второго рода, когда линия интегрирования задана в декартовой системе координат

Пусть линия интегрирования задана уравнением у = f (x), тогда криволинейный интеграл от точки А( а, f (а)) до точки В(b, f (b)) приводится к вычислению определённого интеграла

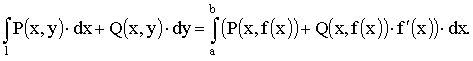
Вычисление криволинейного интеграла второго рода, когда линия интегрирования задана в параметрической форме

Пусть линия интегрирования задана в параметрической форме х = φ(t), у = ψ(t). Тогда

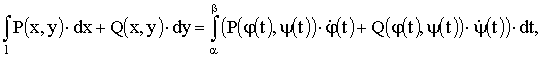
где А( φ(α), ψ(α)), В( φ(β), ψ(β)) и точка сверху означает производную по параметру t.

Пусть l — гладкая, спрямляемая кривая, заданная параметрически (как в определении). Пусть функция определена и интегрируема вдоль кривой l в смысле криволинейного интеграла второго рода. Тогда

,

.

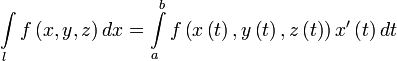
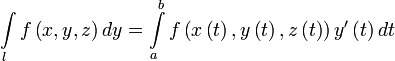
Если обозначить за касательный вектор к кривой l, то нетрудно показать, что