§19 Движения первого и второго рода. Теорема о задании движения, род которого известен.

Теорема 19.1: Если даны точки и , , то существует единственное движение первого рода и существует единственное движение второго рода, в каждом из которых:

, .

Доказательство:

, ,

Если существует , то (18.5)

Таким образом, доказательство существования движения первого рода и его единственности сведется к решению системы (18.5) относительно .

Таким образом, доказательство сводится к доказательству существования единственности решения системы (18.5).

Решение системы (18.5) сводится к решению системы двух линейных уравнений.

(18.6)

.

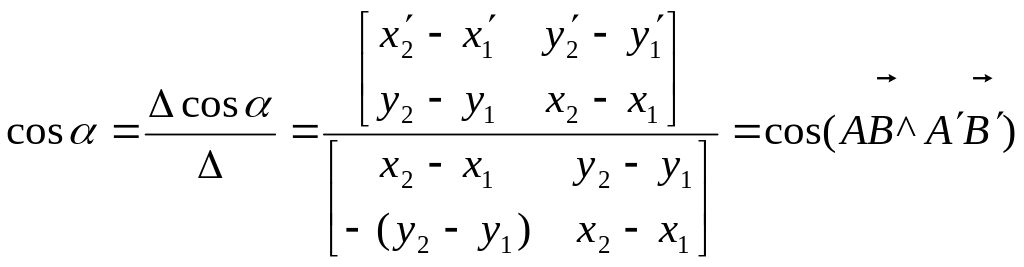
§20 Параллельный перенос.

Определение 20.1: Параллельным переносом (или просто переносом) называется такое преобразование плоскости на себя, при котором , так, что , где - фиксированный вектор, называющийся вектором переноса.

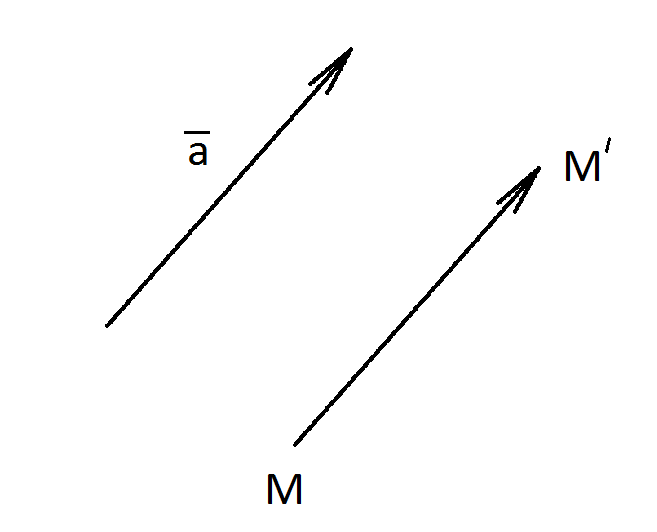
Способы задания :

1) однозначно определяется заданием вектора переноса или парой соответствующих точек и .

2) Координатное задание :

, , , ,   (20.1)

3) Перенос- это движение.

Пусть - произвольные точки плоскости.

. Доказательство проведем методом координат.

, , ,

-движение.

Сравнивая формулы (20.1) и (18.3) делаем вывод, что перенос- движение первого рода.

4) Взаимное расположение соответствующих прямых .

Выясним взаимное расположение и (исследование методом координат).

Пусть задан как в свойстве 3), а , тогда 

Сравнивая уравнения и => т.к. , ,

=> .

 , => .

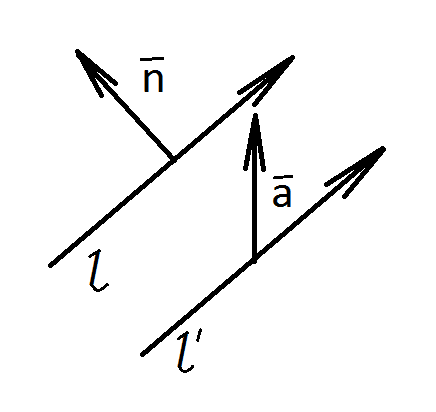
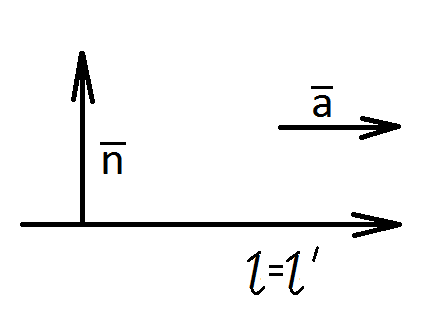
Вывод: в переносе прямая переходит в параллельную ей прямую или в себя.

5) Наличие инвариантных точек ( двойных, неподвижных, переходящих в себя). Исследование вопроса о наличии инвариантных точек сводится к решению системы:

,

Вывод: если , то он не имеет инвариантных точек.

6) Множество - группа.

6.1) , , => =>

=>

6.2) , но т.к. , то =>

Из (6.1) и (6.2) => - группа.

7) Практическое использование :

Из свойств 1-6 следует возможность использования переноса в задачах: на доказательство равенства фигур, на доказательство параллельности прямых, в задачах, в которых рассматриваются параллельные прямые, на построение, сводящихся к построению отрезков заданного направления и заданной длины.

Вывод: Этапы, положенные в основу , определяют общий подход к изучению любого конкретного вида ГПП:

1) конструктивное определение ГПП.

2) выявление способов задания.

3) нахождение координатных формул.

4) выявление, является ли преобразование движением.

5) установление взаимного расположения прямой и ее образа.

6) нахождение инвариантных точек.

7) определение, является ли множество преобразования группой.

8) выявление направлений практического использования ГПП.

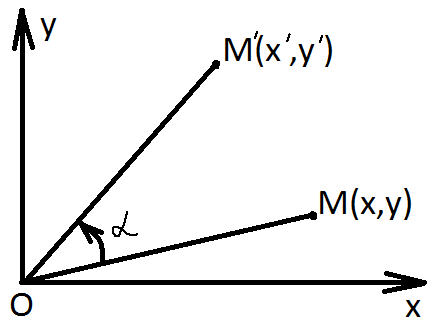
§21 Поворот.

Определение 21.1: Поворотом с центром в точке на угол называется такое ГПП, при котором каждая точка переходит в ( ), что , , .

1) Способы задания.

Из определения 21.1 следует, что определяется центром и углом или центром и точками и .

2) Формулы.

,

(21.1)

3) Выясним, является ли движением:

,

=> - движение.

Сравнивая (21.1) и (18.3) делаем вывод, что - движение первого рода.

4) Взаимное расположение соответствующих прямых.

, т.к.

=> (0,0)- единственное решение.

Вывод: поворот имеет единственную инвариантную точку- центр поворота.

6) - группа.

6.1) =>

=>

6.2) из 6.1=> , , =>

Из 6.1 и 6.2 следует, что - группа.

7) Практическое использование :

Из свойств 1-6 и определения 21.1 следует, что поворот может быть использован в задачах на доказательство равенства фигур; в которых рассматриваются правильные n- угольники; на доказательство того, что треугольник правильный, четырехугольник- квадрат, многоугольник- правильный; в которых рассматривается окружность; на построения, сводящихся к построению равнобедренного треугольника с заданным углом при вершине.