
- •Вопрос 1 Теорема об ограниченности функции, имеющей предел.
- •Вопрос 2 Теорема о переходе к пределу в неравенстве.
- •Вопрос 3 Теорема о пределе промежуточной функции.
- •Вопрос 4 Теорема, устанавливающая связь между функцией, ее пределом и б-м.
- •Вопрос 15 Теорема об ограниченности непрерывной функции.
- •Вопрос 16 Теорема Больцано-Коши (о нуле непрерывной функции)
- •Вопрос 17 Теорема о промежуточном значении непрерывной функции.
- •Вопрос 20 Производные элементарных функций.
- •Вопрос 22 Производные высших порядков, формула Лейбница.
- •Вопрос 24 Теорема Ролля.
- •Вопрос 25 Теорема Кофы.
- •Вопрос 26 Теорема Лагранжа.
- •Вопрос 33 Асимптоты графика. Правило Лопиталя. Интегральное исчисление.
- •Вопрос 37 Интегрирование рациональных дробей.
- •Вопрос 38 Интегрирование иррациональных выражений.
- •Вопрос 39 Интегрирование тригонометрических выражений.
- •Вопрос 40 Понятие интегральной суммы и определенного интеграла. Теоремы об интегрируемой функции.
- •Вопрос 41 Основные свойства определенного интеграла.
- •Вопрос 42 Оценка определенных интегралов.
- •Вопрос 43 Теорема о среднем для определенного интеграла.
- •Вопрос 44 Теорема о производной интеграла с переменным верхним пределом.
- •Вопрос 45 Формула Ньютона-Лейбница.
- •Вопрос 46 Теорема о замене переменной в определенном интеграле.
- •Вопрос 47 Формула интегрирования по частям в определенном интеграле.
- •Вопрос 48 Применение определенного интеграла к вычислению площадей, длин дуг, объемов тел.
- •Вопрос 49
- •Вопрос 50 Вычисление определителей и их свойства.
- •Вопрос 51 Теорема о существовании обратной матрицы.
- •Вопрос 52 Системы линейных уравнений. Решение методом обратной матрицы.
- •Вопрос 53 Теорема Кронеккера-Капелли.
- •Вопрос 54 Метод Гаусса и формулы Крамера.
- •Вопрос 55 Векторы и операции над ними. Их простейшие свойства. Линейная комбинация
- •Вопрос 58
- •59. Векторное произведение двух векторов.
- •Вопрос 60 Смешанное произведение трех векторов
- •Вопрос 61 Уравнение линии на плоскости. Полярная система координат.
- •Вопрос 62 Уравнение поверхности и уравнение линии в пространстве.
- •Уравнение линии в пространстве
- •Вопрос 63 Уравнения прямой на плоскости: общее, каноническое, параметрическое, в отрезках и с угловым коэффициентом.
- •64. Кривые второго порядка.
- •Вопрос 68 Уравнение прямой в пространстве.
- •Вопрос 69 Цилиндрические поверхности. Цилиндрические поверхности
- •Вопрос 70 Поверхности вращения. Поверхности вращения
- •71. Конические поверхности
Вопрос 47 Формула интегрирования по частям в определенном интеграле.
Если
u(x),
v(x)
- непрерывно дифференцируемые функции,
то
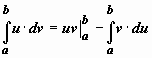 .
Док-во.
Интегрируем равенство
.
Док-во.
Интегрируем равенство
![]() в
пределах от a
до b:
в
пределах от a
до b:
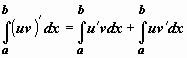 .
Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница
.
Функция в левом интеграле имеет
первообразную uv,
по формуле Ньютона-Лейбница
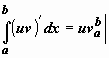 ,
следовательно,
,
следовательно,
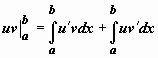 ,
откуда и следует доказываемое равенство.
Пример:
,
откуда и следует доказываемое равенство.
Пример:
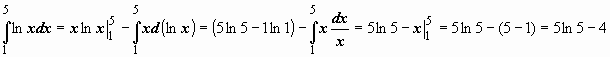 .
.
Вопрос 48 Применение определенного интеграла к вычислению площадей, длин дуг, объемов тел.
Вычисление
площади криволинейной трапеции.
Пусть на отрезке [a,b]
(b>a)
задана непрерывная функция y
= f(x)
, принимающая на этом отрезке неотрицательные
значения :
![]() при
.
Требуется определить площадь S
криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).
при
.
Требуется определить площадь S
криволинейной трапеции ABCD,
ограниченной снизу отрезком [a,b],
слева и справа - прямыми x
= a
и x
= b,
сверху – функцией y
= f(x).
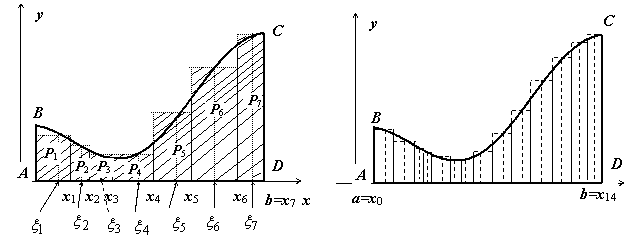 Для
решения этой задачи разделим произвольным
образом основание AD
фигуры точками x0
=
a,
x1
,
x2
,
…, xn-1
=
a,
xn
=
b
на n
частей [x0
,
x1],
[x1
,
x2],
…, [xi-1
,
xi],
…, [xn-1
,
xn];
символом
будем
обозначать длину i-го
отрезка:
.
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
,
найдём
Для
решения этой задачи разделим произвольным
образом основание AD
фигуры точками x0
=
a,
x1
,
x2
,
…, xn-1
=
a,
xn
=
b
на n
частей [x0
,
x1],
[x1
,
x2],
…, [xi-1
,
xi],
…, [xn-1
,
xn];
символом
будем
обозначать длину i-го
отрезка:
.
На каждом из отрезков [xi-1
,
xi]
выберем произвольную точку
,
найдём
![]() ,
вычислим произведение
,
вычислим произведение
![]() (это
произведение равно площади прямоугольника
Pi
с основанием [xi-1
,
xi]
и высотой
)
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначим S
ступ:
(это
произведение равно площади прямоугольника
Pi
с основанием [xi-1
,
xi]
и высотой
)
и просуммируем эти произведения по всем
прямоугольникам. Полученную сумму
обозначим S
ступ:
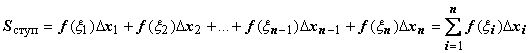 .
Sступ
равно площади ступенчатой фигуры,
образованной прямоугольниками Pi
, i
= 1,2,…,n;
на левом рисунке эта площадь заштрихована.
Sступ
не равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n
отрезков таким образом, чтобы максимальная
длина этих отрезков
.
Sступ
равно площади ступенчатой фигуры,
образованной прямоугольниками Pi
, i
= 1,2,…,n;
на левом рисунке эта площадь заштрихована.
Sступ
не равна искомой площади S,
она только даёт некоторое приближение
к S.
Для того, чтобы улучшить это приближение,
будем увеличивать количество n
отрезков таким образом, чтобы максимальная
длина этих отрезков
![]() стремилась
к нулю (на рисунке ступенчатые фигуры
изображены при n
= 7 (слева) и при n
= 14 (справа)). При
стремилась
к нулю (на рисунке ступенчатые фигуры
изображены при n
= 7 (слева) и при n
= 14 (справа)). При
![]() разница
между Sступ
и S
будет тоже стремиться к нулю, т.е.
разница
между Sступ
и S
будет тоже стремиться к нулю, т.е.
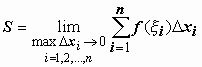 .
.
Вопрос 49
Матрицы. Сложение и умножение матриц, умножение на число.
Матрицей называется таблица чисел вида
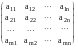
Над матрицами, как и над числами, можно совершать следующие операции, вводимые по определению.
Транспонирование матриц.
АТ называется транспонированной по отношению к матрице Аmxn с элементами aij, если столбцы матрицы АТ являются строками матрицы А, а строки АТ - столбцами матрицы А. Т.е. если Аmxn = (aij), то АТmхn = (aji), i=1,..m, j=1,..n.
 ,
то
,
то
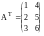
Сложение матриц.
Суммой двух матриц Amxn, Bmxn - одного размера называется матрица Сmxn, того же размера, элементы которой находятся по формуле: сij = aij + bij (i=1, ... m; j= 1, ... n),как суммы соответствующих элементов матриц А и B, при этом пишут:
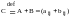 Пример.
Пример.


Умножение матрицы на число.
Произведением матрицы Аmxn на число k называется матрица Сmxn, элементы cij которой находятся по формуле cij = kaij при этом пишут Сmxn = kAmxn
Пример.
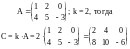
Противоположная матрица.
Противоположной к матрице Аmxn называется матрица, обозначаемая (-А), такая что
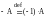
Очевидно что: а) А + (-А) = 0 (сумма матрицы и противоположной к ней есть нулевая матрица)
б) А - В = А + (-В) (разность матриц А и В – это сумма А и противоположной к В матриц)
Умножение матрицы на матрицу.
Произведением матрицы Amxn на матрицу Вnxk называется матрица Сmxk элементы которой находятся по формуле:
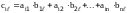 ,
i=1,...m;
=1,2,...k.
,
i=1,...m;
=1,2,...k.
а) А + (-А) = 0 (сумма матрицы и противоположной к ней есть нулевая матрица)
б) А - В = А + (-В) (разность матриц А и В – это сумма А и противоположной к В матриц)
Умножение матрицы на матрицу.
Произведением матрицы Amxn на матрицу Вnxk называется матрица Сmxk элементы которой находятся по формуле:
, i=1,...m; =1,2,...k.
При
этом пишут :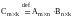
Замечание:
Эта операция существует, если число столбцов матрицы А равно числу строк матрицы В
Пример.
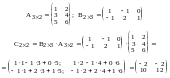
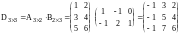
Замечание :Операция умножения матриц не обладает свойством перестановочности, т.е. АВ ВА
Операции над матрицами, введенные выше, обладают следующими свойствами (при выполнении соглашений, оговоренных в определении операций):
А + В = В + А
А + (В + С) = (А + В) + С
(А + В) = А + В
А(В + С)= АВ + АС
(АТ)Т = А
(А + В)Т = АТ + ВТ
(А + В)С = АС + ВС
(АВ) = (А)В = А(В)
А(ВС) = (АВ)С
АЕ = А, (А квадратная матрица )
(А)Т = АТ
(АВ)Т = ВТАТ
