ПРЕДЕЛЫ

Вопрос 1 Теорема об ограниченности функции, имеющей предел.

Пусть функция y=f(x) определена хотя бы в проколотой окрестности точки х₀.

Определение.

Функция y=f(x) называется ограниченной в т. х₀, если k 0 и  0 такие, что из неравенства 0 х-х₀  f(x) k.

Все множество ограниченных при хх₀ функций называют классом ограниченных функций и обозначают О(1), хх₀ (О- большое от единицы). Справедлива следующая теорема.

Теорема.

Если существует предел f(x) при хх₀,то f(x)-ограничена в т. х₀ (f(x)О(1), хх₀)

Доказательство.

Из по критерию существования предела, что f(x)=A+о(1), xx₀. Тогда, т.к. о(1)0, хх₀, тоо(1)1, значит f=A+о(1)A+1=K

Значит по определению f(x)O(1), xx₀.

Ограниченные функции обладают следующими свойствами:

1. Сумма ограниченных при xx₀ функций, есть функция ограниченная.

2. Произведение ограниченных при xx₀ функций есть функция ограниченная.

3. Если f(x)о(1), xx₀, то f(x)О(1), xx₀, т.е. ограничена.

Определение: число А называется пределом y=f(x) в точке х₀ (или при х → х₀), если для любой последовательности допустимых значений х_n ,сходящейся к х_0, последовательность соответствующих значений функции f(x_n), сводится к числу А.

Вопрос 2 Теорема о переходе к пределу в неравенстве.

Теорема. Если f(x)≤g(x), для всех х из некоторой окрестности точки х₀ кроме, быть может. Самой точки х₀ и функции f(x) и g(x) в точке x₀ имеют конечные пределы А и В, то А≤В.

Число А называют пределом функции y=f(x) в т. x₀ и при этом пишут А=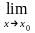 f(x), если для "(любого числа) e >0 (сколь угодно малого) $(найдется число) d_e >0 (зависящее от e) такое, что для "x из неравенства: 0<½x-x₀½<d_eÞ½f(x)-A½<e.

Число А (В,С) называют пределом функции f(x) при х®¥ (х®+¥, х®-¥), и при этом пишут A= (B= ,C= )если для "e >0 $ число N_e>0 такое, что при "½x½>N_e ("x>N_e, "x<-N_e) выполняется неравенство ½f(x)-A½<e (½f(x)-B½<e,

½f(x)-C½<e).

Определение: окрестностью точки А называют любой интервал (a:b), содержащий данную точку. Проколотой окрестностью точки А называется любая точка из окрестности, кроме точки А.

Вопрос 3 Теорема о пределе промежуточной функции.

Теорема. О пределе промежуточной функции.

Если функция f(x)заключена между двумя функциями u(x) и g(x), стремящимися к одному и тому же пределу, то она также стремится к этому пределу, т.е. если

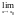u (x)=A и g(x)=A.

u(x)≤f(x)≤g(x), то

f(x)=A.

Вопрос 4 Теорема, устанавливающая связь между функцией, ее пределом и б-м.

Определение: Если a(x) в точке х₀ имеет предел и этот предел равен нулю, то ф-я а(х) называется б-м, при х стремящимся к х₀.

Теорема:Если f(x) определена в некоторой окрестности точки х₀, то для того, чтобы функция f(x) в точке х₀ имела предел А, необходимо и достаточно чтобы f(x) можно было представить в виде суммы a(x)+A, где a(x) – б/м при x→x₀.

Необходимость: если lim f(x) при x→x₀, то f(x)=А+а(х)+б/м x→x₀

Достаточность: Если f(x)=А+а(х), a(x) – б/м при x→x₀, то lim f(x) = A

Вопрос 5

Теорема о сумме двух б-м при х→х₀.

Теорема: сумма(разность) двух бесконечно малых последовательностей есть бесконечно малая последовательность.

Если ф-и а(х) и в(х) – б/м, при х→х_0, то их сумма также б/м

Пример:

Вопрос 6

Теорема о произведении ограниченной величины на б-м.

Теорема: если функция а(х) – б/м при x→x₀, а функция f(x) ограничена в О(х₀), то а(х)*f(x) – б/м при x→x₀

Вопрос 7

Теорема о пределе суммы, произведения, разности, частного функций, имеющих предел.

Теорема: если функции f(x) и g(x) имеют пределы в точке х₀, то в этой точке имеют пределы их сумма, разность, произведение, частное, причем справедливо равенство:

lim (f(x)+g(x)) = lim f(x) + lim g(x) (при x→x₀).

Вопрос 8

Теоремы, устанавливающие связь между б-б и б-м.

Определение. Функция y=f(x) называется бесконечно большой при x®x₀, если для "М>0 (какого угодно большого) найдется число d_М>0 такое, что для "х из неравенства 0<½х-х₀½<d_МÞ½f(x)½>M.

_{При этом пишут}

Вопрос 9

Сравнение б-м. Первый замечательный предел.

Пусть а(х) и b(x) – б-м при x®x₀

Определение1: Если отношение b(x) к а(х) имеет предел в точке х₀ и этот предел равен нулю, то b(x) называют бесконечно малой более высокого порядка, чем а(х).

Определение2: Если отношение b(x) к а(х) имеет предел в точке х₀ и этот предел равен бесконечности, то b(x) называют б/м более низкого порядка, чем а(х).

Определение3: Если отношение b(x) к а(х) имеет предел в точке х₀ и этот предел равен const, то b(x) и а(х) называют б/м одного порядка. А если константа=1, то b(x) и а(х) называют эквивалентными б/м Например, sinX эквивалентно Х, при Х→0

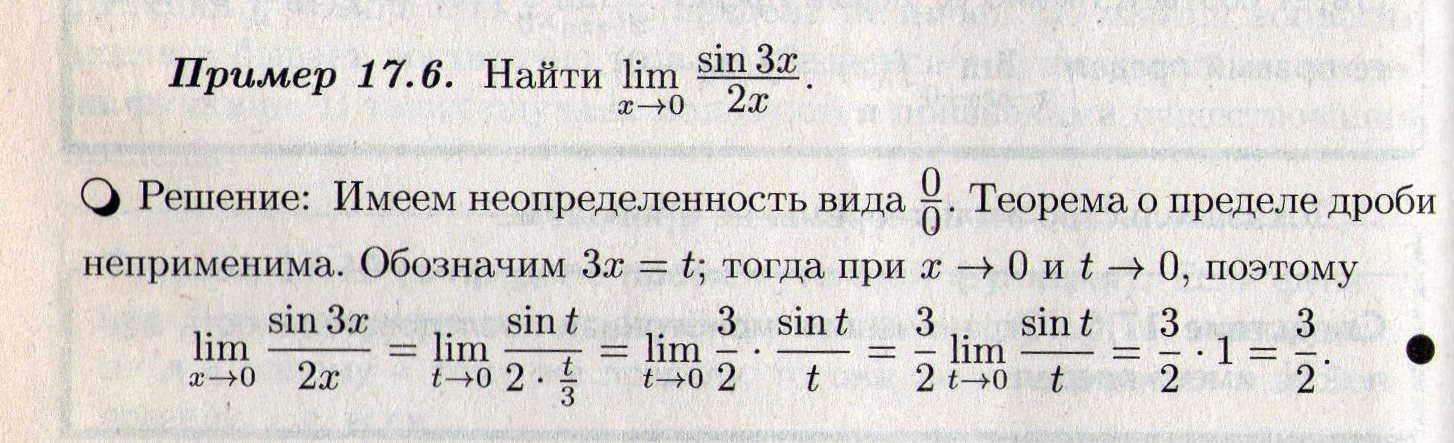
Вопрос 10

Критерий эквивалентности б-м.

Определение: Если отношение b(x) к а(х) имеет предел в точке х₀ и этот предел равен const, то b(x) и а(х) называют б/м одного порядка. А если константа=1, то b(x) и а(х) называют эквивалентными б/м Например, sinX эквивалентно Х, при Х→0.

Вопрос 11

Теорема о замене эквивалентных б-м в пределах.

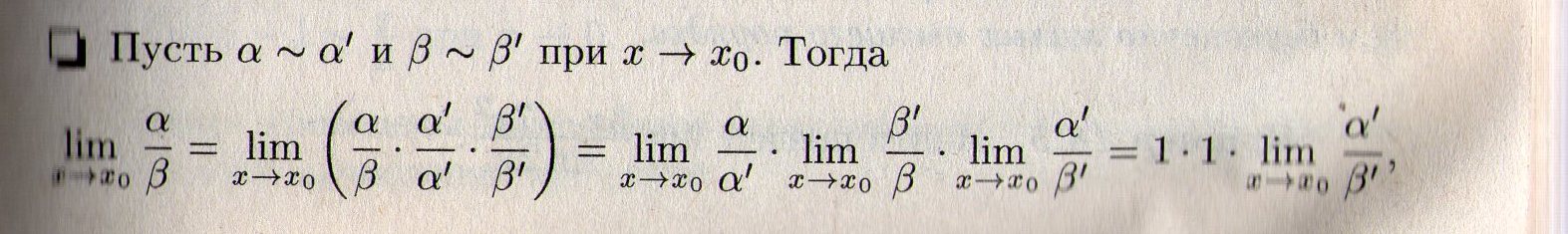
Вопрос 12

Непрерывность суммы, произведения, разности, частного и сложной функций.

Вопрос 13

Точки разрыва и их классификация.

Вопрос 14

Теорема о сохранении знака непрерывной функции.

Теорема. О сохранении знака непрерывной функции.

Если f(x)- непрерывна в т. x₀ и в этой точке f(x₀)>0 (или f(x₀)<0), тогда $U(x₀):"xÎU(x₀) f(x)>0 (или f(x)<0).

Доказательство.

Пусть f(x₀)>0. т.к. f(x)- непрерывна "e>0 $d>0 : для "x из ½x-x₀|<d Þ ½f(x)-f(x₀)½<e. Возьмем e=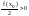 , тогда для этого e $d : "x из ½x-x₀½<d Þ .

Таким образом

$e= , $de>0 : "x Î U(x₀,d) Þ 0<f(x). Здесь U(x₀,d)- окрестность, где функция f(x) сохраняет тот же знак, что и в точке х₀.

Для случая f(x₀)<0 доказательство аналогично .