Вопрос 62 Уравнение поверхности и уравнение линии в пространстве.

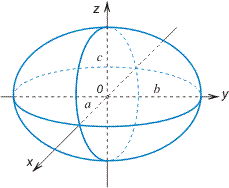
Эллипсоид

a, b, c — полуоси

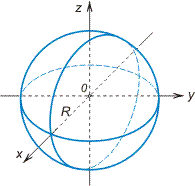
Сфера (частный случай эллипсоида)

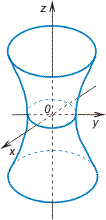
Однополостный гиперболоид

c — действительная полуось, a и b — мнимые полуоси 

Двуполостный гиперболоид

c — действительная полуось, a и b — мнимые полуоси 

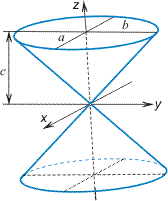
Конус

Вершина конуса в начале координат, направляющая кривая — эллипс с полуосями а и b, плоскость которого находится на расстоянии с от начала координат

 

Эллиптический параболоид

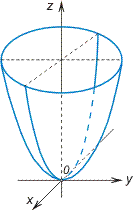
Гиперболический параболоид

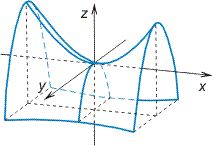
Эллиптический цилиндр

a и b — полуоси

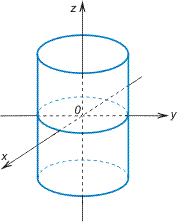
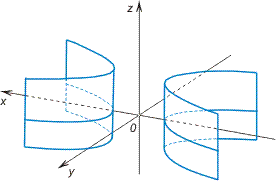Гиперболический цилиндр

Параболический цилиндр

p — фокальный параметр

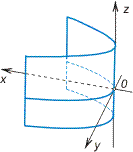
Уравнение линии в пространстве

Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:

F(x, y, z) = 0.

Это уравнение называется уравнением линии в пространстве.

Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана каким- либо уравнением.

Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.

Тогда пару уравнений

назовем уравнением линии в пространстве.

Вопрос 63 Уравнения прямой на плоскости: общее, каноническое, параметрическое, в отрезках и с угловым коэффициентом.

Прямую можно единственным образом задать пересечением двух плоскостей, а значит системой двух уравнений: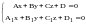

Если прямая проходит через точку ₀(x₀,y₀,z₀) и выбран вектор 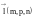- направляющий вектор прямой, то любой вектор на прямой 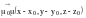коллинеарен вектору .

Если 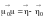, то легко получить векторное уравнение прямой

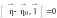
Записав это произведение в координатной форме 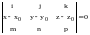, придем к каноническим уравнениям прямой ,

используя тот факт, если определитель равен 0, то его строки пропорциональны.

Приравняв каждую дробь в приведенных выше соотношениях параметру 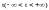, получим параметрические уравнения прямой

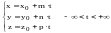
Расстояние от точки ₀ до прямой с направляющим вектором легко найти соединив т. ₀ с любой точкой , лежащей на прямой, и применив формулу

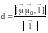
где d - высота параллелограмма, построенного на векторах 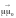и 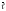. Эта формула в координатной форме имеет вид:

.

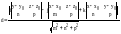64. Кривые второго порядка.

Эллипсом называется г. м. т. плоскости, каждая из которых такова, что сумма расстояний от нее до точек F₁(-c,0) и F₂(c,0) (фокусов) постоянна и равна 2а(c<a,a>0,c>0).

Так как, r₁+r₂=2a, то ,откуда легко, возведением в квадрат, получается каноническое уравнение эллипса

а- большая полуось, b- малая полуось эллипса.

Свойства эллипса.

6. Эллипс целиком лежит в прямоугольнике со сторонами 2а и 2b и центром в начале координат.

7. Эллипс симметричен относительно осей координат.

8. Точки с координатами (а,0), (-а,0), (0,b), (0,-b)- называют вершинами эллипса.

9. В вершинах эллипс касается центров сторон прямоугольника.

10. Число - эксцентриситет, выражающий форму эллипса. При =0 (а=b) - эллипс превращается в окружность.

Определение.

Гипербола- это г. м. т. плоскости модуль разности расстояний от которых до фокусов F₁(-c,0) и F₂(c,0) постоянен и равен 2а.

r₁-r₂=2a или

откуда , после преобразований возведения в квадрат, имеем каноническое уравнение гиперболы.

a,b- полуоси гиперболы.

Свойства гиперболы.

5. Гипербола лежит вне прямоугольника со сторонами 2а и 2b и центром в начале координат.

6. Гипербола симметрична относительно осей координат.

7. Вершины гиперболы- точки А₁(-а,0) и А₂(а,0), в которых она касается середин сторон прямоугольника.

8. При ветви гиперболы стремятся к прямым, являющимся продолжением диагоналей прямоугольника.

Определение.

Парабола- г. м. т. плоскости равноудаленных от точки (фокуса) и прямой, называемой директриссой.

r₁=r₂ или , откуда после преобразований имеем - каноническое уравнение параболы.

Известна следующая теорема, позволяющая классифицировать кривые второго порядка.

Теорема. Любое уравнение кривой второго порядка вида Ax²+2Bxy+Cy²+Dx+Ey+F=0 может быть при помощи поворота декартовой системы координат.

и переноса начала координат , сведено к одному из следующих канонических уравнений

(точка (0,0))

Пример.

Определить тип кривой и построить график 4x²+9y²=16 , это каноническое уравнение эллипса с полуосями a=2, b=4/3

Пример. (Экономическое приложение).

Себестоимость выпуска продукций предприятиями А и В находящихся на расстоянии S друг от друга одинакова. Стоимость перевозки для предприятия А пропорциональна расстоянию с коэффициентом 1/3, для предприятия В с коэффициентом 1. Найти границу рынка сбыта товаров для предприятий А и В.

Граница рынка сбыта будет определяться равенством стоимости продукции, т.е. равенством , где r_A и r_B- расстояние перевозки.

Выражая r_A и r_B имеем

Возводя в квадрат и преобразуя, получаем

.

Это уравнение кривой второго порядка которое приведем к каноническому виду

Получено уравнение окружности (частного случая эллипса) с центром в точке и радиусом . Начертим его, к примеру, при S=8 (R=8)

Из рисунка видно, как накладные расходы, в частности стоимость перевозок, могут сузить рынок сбыта товаров