
- •Вопрос 1 Теорема об ограниченности функции, имеющей предел.
- •Вопрос 2 Теорема о переходе к пределу в неравенстве.
- •Вопрос 3 Теорема о пределе промежуточной функции.
- •Вопрос 4 Теорема, устанавливающая связь между функцией, ее пределом и б-м.
- •Вопрос 15 Теорема об ограниченности непрерывной функции.
- •Вопрос 16 Теорема Больцано-Коши (о нуле непрерывной функции)
- •Вопрос 17 Теорема о промежуточном значении непрерывной функции.
- •Вопрос 20 Производные элементарных функций.
- •Вопрос 22 Производные высших порядков, формула Лейбница.
- •Вопрос 24 Теорема Ролля.
- •Вопрос 25 Теорема Кофы.
- •Вопрос 26 Теорема Лагранжа.
- •Вопрос 33 Асимптоты графика. Правило Лопиталя. Интегральное исчисление.
- •Вопрос 37 Интегрирование рациональных дробей.
- •Вопрос 38 Интегрирование иррациональных выражений.
- •Вопрос 39 Интегрирование тригонометрических выражений.
- •Вопрос 40 Понятие интегральной суммы и определенного интеграла. Теоремы об интегрируемой функции.
- •Вопрос 41 Основные свойства определенного интеграла.
- •Вопрос 42 Оценка определенных интегралов.
- •Вопрос 43 Теорема о среднем для определенного интеграла.
- •Вопрос 44 Теорема о производной интеграла с переменным верхним пределом.
- •Вопрос 45 Формула Ньютона-Лейбница.
- •Вопрос 46 Теорема о замене переменной в определенном интеграле.
- •Вопрос 47 Формула интегрирования по частям в определенном интеграле.
- •Вопрос 48 Применение определенного интеграла к вычислению площадей, длин дуг, объемов тел.
- •Вопрос 49
- •Вопрос 50 Вычисление определителей и их свойства.
- •Вопрос 51 Теорема о существовании обратной матрицы.
- •Вопрос 52 Системы линейных уравнений. Решение методом обратной матрицы.
- •Вопрос 53 Теорема Кронеккера-Капелли.
- •Вопрос 54 Метод Гаусса и формулы Крамера.
- •Вопрос 55 Векторы и операции над ними. Их простейшие свойства. Линейная комбинация
- •Вопрос 58
- •59. Векторное произведение двух векторов.
- •Вопрос 60 Смешанное произведение трех векторов
- •Вопрос 61 Уравнение линии на плоскости. Полярная система координат.
- •Вопрос 62 Уравнение поверхности и уравнение линии в пространстве.
- •Уравнение линии в пространстве
- •Вопрос 63 Уравнения прямой на плоскости: общее, каноническое, параметрическое, в отрезках и с угловым коэффициентом.
- •64. Кривые второго порядка.
- •Вопрос 68 Уравнение прямой в пространстве.
- •Вопрос 69 Цилиндрические поверхности. Цилиндрические поверхности
- •Вопрос 70 Поверхности вращения. Поверхности вращения
- •71. Конические поверхности
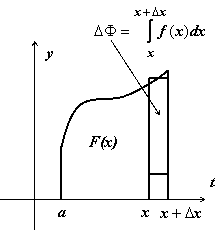
Вопрос 44 Теорема о производной интеграла с переменным верхним пределом.
Интеграл
с переменным верхним пределом. Значение
определённого интеграла не зависит от
того, какой буквой обозначена переменная
интегрирования:
 (чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквой t,
а буквой x
обозначим верхний предел интегрирования.
Будем считать, что верхний предел
интеграла может меняться, т.е. что x
- переменная, в результате интеграл
будет функцией Ф(x)
своего верхнего предела:
(чтобы
убедиться в этом, достаточно выписать
интегральные суммы, они совпадают). В
этом разделе переменную интегрирования
будем обозначать буквой t,
а буквой x
обозначим верхний предел интегрирования.
Будем считать, что верхний предел
интеграла может меняться, т.е. что x
- переменная, в результате интеграл
будет функцией Ф(x)
своего верхнего предела:
 .
Легко доказать, что если f(t)
интегрируема, то Ф(x)
непрерывна, но для нас важнее следующая
фундаментальная теорема:
Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t)
непрерывна в окрестности точки t
= x,
то в этой точке функция Ф(x)
дифференцируема, и
.
Легко доказать, что если f(t)
интегрируема, то Ф(x)
непрерывна, но для нас важнее следующая
фундаментальная теорема:
Теорема
об интеграле с переменным верхним
пределом.
Если функция f(t)
непрерывна в окрестности точки t
= x,
то в этой точке функция Ф(x)
дифференцируема, и
![]() .
Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом пределе.
Док-во.
Дадим верхнему пределу x
приращение
.
Другими
словами, производная определённого
интеграла от непрерывной функции по
верхнему пределу равна значению
подынтегральной функции в этом пределе.
Док-во.
Дадим верхнему пределу x
приращение
![]() .
Тогда
.
Тогда

 ,
где c
- точка, лежащая между x
и
,
где c
- точка, лежащая между x
и
![]() (
( существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
существование
такой точки утверждается теоремой о
среднем; цифры над знаком равенства -
номер применённого свойства определённого
интеграла).
![]() .
Устремим
.
Устремим
![]() .
При этом
.
При этом
![]() (c-
точка, расположенная между x
и
).
Так как f(t)
непрерывна в точке t
= x,
то
(c-
точка, расположенная между x
и
).
Так как f(t)
непрерывна в точке t
= x,
то
![]() .
Следовательно,
существует
.
Следовательно,
существует
![]() ,
и
.
Теорема доказана.
,
и
.
Теорема доказана.
Отметим первое важное следствие этой теоремы. По существу, мы доказали, что любая непрерывная функция f(x) имеет первообразную, и эта первообразная определяется формулой . Другим важным следствием этой теоремы является формула Ньютона-Лейбница, или основная формула интегрального исчисления.
Вопрос 45 Формула Ньютона-Лейбница.
Если
f(x)
непрерывна на отрезке [a,
b],
и F(x)
- некоторая первообразная функции
![]() ,
то
,
то
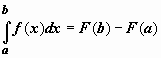 .
Док-во.
Мы установили, что функция
-
первообразная непрерывной f(x).
Так как F(x)
- тоже первообразная, то Ф(x)
= F(x)
+ C.
Положим в этом равенстве x
= a.
Так как
.
Док-во.
Мы установили, что функция
-
первообразная непрерывной f(x).
Так как F(x)
- тоже первообразная, то Ф(x)
= F(x)
+ C.
Положим в этом равенстве x
= a.
Так как
 ,
то
,
то
 .
В равенстве
.
В равенстве
 переобозначим
переменные: для переменной интегрирования
t
вернёмся к обозначению x
, верхний предел x
обозначим b.
Окончательно,
.
Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным символом:
переобозначим
переменные: для переменной интегрирования
t
вернёмся к обозначению x
, верхний предел x
обозначим b.
Окончательно,
.
Разность
в правой части формулы Ньютона-Лейбница
обозначается специальным символом:
![]() (здесь
(здесь
![]() читается
как "подстановка от a
до b"),
поэтому формулу Ньютона-Лейбница обычно
записывают так:
читается
как "подстановка от a
до b"),
поэтому формулу Ньютона-Лейбница обычно
записывают так:
 .
Пример
применения формулы Ньютона-Лейбница:
.
Пример
применения формулы Ньютона-Лейбница:
 .
.
Вопрос 46 Теорема о замене переменной в определенном интеграле.
Теорема.
Пусть функция
![]()
определена, непрерывно дифференцируема и монотонна на отрезке
 ,
,
 ,
,
функция непрерывна на отрезке [a, b].
Тогда
 .
.
Док-во.
Пусть F(x)
- первообразная для функции f(x),
т.е.
![]() ,
тогда
,
тогда
![]() -
первообразная для функции
-
первообразная для функции
![]() .
.
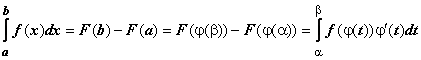 ,
что и требовалось доказать.
,
что и требовалось доказать.
При решении задач нельзя забывать о том, что при переходе к новой переменной надо обязательно вычислить новые пределы интеграла. Пример:

 .
.
