
- •Вопрос 1 Теорема об ограниченности функции, имеющей предел.
- •Вопрос 2 Теорема о переходе к пределу в неравенстве.
- •Вопрос 3 Теорема о пределе промежуточной функции.
- •Вопрос 4 Теорема, устанавливающая связь между функцией, ее пределом и б-м.
- •Вопрос 15 Теорема об ограниченности непрерывной функции.
- •Вопрос 16 Теорема Больцано-Коши (о нуле непрерывной функции)
- •Вопрос 17 Теорема о промежуточном значении непрерывной функции.
- •Вопрос 20 Производные элементарных функций.
- •Вопрос 22 Производные высших порядков, формула Лейбница.
- •Вопрос 24 Теорема Ролля.
- •Вопрос 25 Теорема Кофы.
- •Вопрос 26 Теорема Лагранжа.
- •Вопрос 33 Асимптоты графика. Правило Лопиталя. Интегральное исчисление.
- •Вопрос 37 Интегрирование рациональных дробей.
- •Вопрос 38 Интегрирование иррациональных выражений.
- •Вопрос 39 Интегрирование тригонометрических выражений.
- •Вопрос 40 Понятие интегральной суммы и определенного интеграла. Теоремы об интегрируемой функции.
- •Вопрос 41 Основные свойства определенного интеграла.
- •Вопрос 42 Оценка определенных интегралов.
- •Вопрос 43 Теорема о среднем для определенного интеграла.
- •Вопрос 44 Теорема о производной интеграла с переменным верхним пределом.
- •Вопрос 45 Формула Ньютона-Лейбница.
- •Вопрос 46 Теорема о замене переменной в определенном интеграле.
- •Вопрос 47 Формула интегрирования по частям в определенном интеграле.
- •Вопрос 48 Применение определенного интеграла к вычислению площадей, длин дуг, объемов тел.
- •Вопрос 49
- •Вопрос 50 Вычисление определителей и их свойства.
- •Вопрос 51 Теорема о существовании обратной матрицы.
- •Вопрос 52 Системы линейных уравнений. Решение методом обратной матрицы.
- •Вопрос 53 Теорема Кронеккера-Капелли.
- •Вопрос 54 Метод Гаусса и формулы Крамера.
- •Вопрос 55 Векторы и операции над ними. Их простейшие свойства. Линейная комбинация
- •Вопрос 58
- •59. Векторное произведение двух векторов.
- •Вопрос 60 Смешанное произведение трех векторов
- •Вопрос 61 Уравнение линии на плоскости. Полярная система координат.
- •Вопрос 62 Уравнение поверхности и уравнение линии в пространстве.
- •Уравнение линии в пространстве
- •Вопрос 63 Уравнения прямой на плоскости: общее, каноническое, параметрическое, в отрезках и с угловым коэффициентом.
- •64. Кривые второго порядка.
- •Вопрос 68 Уравнение прямой в пространстве.
- •Вопрос 69 Цилиндрические поверхности. Цилиндрические поверхности
- •Вопрос 70 Поверхности вращения. Поверхности вращения
- •71. Конические поверхности
Вопрос 25 Теорема Кофы.
Д о к а з а т е л ь с т в о. Составим уравнение хорды, проходящей через точки (a, f(a)), (b, f(b))
y = f(a) + Q·(x - a),
где![]() есть угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
есть угловой коэффициент хорды. Рассмотрим
разность ординат функции и хорды
F(x) = f(x) − f(a) − Q·(x − a).
Очевидно,
что функция F(x)
удовлетворяет всем условиям теоремы
Ролля. Поэтому на интервале (a,
b)
найдётся такая точка с, для которой F
' (c)
= 0. То есть F
' (c)
= f
' (c)
− Q
= 0. Откуда следует
![]()
И, наконец, f(b) − f(a) = f '(c)·(b − a).
Вопрос 26 Теорема Лагранжа.
Д о к а з а т е л ь с т в о. Покажем сначала, что знаменатель левой части формулы не обращается в ноль. Если допустить, что g(b) = g(a), то по теореме Ролля для функции g(x) найдется точка x Î (a, b), в которой g ' (x) = 0. А это противоречит условию, что g ' (x) ≠ 0 на (a, b).
Рассмотрим
функцию
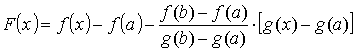
Функция
F(x)
на [a,
b]
удовлетворяет условиям теоремы Ролля:
F(x)
непрерывна на [a,
b],
дифференцируема на (a,
b),
и, кроме того, на концах интервала
принимает равные значения F(a)
= F(b)
= 0. По теореме Ролля для F(x)
существует точка c
Î (a,
b)
, такая ,что F
' (c)
= 0. Так
как
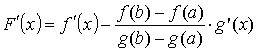 ,
,
То

Откуда, учитывая, что g '(c) ≠ 0, следует искомое соотношение.
Вопрос 33 Асимптоты графика. Правило Лопиталя. Интегральное исчисление.
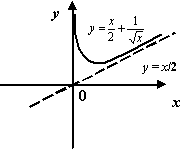
Рассмотрим
функцию
 .
График этой функции имеет наклонную
асимптоту
.
График этой функции имеет наклонную
асимптоту
![]() при
при
![]() .
Действительно,
.
Действительно,
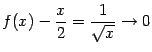
при
![]()
Однако
эта функция не определена ни на каком
луче вида
![]() ,
так что её график не может иметь асимптоты
при
,
так что её график не может иметь асимптоты
при![]()
Вопрос 37 Интегрирование рациональных дробей.
Рациональной
дробью называют выражение вида
 ,
где
,
где
 ,
,
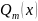 – многочлены степеней n
и m
степеней соответственно. Если
– многочлены степеней n
и m
степеней соответственно. Если
 ,
рациональная дробь называется правильной,
в противном случае
,
рациональная дробь называется правильной,
в противном случае
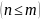 – неправильной.
– неправильной.
Если дробь неправильная, из нее можно выделить целую часть, разделив числитель и знаменатель.
Например,
 – неправильная рациональная дробь.
– неправильная рациональная дробь.
Выполняем деление:
- |
|
|
|
||
- |
|
|
- |
|
|
|
14x+8 - остаток |
|
Таким образом, неправильную дробь можно представить в виде суммы целой рациональной функции (многочлена) и правильной дроби:

Простейшими рациональными дробями называются правильные рациональные дроби следующих четырех типов:
|
|
|
|
Где
A, B, C, a, p, q – числа,
 ,
,

Покажем на примерах, как интегрируются дроби каждого типа.
Дробь 1-го типа:
 .
.
Дробь 2-го типа:
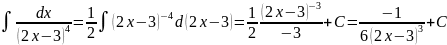 .
.
Постановка задачи. Найти неопределенный интеграл
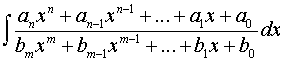 .
.
План решения.
1. Введем обозначения:
![]() ,
,
![]() .
.
Сравним
степени числителя
![]() и
знаменателя
и
знаменателя
![]() .
.
Если
подынтегральная функция – неправильная
рациональная дробь, т.е. степень числителя
![]() больше
или равна степени знаменателя
больше
или равна степени знаменателя
![]() ,
то сначала выделяем целую часть
рациональной функции, поделив числитель
на знаменатель:
,
то сначала выделяем целую часть
рациональной функции, поделив числитель
на знаменатель:
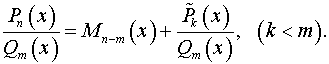
Здесь
многочлен
![]() –
остаток от деления
на
,
причем степень
меньше
степени
.
–
остаток от деления
на
,
причем степень
меньше
степени
.
2. Разложим правильную рациональную дробь
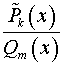
на
элементарные дроби. Если ее знаменатель
имеет простые вещественные корни
![]() ,
т.е.
,
т.е.
![]() ,
то разложение на элементарные дроби
имеет вид
,
то разложение на элементарные дроби
имеет вид
 .
.
3.
Для вычисления неопределенных
коэффициентов
![]() приводим
к общему знаменателю дроби в правой
части равенства, после чего приравниваем
коэффициенты при одинаковых степенях
приводим
к общему знаменателю дроби в правой
части равенства, после чего приравниваем
коэффициенты при одинаковых степенях
![]() в
числителях слева и справа. Получим
систему
уравнений
с
неизвестными,
которая имеет единственное решение.
в
числителях слева и справа. Получим
систему
уравнений
с
неизвестными,
которая имеет единственное решение.
4. Интегрируем целую часть (если она есть) и элементарные дроби, используя табличные интегралы, и записываем ответ
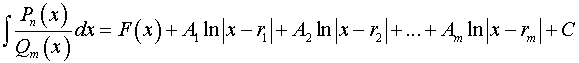 ,
,
где
![]() –
многочлен степени
–
многочлен степени
![]() .
.





 -1
-1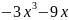

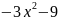
 ,
, ,
, ,
, .
.