Вопрос 54 Метод Гаусса и формулы Крамера.

Теорема

Если для СЛУ АХ = В матрица А невырождена, то решение системы может быть найдено по правилу Крамера

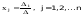
Здесь _j - определитель матрицы, полученной из матрицы А заменой j - столбца столбцом свободных членов.

Пример.

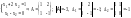
то есть решение

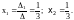
ЗАМЕЧАНИЕ

Для решения СЛУ с матрицей А размера выше 4 метод Крамера не стоит применять, т.к. число операций при применении этого метода имеет порядок n!, т.е. быстро растет с порядком системы. (n!=n(n-1)(n-2)...321, 5!=54321=120).

При решении СЛУ высокого порядка лучше применять метод Гаусса. Суть метода Гаусса состоит в том, что при помощи преобразований, не нарушающих равносильности, исходная система сводится к треугольному виду. Пример.

Решить систему уравнений:

Шаг 1. Делим коэффициенты первого уравнения на коэффициент а₁₁0, при этом получается равносильная система уравнений.

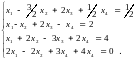
Шаг 2. На месте 2 и 3 уравнений поставим сумму 1-го уравнения, умноженного на (-1), и 2,3- уравнений. На месте 4-го уравнения сумму 1-ой строки, умноженную на (-2), и 4-ой строки. Для краткости записей воспользуемся понятием расширенной матрицы и эквивалентных преобразований

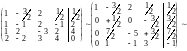
Т. к. во 2, 3, 4 уравнениях неизвестное х₁- исключено, то применим схему приведенную выше для исключения неизвестных в системе, состоящей из 2, 3, 4 уравнений. Для этого вторую строку разделим на 1/2, на месте 3, поставим сумму элементов 2 строки, умноженную на (-7/2), и 3-й строки на месте 4-ой строки сумму элементов 2 строки умноженную на (-1) и 4 строки.

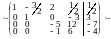
Исключая неизвестные в 3 и 4 уравнениях по той же схеме завершим прямой ход метода Гаусса.

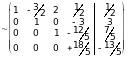
Используя обратный ход метода Гаусса, имеем:

.

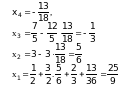Вопрос 55 Векторы и операции над ними. Их простейшие свойства. Линейная комбинация

Вектором называется направленный отрезок, обозначаемый или .

Точка А – начало вектора, точка В – конец.

Если начало и конец вектора совпадают, то говорят что имеется нулевой вектор.

Длинной вектора (модулем) называется число, равное длине отрезка АВ. Это число обозначают   или  . Очевидно что  =0, направление его произвольно.

Векторы, лежащие на одной прямой или на параллельных прямых, называют коллинеарными.

Векторы, лежащие в одной плоскости или на параллельных плоскостях называют компланарными.

Над векторами можно совершать операции, вводимые по определению.

Суммой двух векторов и 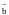называется вектор , начало которого совпадает с началом вектора , а конец совпадает с концом вектора , при этом конец вектора и начало вектора - совмещены (правило треугольника)

Произведением вектора на число k называют вектор =  , имеющий длину  =k  и направление как у вектора , если k > 0, и противоположное направление, если к < 0.

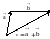
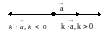
Противоположным к вектору называют вектор

- = (-1) (произведению числа (-1) на вектор ). Разность векторов и – это сумма вектора и -

ЗАМЕЧАНИЕ

Если сумма + – одна диагональ параллелограмма, то разность ( - ) – другая диагональ.

Координатами вектора назовем координаты его конечной точки при условии, что начало совпадает с началом координат.

К примеру в декартовой прямоугольной системе координат имеем

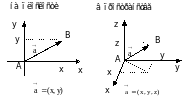
Сумма, разность и произведение вектора на число в координатной форме выглядят так

= + =(x₁+x₂, y₁+y₂, z₁+z₂), 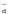= - =(x₁–x₂, y₁–y₂, z₁–z₂), = =(x₁, y₁, z₁), здесь =(x₁, y₁, z₁), =(x₂, y₂, z₂).

В декартовой прямоугольной системе координат очевидно что длина вектора (модуль  ) вычисляется по формулам:

или ,

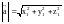как корень квадратный из суммы квадратов координат.