23. Построение мп-преобразователя, реализующего левый разбор

МП-преобразование:

P = <Q,A,Г,В,б,q₀,z₀,F>

Б: Q x (A ∪ { λ}) x Г -> 2QxГ*xB* - множество всех подмножеств.

Спуск по таблице вниз

Раз S ∈ t_1n, B = abaab

S -> AS ? нет

S -> AA ? есть. Используем первое правило, которое нашли.

S - > AA

t₁₁ t₂₄

Эти соответствия ищем просматривая вертикаль вверх, диагональ вниз и до первого нахождения таких t_ij, t_j+1,k. Процесс повторяем параллельно для двух веток.

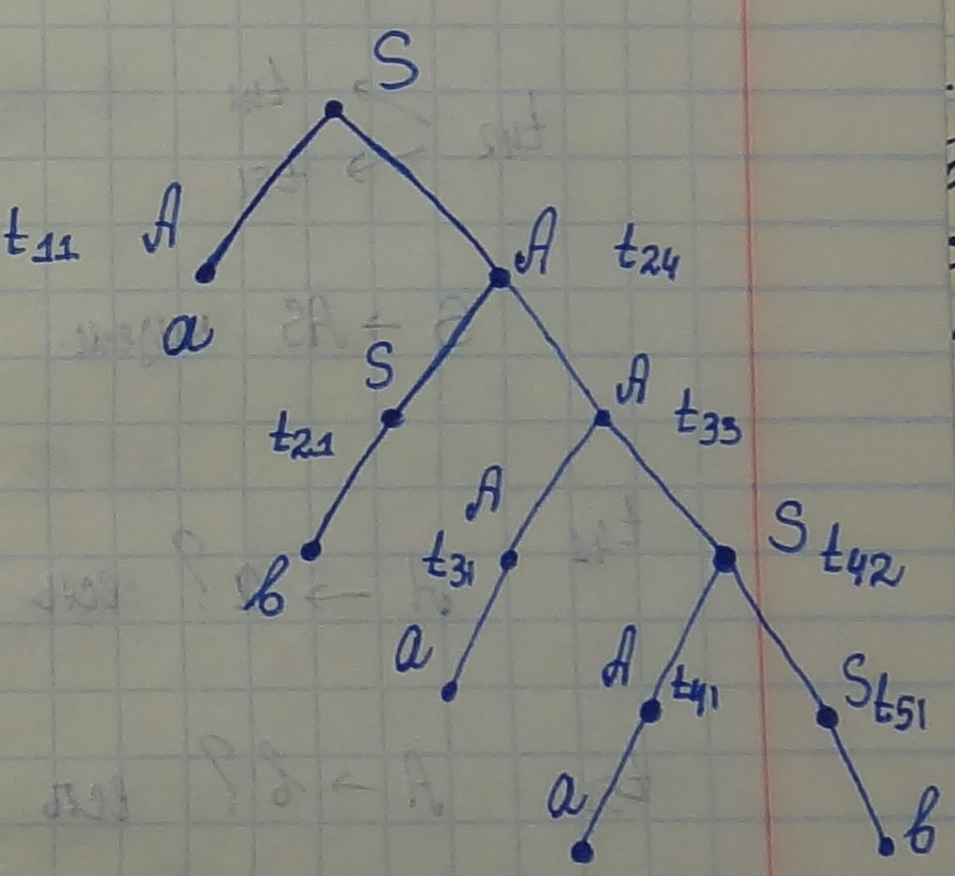
Как могли получить t₂₄?

t₂₄ -> t₂₁ t₂₄ -> t₃₃ t₂₄ -> t₂₂ t₂₄ -> t₄₂ t₂₄ -> t₂₃ t₂₄ -> t₅₁

Имея дерево вывода, можно построить разбор.

A -> …

t₃₃ -> t₃₁ A

t₃₃ -> t₄₂ S,A

t₃₃ -> t₃₂

t₃₃ -> t₅₁

Ищем правила A -> AS №5 правило, A -> AA

t₄₂ S -> …

t₄₂ -> t₄₁

t₄₂ -> t₅₁

S -> AS, ищем №2 правило

t₄₁ A -> a? есть

t₅₁ A -> b? есть

Трудоемкость построения дерева по таблице

Т_дер(n) = O(n²)

Чтобы найти правило, нужно проделать O(n) операций.

Каждая вершина имеет степень, не превосходящую 3.

Листьев дерева n.

deg (лист) = 1, их n

deg (корень) = 2, их 1

Остальные вершины deg = 3, их x-n-1

x – число всех вершин деревьев вывода.

Сложим степени всех вершин = <2 x число ребер>

3(x–n-1) + n + 2 = 2m;

2m = 2(x-1), т.к. дерево.

x = 2n + 1

Число правил в дереве = x-n = n+1, отсюда трудоемкость построения разбора O(n²)

Трудоемкость алгоритма O(n³)

Если грамматика с однозначным выводом, то O(n²)

Если язык детерминированный O(n)