
- •1.Операции над словами и языками. Понятие грамматики и грамматического вывода.
- •2.Иерархия Хомского формальных языков.
- •3. Понятия конечного автомата и конечно-автоматного языка. Примеры конечно-автоматных языков.
- •4.Детерминированные и недетерминированные конечные автоматы. Алгоритм детерминизации недетерминированного конечного автомата.
- •5. Алгоритм минимизация конечного автомата.
- •7. Лемма Огдена (о разрастании) для конечно-автоматных языков. Пример языка, не являющегося конечно-автоматным.
- •8. Правила построения регулярных выражений. Теорема Клини о совпадении классов конечно-автоматных и регулярных языков.
- •9. Алгоритм анализа конечного автомата.
- •10. Алгоритм синтеза конечного автомата.
- •11. Свойства замкнутости праволинейных языков относительно теоретико-множественных операций, конкатенации и итерации.
- •12. Решение систем линейных уравнений с регулярными коэффициентами. Описание праволинейного языка с помощью системы линейных уравнений с регулярными коэффициентами.
- •13. Теорема о совпадении классов праволинейных, конечно-автоматных и регулярных языков.
- •14. Определение контекстно-свободной грамматики. Контекстно-свободный грамматический вывод, левый и прявый выводы. Примеры кс-языков. Деревья вывода.
- •15. Приведенная форма кс-грамматики, алгоритм преобразования кс-грамматики к приведенной форме.
- •16. Лемма Огдена для кс-языков. Пример языка, не являющегося контекстно-свободным.
- •21. Соотношение между кс-языками и языками, допускаемыми мпа. Построение по кс-грамматике мп-автомата.
- •22. Понятие мп-преобразователя. Нисходящие и восходящие распознаватели.
- •23. Построение мп-преобразователя, реализующего левый разбор
16. Лемма Огдена для кс-языков. Пример языка, не являющегося контекстно-свободным.
Пусть есть некоторое слово α, |α|=к.
Позиция i – натуральное число 1≤i≤k, буква а занимает позицию i в α, α=α1аα2, |α1|=i-1. Символ а занимает I позицию в слове α.
Формулировка:
Для любой КС-грамматики G=<VT, VN, P, S> существует такое к≥1, что если αϵL(G), |α|≥к и в α выделены ≥ к различных позиций, то α можно записать в виде:
α=uvwxy, причем
1.w содержит хотя бы одну выделенную позицию
2.либо u и v обе содержат выделенную позицию, либо x и y обе содержат выделенную позицию (хотя бы одно из этих условий обязательно выполняется)
3.v w x содержит не более к выделенных позиций
4. существует нетерминал А, что
S=>+uAy=>+uvAxy=>+…=>+uviAxiy=>+uviwxiy
Следствие леммы Огдена (леммы о разрастании)
Пусть L – КС-язык, тогда существует константа л≥1, что если αϵL, |α|≥k, то α можно представить в виде:
Α=uvwxy, где любое слово вида uviwxiy для любого i≥0.
Пример языка, не являющегося КС.
L={anbncn|nϵ натур.}. Показать, что L-не КС.
Сущ-ет к≥1, α= aкbкcк, |α|>к, по лемме aкbкcк= uvwxy, где vx≠λ, |vwk|≤k =>vwx не может содержать все буквы алфавита.
ак – префикс u
ск – входит в у
uviwxiy ϵ L при i≥0
Пусть i=0 => u w y ϵ L
т.к. |vx|≠λ => выкинули либо букву а, либо b, либо с =>нарушается равенство степеней n, не получаем равенства количества букв в обоих случаях. Наше предположение не верно, L – не КС-язык.
21. Соотношение между кс-языками и языками, допускаемыми мпа. Построение по кс-грамматике мп-автомата.
Соотношение между КС-языками и языками, допускаемыми МПА.
Теорема
Класс языков порождаемых КС-грамматиками, совпадает с классом языков, допускаемых МП-автоматами.
Это означает, что для любой КС-грамматики можно построить автомат с магазинной памятью, допускающий тот же язык.
Построение по КС-грамматике МП-автомата.
Пусть
дана грамматика: ![]() .
Автомат строится так, что он моделирует
левые выводы грамматики.
.
Автомат строится так, что он моделирует
левые выводы грамматики.
![]() всегда строим автомат, допускающий
опустошение магазина.
всегда строим автомат, допускающий
опустошение магазина.
Под
![]() подразумевается:
подразумевается:
Если множество правил R содержит:
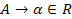 ,
то
,
то  ,
если верхний символ в магазине не
терминал, то не читая слова, заменяем
его в магазине на
,
если верхний символ в магазине не
терминал, то не читая слова, заменяем
его в магазине на 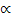 .
.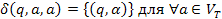
Пример:
![]()
q |
|
z |
|
q |
|
|
|
q |
|
|
|
q |
|
|
|
q |
|
|
|
22. Понятие мп-преобразователя. Нисходящие и восходящие распознаватели.
МП-преобразователи
![]()
![]() (множество
подмножеств)
(множество
подмножеств)
Т.е. записывается на выходную ленту ещё и слово в алфавите В.
![]() где:
где:
x- принадлежит замыканию А` слово которое ещё не прочитано на входной ленте.
– слово в магазине.
у – слово записанное в данный момент на входной ленте.
Вид преобразования:
![]()
Одна
конфигурация перейдёт в другую за один
такт, если ![]()
![]()
Левый разбор – последовательность номеров правил грамматики, образующих левый вывод.
Нисходящий разбор – каждому дереву вывода соотвествует лувый разбор.
Пусть известен корень дерева вывода и его крона.
Дерево постепенно разворачивается, начиная от корня. Пытаемся к корню применить какое-либо правило грамматики, затем к самому левому нетерминалу и т.д.
Получим разбор построим дерево вывода.
Нисходящий разбор производится с помощью преобразователя с МП.
![]()
Hl-левый анализатор.
Идея аналогична МП-автомату, строящему такой же язык, как на входе и плюс к этому записывающий номера правил.
![]() (опустошение магазина допускается)
(опустошение магазина допускается)
 ,
,
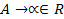 ,
i – номер правила.
,
i – номер правила.
Если верхний символ из терминального алфавита , он стирается и на выходную ленту ничего не падается.
