
- •1. Числ ряды
- •2.Действия над рядами Св-ва
- •3. Необх признак сх
- •6. Ряды с неотр Признаки сравнения
- •7. Признак Даламбера.
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •9. Интегральный признак Коши.
- •10.Знакпер ряд абс и услвн сх
- •12. Знакчеред ряды Лейбниц
- •14. Функ ряды область сх
- •15. Равн сх фр Вейерштрассе
- •17. Степ ряд Абель
- •25. Решение ду
- •27 Тригон ряд фурье
- •32. Разлож непериод функ
- •33. Тригоно ряд фурье в комп форме
- •34. Интеграл фурье
- •35 Комп форма инт фурье
- •36. Опред фкп
- •37. Предел и непрерывн фкп
- •42. Общая степен
- •43. Условие коши-риманна
- •47. Основн теор коши
- •48. Интегр формула коши
- •49. Фкп в комп области степ ряд
- •50. Ряд тейлора в фкп
- •51. Ряд лорана фкп
- •52. Особые точки
- •53. Вычеты
- •54. Основн теор вычет
- •55. Вычисл вычет интегр
- •57. Теор подобия смещен опереж
- •58. Ди и инт изобр
- •59. Свертка
27 Тригон ряд фурье
Тригонометрическим рядом - называется функциональный ряд вида
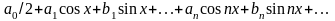 т.е.
т.е.
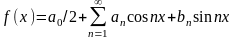 (1)
(1)
Где
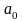 ,
,
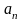 ,
,
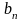 (n=1,2,…)называются
коэффициентами ряда.
(n=1,2,…)называются
коэффициентами ряда.
Будем считать, что ряд равномерно сходится. Интегрируем правую и левую части:
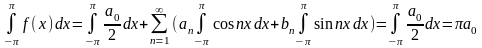
Отсюда:
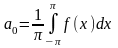
Домножим
обе части равенства (1) на
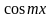 и
проинтегрируем обе части:
и
проинтегрируем обе части:
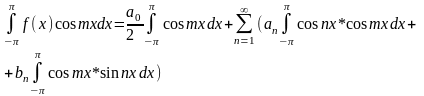
При
m=n
получим:
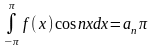
Отсюда:
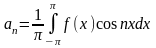 ,
n=1,2,3,…
,
n=1,2,3,…
Аналогично,
умножив равенство (1) на
 и проинтегрировав почленно на отрезке
[
и проинтегрировав почленно на отрезке
[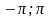 ],
найдём
],
найдём
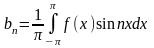 ,
n=1,2,3,…
,
n=1,2,3,…
28. теор дирихле. сдвиг
Если f(x) непрерывна или кусочно-непрерывна на отрезке [-π,π], то ряд Фурье этой ф-ии сходиться к ней в точках непрерывности, а в точках разрыва ф-ии его сумма выражается след. образом S(x0)=(f(x0-0)+ f(x0+0))/2 (без док-ва)
29.Разложен четн функ
1. Пусть ф-ция f(x) – четная, т. е. f(-x)=f(x).
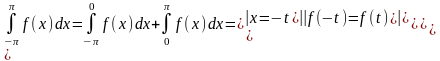
Значит:
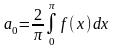 ;
;
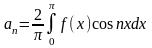 ;
;
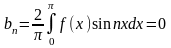 .
.
Ряд Фурье для четных ф-ций – ряд только по косинусам
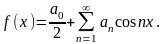
30. Разлож нечетн функ
Пусть ф-ция f(x) – нечетная, т. е. f(-x)=-f(x).
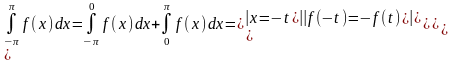
Значит:
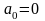 ;
;
 ;
;
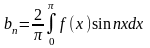 .
.
Ряд Фурье для четных ф-ций – ряд только по синусам

31. Ряд фурье для период 2л
Пусть f(х) есть периодическая функция с периодом 2l, вообще говоря, отличным от 2π. Разложим ее в ряд Фурье.
Сделаем замену
переменной по формуле:
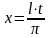 .
.
Тогда функция
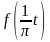 будет периодической функцией от t
с периодом 2π. Ее можно разложить в ряд
Фурье на отрезке
будет периодической функцией от t
с периодом 2π. Ее можно разложить в ряд
Фурье на отрезке
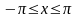 :
:
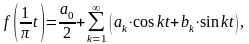 где
где
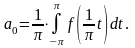
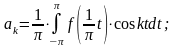
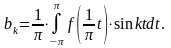
Возвратимся теперь к старой переменной х:
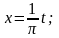
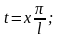
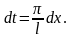
Тогда будем иметь:
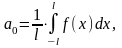
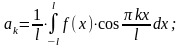
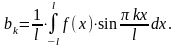
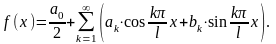
32. Разлож непериод функ
Пусть ф-ция f(x) непереодич., заданная на [a,b].
Вместо функции
f(x)
рассматривают ф-цию
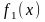 с периодом 2l,
причем [a,b]
с периодом 2l,
причем [a,b]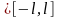 и на [a,
b]
ф-ция
совпадает
с функцией f(x).
и на [a,
b]
ф-ция
совпадает
с функцией f(x).
Поскольку функция периодическая то ее разлагают в ряд Фурье.
Рассмотрим один важный случай: пусть функция f(x) задана на интервале (0, l) . Ее надо доопределить на интервале (-l , 0). Можно доопределить четным образом. В этом случае мы получаем ряд Фурье только по косинусам.
Можно доопределить нечетным образом. Получим ряд Фурье только по синусам.
33. Тригоно ряд фурье в комп форме
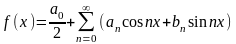 ;
;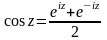 ;
;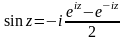 ;
;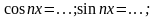
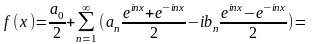
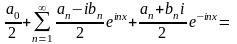
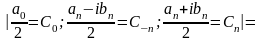
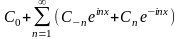 интеграл
Ф. В комплексной формуле при (
интеграл
Ф. В комплексной формуле при (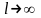 ):
):
34. Интеграл фурье
Пусть
имеем f(x),
определенную на (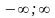 )
и абсолютно интегрируемую на этом
интервале,т.е.
)
и абсолютно интегрируемую на этом
интервале,т.е.
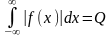 (конечное
число),фун-ция разлагается в ряд на
(-l,l).
(конечное
число),фун-ция разлагается в ряд на
(-l,l).
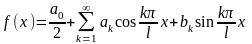 ;
;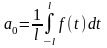 ;
;
 ;
;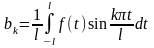
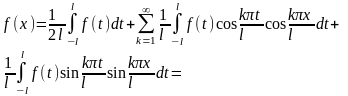
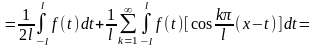 |
|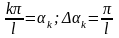 |=
|=
(Умножим
и поделим на
 )=
)=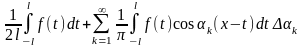
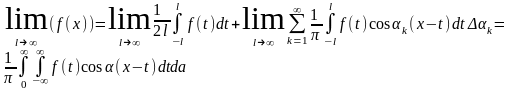 (1)
(1)
(1)- Интеграл Фурье
Если ф-ция четная или нечетная, то частные случаи:
Распишем
интеграл: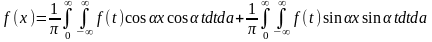
1)f(x)-четная
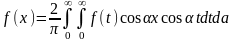
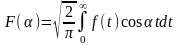 -
cos
преобразование Фурье
-
cos
преобразование Фурье
2)f(x)-нечетная
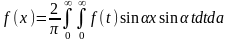
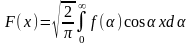 -
обратное преобразование от cos
преобразования
-
обратное преобразование от cos
преобразования
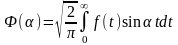 -
sin
преобразование Фурье
-
sin
преобразование Фурье
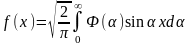 -
обратное преобразование sin
преобразование Фурье
-
обратное преобразование sin
преобразование Фурье
