
- •1. Числ ряды
- •2.Действия над рядами Св-ва
- •3. Необх признак сх
- •6. Ряды с неотр Признаки сравнения
- •7. Признак Даламбера.
- •3) В случае ответа о сходимости или расходимости ряда теорема не дает.
- •9. Интегральный признак Коши.
- •10.Знакпер ряд абс и услвн сх
- •12. Знакчеред ряды Лейбниц
- •14. Функ ряды область сх
- •15. Равн сх фр Вейерштрассе
- •17. Степ ряд Абель
- •25. Решение ду
- •27 Тригон ряд фурье
- •32. Разлож непериод функ
- •33. Тригоно ряд фурье в комп форме
- •34. Интеграл фурье
- •35 Комп форма инт фурье
- •36. Опред фкп
- •37. Предел и непрерывн фкп
- •42. Общая степен
- •43. Условие коши-риманна
- •47. Основн теор коши
- •48. Интегр формула коши
- •49. Фкп в комп области степ ряд
- •50. Ряд тейлора в фкп
- •51. Ряд лорана фкп
- •52. Особые точки
- •53. Вычеты
- •54. Основн теор вычет
- •55. Вычисл вычет интегр
- •57. Теор подобия смещен опереж
- •58. Ди и инт изобр
- •59. Свертка
17. Степ ряд Абель
Если степенной
ряд сходится при некотором значении
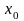 ,
не равном нулю, то он абсолютно сходится
при всяком х, для которого
,
не равном нулю, то он абсолютно сходится
при всяком х, для которого
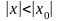 .
.
Если ряд расходится
при некотором значении
,
то он расходится при всяком х, для
которого
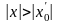 .
.
Доказательство:
Так как по предположению числовой ряд
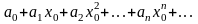 сходится, то его общий член
сходится, то его общий член
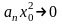 при
,
а это значит, что существует такое
положительное число М, что все члены
ряда по абсолютной величине меньше М.
Перепишем ряд в виде
и
рассмотрим ряд из абсолютных величин
его членов:
при
,
а это значит, что существует такое
положительное число М, что все члены
ряда по абсолютной величине меньше М.
Перепишем ряд в виде
и
рассмотрим ряд из абсолютных величин
его членов:
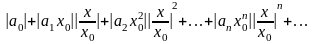 Члены
этого ряда меньше соответствующих
членов ряда
Члены
этого ряда меньше соответствующих
членов ряда
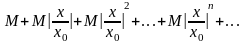
При
последний ряд представляет собой
геометрическую прогрессию со знаменателем
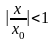 и, следовательно, сходится.
и, следовательно, сходится.
Теперь нетрудно
доказать и вторую часть теоремы: пусть
в некоторой точке
ряд
расходится. Тогда он будет расходиться
в любой точке х, удовлетворяющей условию
.
Действительно, если бы в какой-либо
точке х-, удовлетворяющей этому условию,
ряд сходился, то в силу только что
доказанной первой части теоремы он
должен был бы сходиться и в точке
,
так как
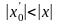 .
Но это противоречит условию, что в точке
ряд расходится. Следовательно, ряд
расходится и в точке х.
.
Но это противоречит условию, что в точке
ряд расходится. Следовательно, ряд
расходится и в точке х.
18.Интервал и радиус сх
Интервалом сходимости степенного ряда является такой интервал от –R до R, что для всякой точки х, лежащей внутри этого интервала, ряд сходится и притом абсолютно, а для точек х, лежащих вне его, ряд расходится. Число R называют радиусом сходимости степенного ряда.
20. Ряды Тейлора и маклорена
Пусть ф-я f(x) является бесконечно диффериенцируемой, тогда этой ф-и можно поставить в соответствие ряд
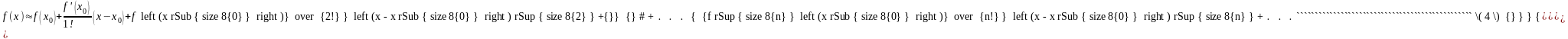
Когда x00,
то
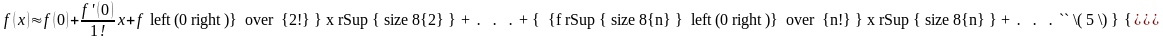
В интервале сходимости (-R;R) сумма этого ряда S(x), но не всегда f(x)=S(x).
Если ряд сходится, то его можно представить в виде Sn(x)+rn(x) Pn(x)+Rn(x) и Sn(x)=Pn(x), значит rn(x)=Rn(x) иначе не равны.
21. Теор о ед разлож в ряд Тейлора
Если все производные ограничены одной и той же константой, то ряд Тейлора сходится к ф – и по x.
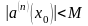
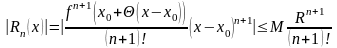
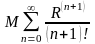 - сходится по
признаку Даламбера.
- сходится по
признаку Даламбера.
У сходящегося
общий член ряда
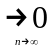
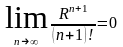 ,
отсюда следует, что
,
отсюда следует, что
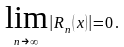
Пусть f(x) бесконечно дифференцируема и
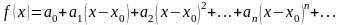 Является
ли этот ряд рядом Тейлора?
Является
ли этот ряд рядом Тейлора?
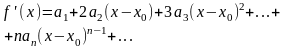
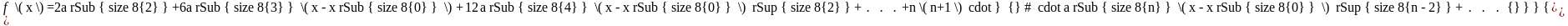
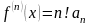 .
.
Пусть x=x0,
тогда
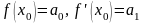 ,
,
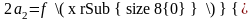 или
или
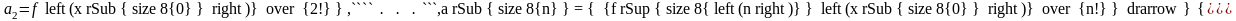
f(x) – ряд Тейлора.
24. Прибл выч интегралов
В зависимости от
того, с какой точностью требуется
вычислить
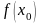 оставляют достаточное число членов
этого числового ряда. Достаточное число
слагаемых берут из оценки достаточного
члена ф-лы Тейлора или ост члена ряда
Тейлора. Либо для знакочередуюшегося
ряда, используя следствие из признака
Лейбница.
оставляют достаточное число членов
этого числового ряда. Достаточное число
слагаемых берут из оценки достаточного
члена ф-лы Тейлора или ост члена ряда
Тейлора. Либо для знакочередуюшегося
ряда, используя следствие из признака
Лейбница.
Для вычисления
определенных интегралов
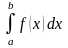
Подинтегральную ф-цию разлагают в ряд Маклорена и в области равномерной сходимости возможно почленное интегрирование
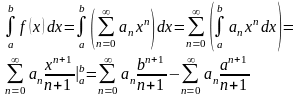
25. Решение ду
Пусть требуется решить ур-е
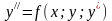 (1)
(1)
удовл.условиям
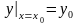 ,
,
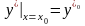 (2)
(2)
Реш-е
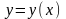 ур-я (1) ищем в виде ряда Тейлора
ур-я (1) ищем в виде ряда Тейлора
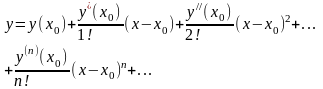 (3)
(3)
при
этом первые 2 коэффициента находим из
нач. условий (2). Подставив в ур-е (1)
значения
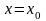 ,
,
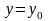 ,
,
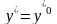 находим
3-ий коэффициент:
находим
3-ий коэффициент:
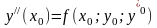 Значения
Значения
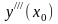 ,
,
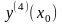 ,…находим
путем последоват.дифференцирования
ур-я (1) по X
и вычиления производных при
(коэффициентов), их подставляем в
равенство (3). Ряд ( 3) представляет искомое
частное реш-е ур-я (1) для тех значений
X,
при к-рых он сходится. Частичная сумма
этого ряда будет приближенным реш-ем
ДУ (1).
,…находим
путем последоват.дифференцирования
ур-я (1) по X
и вычиления производных при
(коэффициентов), их подставляем в
равенство (3). Ряд ( 3) представляет искомое
частное реш-е ур-я (1) для тех значений
X,
при к-рых он сходится. Частичная сумма
этого ряда будет приближенным реш-ем
ДУ (1).
