
- •Исчисления высказываний
- •Определение формального исчисления
- •Исчисление высказываний генценовского типа
- •Эквивалентность формул
- •Нормальные формы
- •Семантика исчисления секвенций
- •Исчисление высказываний гильбертовского типа
- •Алгоритмы проверки общезначимости и противоречивости в ив
- •Логика и исчисления предикатов
- •Алгебраические системы. Формулы сигнатуры σ. Истинность формулы на алгебраической системе
- •Секвенциальное исчисление предикатов
- •Эквивалентность формул в
- •Нормальные формы
- •Теорема о существовании модели
- •Исчисление предикатов гильбертовского типа
- •Скулемизация алгебраических систем
- •Метод резолюций в исчислении предикатов
- •Некоторые проблемы аксиоматического исчисления предикатов
- •Разрешимость
- •Непротиворечивость и независимость
- •Полнота в узком смысле
- •Полнота в широком смысле
- •Элементы теории алгоритмов
- •Машины Тьюринга
- •Функции, вычислимые на машинах Тьюринга.
- •Рекурсивные функции и отношения
- •Примитивно рекурсивные функции.
- •Примитивно рекурсивные отношения.
- •Частично рекурсивные функции.
- •Рекурсивно перечислимые отношения
- •Неразрешимость исчисления предикатов. Теорема Геделя о неполноте. Разрешимые и неразрешимые теории.
Исчисление высказываний генценовского типа
Определим элементы исчисления высказываний ИС.
Алфавит ИС состоит из букв А, В, Q, Р, R и других, возможно, с индексами (которые называются пропозициональными переменными), логических символов (связок) отрицания , конъюнкции , дизъюнкции , импликации →, следования ├·, а также вспомогательных символов: левой скобки (, правой скобки ), запятой ,.
Множество формул ИС определяется индуктивно: Слово алфавита ИС называеся формулой, если:
все пропозициональные переменные являются формулами ИС (такие формулы называются элементарными или атомарными)
если φ, ψ — формулы ИС, то φ, (φψ), (φψ), (φ→ψ) - формулы ИС;
выражение является формулой ИС тогда и только тогда когда это может быть установлено с помощью пунктов "а" и "б"
В дальнейшем при записи формул будем опускать некоторые скобки, используя те же соглашения, что и в алгебре логики.
Определение. Подформулой ψ формулы φ ИС будем называть подслово φ, являющееся формулой ИС.
Если
все вхождения подформулы
ψ
в
φ
заменить
на формулу
![]() ,
то получим новую формулу
,
то получим новую формулу
![]() .
.
Предложение
1. Каждая
неатомарная формула
![]() в ИС представима в одном и только одном
из следующих видов
в ИС представима в одном и только одном
из следующих видов
![]() для однозначно определенных
для однозначно определенных
![]() и
.
и
.
Секвенциями называются конечные выражения следующих: двух видов, где φ1,…,φn, ψ ― формулы ИС:
φ1,…,φn ├ψ (говорится "из истинности φ1,…,φn логически следует ψ”),
φ1,…,φn├ (говорится "система формул φ1,…,φn противоречива")
Последовательности формул φ1,…,φn в секвенциях будут часто обозначаться через Г (возможно, с индексами): Г├ψ, Г├ .При этом последовательность Г считается пустой при n=0. Значит, записи ├ψ и ├ также являются секвенциями, первая которых может читаться как утверждение о доказуемости формулы ψ.
Таким образом, наряду с формулами, символизирующими простые или сложные высказывания, секвенции являются записями утверждений, в которых выделяются посылки и заключение. Буквы , , будем называть переменными для формул; добавим их к алфивиту ИС и обозначим через В.
Определение. Схемой секвенций (формул) ИС будем называть такое слово в алфавите В, что при любой подстановке в это слово вместо переменных формул соответствующих конкретных формул, получим секвенцию (формулу) ИС. Результат подстановки будем называть частичным случаем этой схемы.
Пример.
![]() -
схема,
-
схема,
![]() -
результат
подстановки, где
-
результат
подстановки, где
![]() .
.
Множество аксиом ИС определяется следующей схемой секвенций. φ├φ, где φ ― произвольная формула ИС.
Аксиомами являются, например, секвенции Α→ A→BC├ Α→ A→BC.
Правилa вывода ИС (формализуют стандартные логические способы рассуждений) задаются следующими записями, где Г — произвольная (возможно пустая) конечная последовательности формул ИС, φ,ψ,χ — произвольные формулы ИС.
 (введение
Λ).
(введение
Λ).
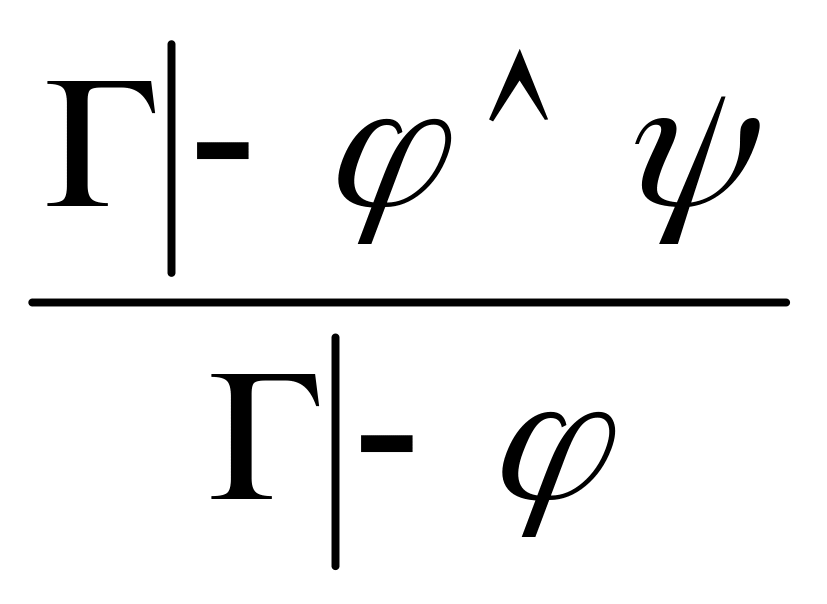 (удаление
).
(удаление
).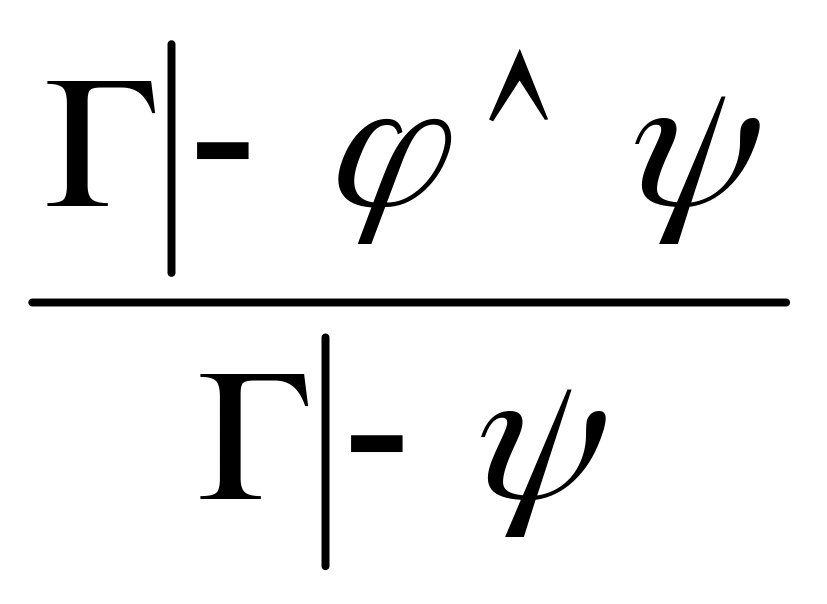 (удаление
).
(удаление
).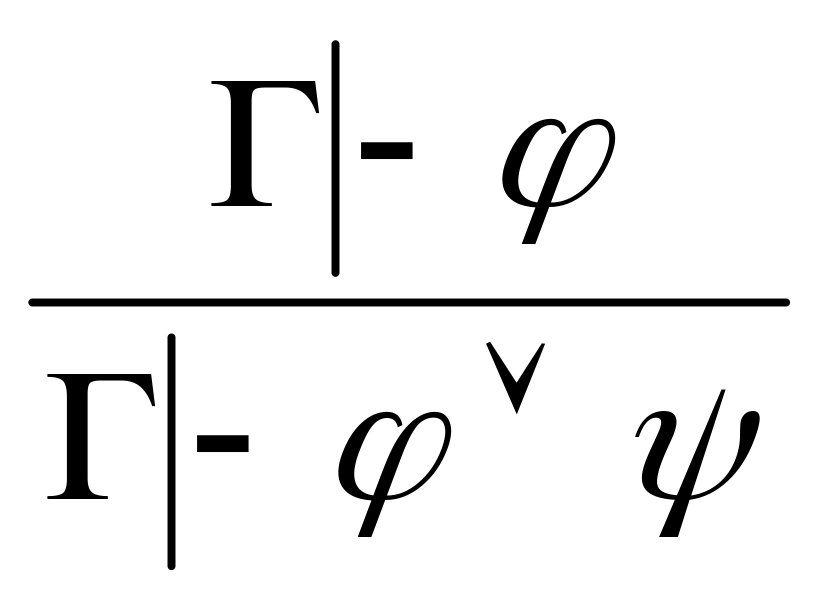 (введение
).
(введение
).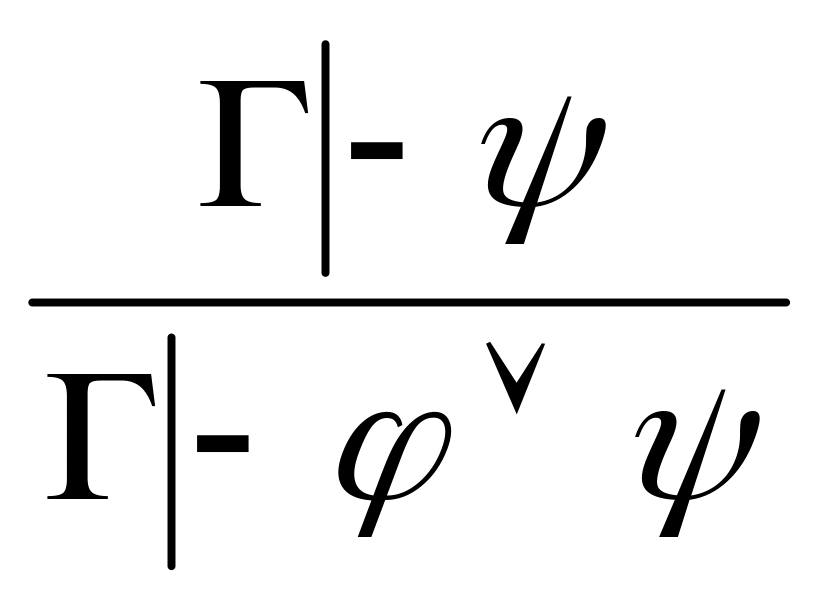 (введение
).
(введение
).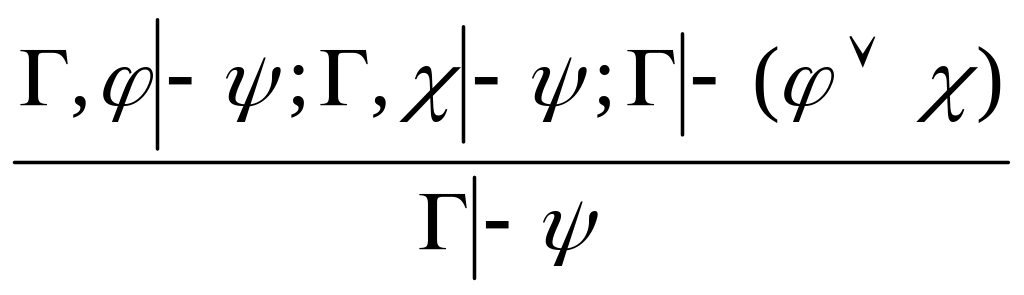 (удаление
,
или правило разбора двух случаев).
(удаление
,
или правило разбора двух случаев).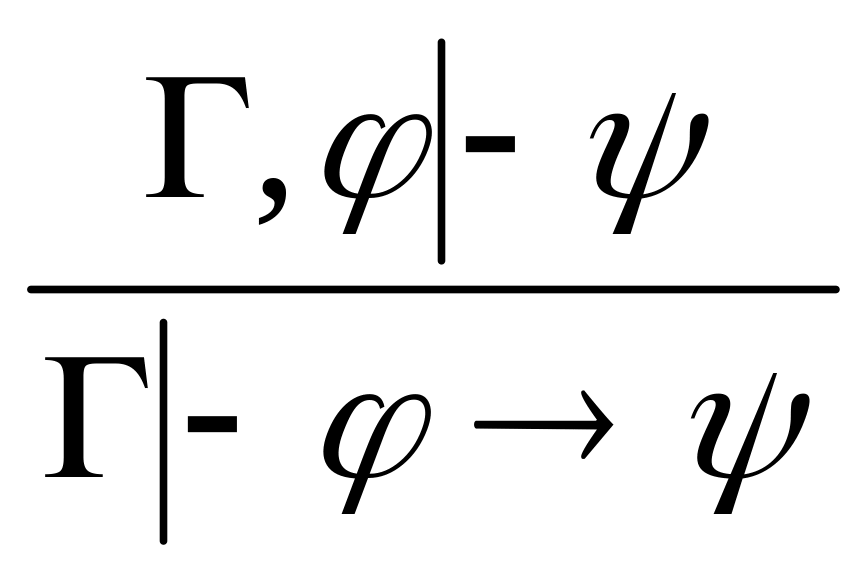 (введение
→) – правило эквивалентной переформулировки
теорем. Когда условие теоремы перемещается
в заклячение в виде посылки.
(введение
→) – правило эквивалентной переформулировки
теорем. Когда условие теоремы перемещается
в заклячение в виде посылки.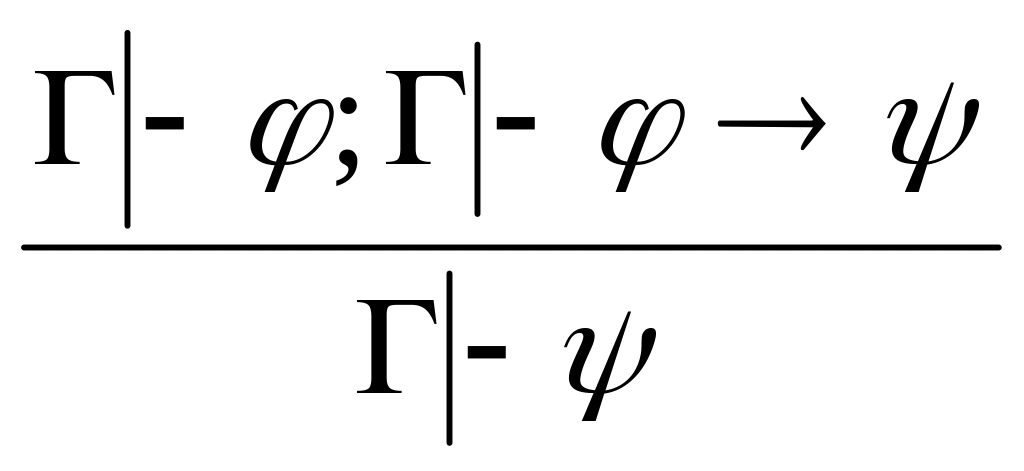 (удаление
→) – правило отделения, modus
ponens.
(удаление
→) – правило отделения, modus
ponens.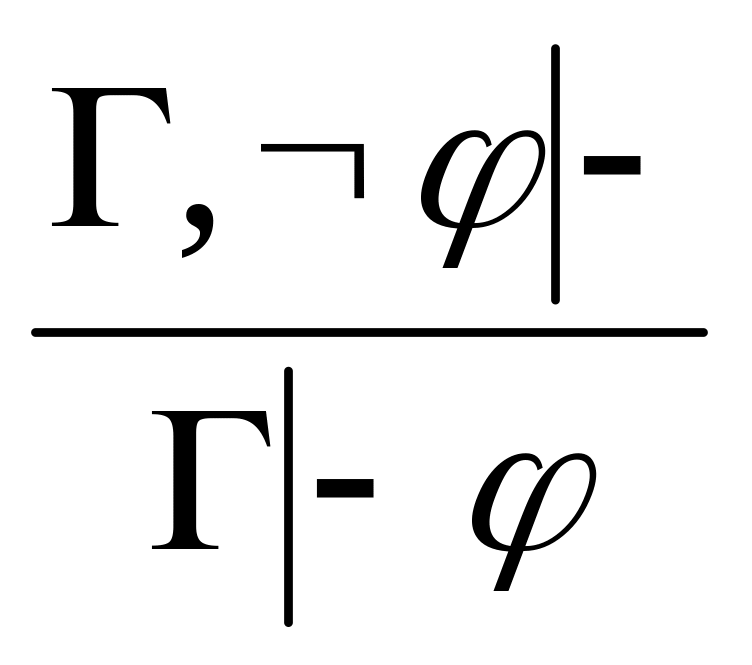 (удаление
,
или
доказательство от противного).
(удаление
,
или
доказательство от противного).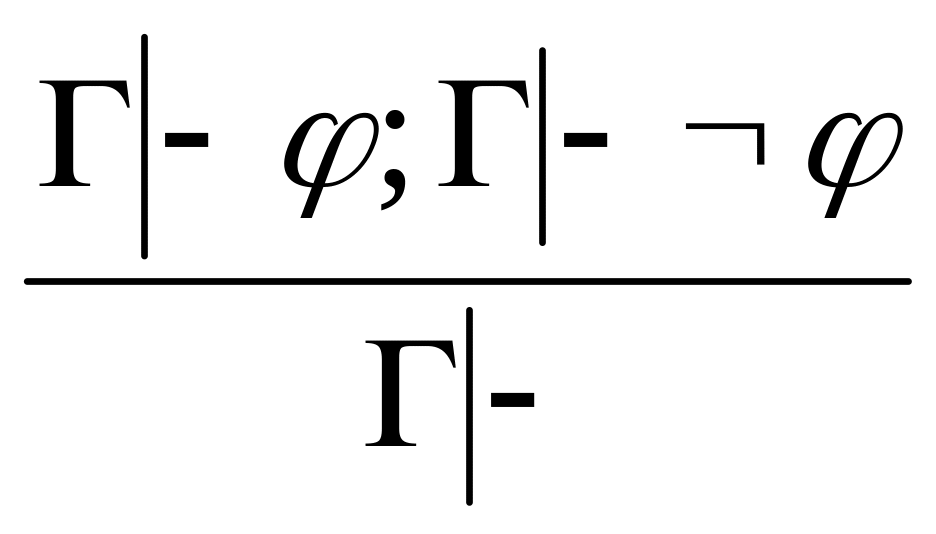 (выведение
или обнаружения противоречия)
(выведение
или обнаружения противоречия) (перестановка
посылок).
(перестановка
посылок).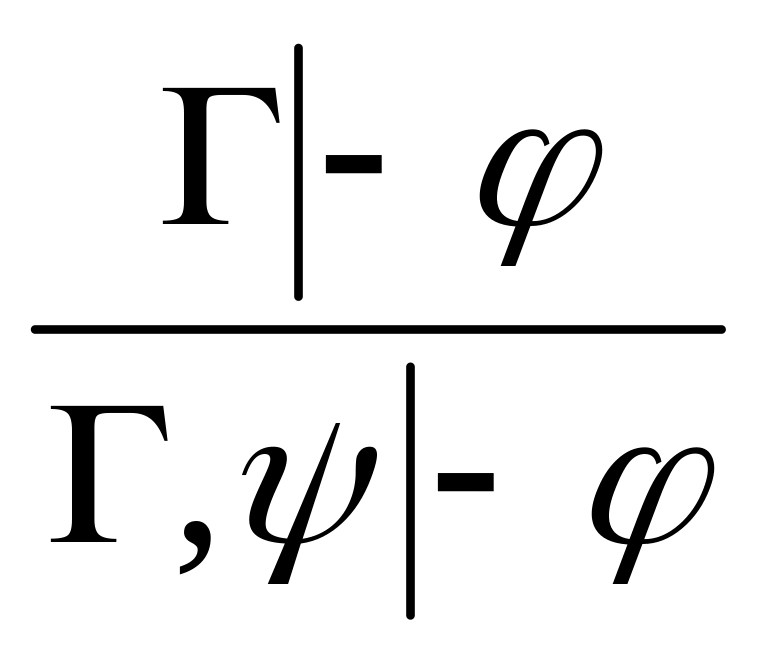 (утончение,
или правило лишней посылки) – добавление
условий не влияет на вывод.
(утончение,
или правило лишней посылки) – добавление
условий не влияет на вывод.
Вывод
S0,..
Sn,
-
в ИС
называется линейным
доказательством.
Секвенция
S
называется
доказуемой
в
ИС, или теоремой
ИС,
если существует линейное доказательство
So,..,Sn
в
ИС, заканчивающееся
секвенцией S:
Sn
= S
Формула
φ
называется
доказуемой
в
ИС, если в ИС доказуема секвенция ├φ
. Если
![]() - доказательство в ИС,
- доказательство в ИС,
![]() -
также, тогда
,
- тоже доказательство ИС.
-
также, тогда
,
- тоже доказательство ИС.
Определим по индукции понятие дерева секвенций:
любая секвенция является деревом секвенций;
если Do, …,Dn — деревья секвенций и S — секвенция, то запись
![]()
также является деревом секвенций;
любое дерево секвенций строится в соответствии с пп. 1 и 2.
Вхождением секвенции в дерево D называется место, которое секвенция занимает в дереве. Каждая секвенция может иметь несколько вхождений в дерево секвенций. Вхождение секвенции дерево D, над (под) которым нет горизонтальной черты, называется начальным (соответственно заключительным).
Из определения дерева секвенций ясно, что начальных секвенций в дереве может быть несколько, а заключительная секвенция единственна.
Часть дерева, состоящая из секвенций, находящихся непосредственно над некоторой чертой, под той же чертой, а также самой черты, называется переходом.
Дерево D называется доказательством в ИС в виде дерева, если все его начальные секвенции суть аксиомы ИС, а переходы осуществляются по правилам 1-12. Дерево D называется доказательством секвенции S в виде дерева в ИС, или деревом вывода S в ИС, если D — доказательство в ИС и S — его заключительная секвенция.
Покажем, что наличие линейного доказательства секвенции равносильно существованию доказательства секвенции в виде дерева.
Предложение 1. Секвенция S имеет доказательство в ИС в виде дерева тогда и только тогда, когда S ― теорема ИС.
Доказательство. Пусть S0,..., Sn-1, S ― линейное доказательство в ИС. Если S ― аксиома, то S ― доказательство секвенции S в виде дерева. Предполагая по индукции, что секвенции S0,..., Sn-1 имеют доказательства D0,..., Dn-1 в виде дерева, а секвенция S получается из секвенций Si1,..., Sik применением некоторого правила вывода, заключаем, что дерево
![]()
является доказательством секвенции S в виде дерева.
Пусть теперь дано доказательство секвенции S в виде дерева D. Если S ― аксиома, то S является линейным доказательством секвенции S. Допустим, что секвенция S не является аксиомой. Тогда дерево D имеет вид
где Di=Si или ,
i = 0,...,п. Предполагая по индукции, что секвенции Si имеют линейные доказательства Li, i= 0,...,п, получаем линейное доказательство L0, ..., Ln, S секвенции S.
Очевидно, что представление доказательства в виде дерева более наглядно и позволяет проследить все переходы по правилам вывода.
Пример 1. Приведем доказательство секвенций φψ├ψφ в виде дерева для любых формул φ и ψ.
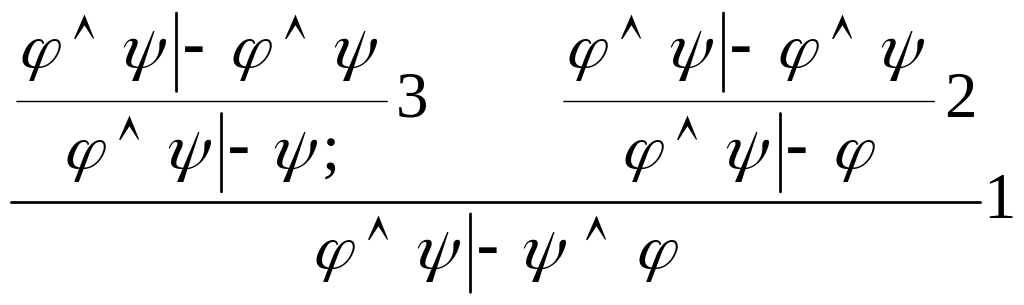
2. Следующее дерево демонстрирует доказуемость формулы φφдля любой формулы φ:
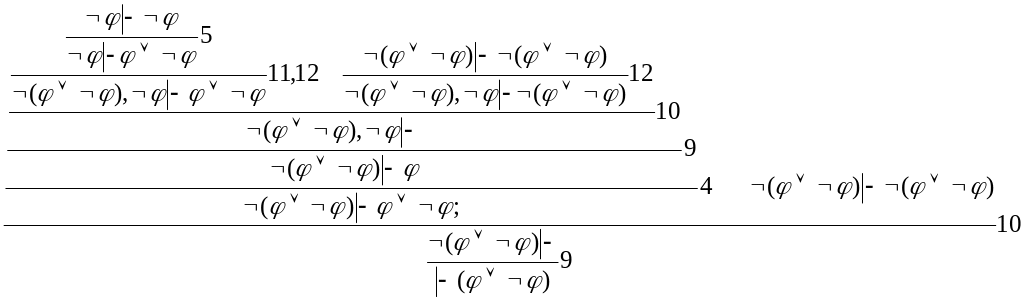
Правило
![]() называется
допустимым
в
ИС, если из выводимости в ИС секвенций
S0,...,
Sn
следует выводимость в ИС
секвенции S.
называется
допустимым
в
ИС, если из выводимости в ИС секвенций
S0,...,
Sn
следует выводимость в ИС
секвенции S.
Заметим, что допустимость правила равносильна тому, что его добавление в исчисление ИС не расширяет множество доказуемых секвенций.
Предложение 2. Следующие правила допустимы в ИС:
(а) ![]() (расширение
посылок);
(расширение
посылок);
(б) ![]() (расширение посылок);
(расширение посылок);
где
в пп. (а) и (б) выполняется
![]()
(в) ![]() (сечение);
(сечение);
(г) ![]() (объединение
посылок);
(объединение
посылок);
(д) ![]() (расщепление
посылок);
(расщепление
посылок);
(е) ![]() (разбор
случаев)
(разбор
случаев)
(ж) ![]() (выведение
противоречия)
(выведение
противоречия)
(з) ![]() (выведение
из противоречия)
(выведение
из противоречия)
(и) ![]() (контрапозиция);
(контрапозиция);
(к) ![]() (контрапозиция);
(контрапозиция);
(л) ![]() (контрапозиция);
(контрапозиция);
(м) ![]() (доказательство
от противного);
(доказательство
от противного);
(н) ![]() (введение
,
→);
(введение
,
→);
(о) ![]() (удаление
,
→)
(удаление
,
→)
Доказательство.
Допустимость правила
![]()
показывается следующим деревом:
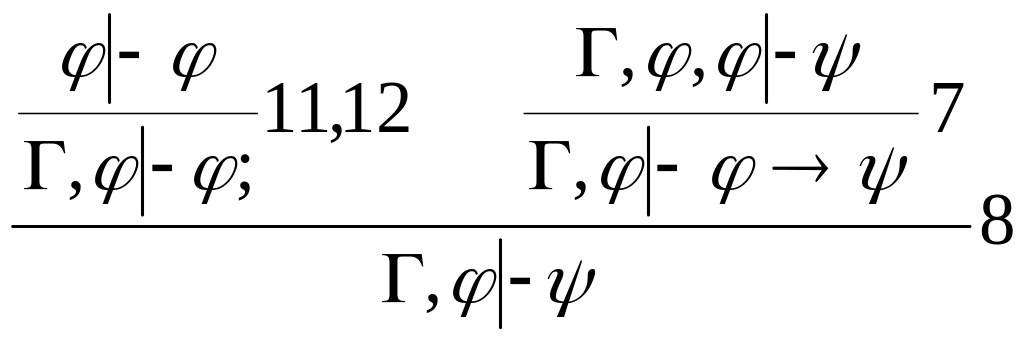
Допустимость правила (а) следует из допустимости указанного правила с помощью правил 11 и 12. Допустимость правила (б) вытекает из правил (а), (ж) и (з).
Докажем допустимость правила (з), а остальные правила оставим студентам в качестве упражнения

устанавливает доказуемость секвенции Г├φ.
Использование допустимых правил вывода позволяет во многих случаях приводить сокращенные доказательства секвенций, которые при необходимости можно преобразовать в доказательства секвенций в виде деревьев в ИС.
Например, следующее дерево устанавливает доказуемость секвенции (φ→ψ),ψ├φ:
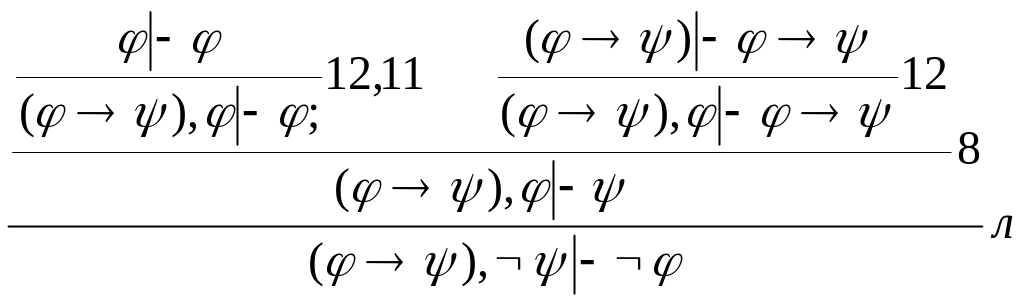
Правило называется равносильным, если доказуемость (единственной) секвенции, стоящей над чертой, равносильна доказуемости секвенции, стоящей под чертой. Из предложения 1.2.2 вытекает, что следующие правила равносильны: 9, 11, (г), (д), (ж), (и), (к), (л), (м), (н), (о).
