4. Рекурсивно перечислимые отношения

Отношение P называется рекурсивным (РО), если рекурсивна характеристическая функция . Отношение P называется рекурсивно перечислимым (РПО), если существует такое рекурсивное отношение Q , что т.е. РП-мость отношения означает, что оно является проекцией РО по некоторой координате. Тогда проекция по нескольким координатам тоже РПО.

Предложение 1. Если Q -РО, , то отношение - РПО.

Предложение 2. Р,Q , R -РО, тогда отношения , , , , - рекурсивны.

Теорема Поста. Отношение P - рекурсивно P, - РПО.

Доказательство. Пусть P – рекурсивно, тогда , тогда по Пр.2. - РО, и P, - РПО.

Пусть P, - РПО. Т.е. и , где Q_1, Q₀

РО. Рассмотрим ЧРФ - она всюду определена, т.е. рекурсивна. Тогда , тогда P- рекурсивное отношение. 

4. Неразрешимость исчисления предикатов. Теорема Геделя о неполноте. Разрешимые и неразрешимые теории.

Далее докажем неразрешимость ИП арифметической сигнатуры

Исчисление I называется разрешимым, если существует алгоритм, позволяющий по любому выражению Ф узнать, доказуемо ли Ф или нет; в противном случае это неразрешимое исчисление.

Определение. Пусть W(A) – множество слов алфавита А. Геделевской нумерацией множества W(A) называется такая разнозначная функция , что существует алгоритм G, вычисляющий по слову w его номер g(w) и существует алгоритм , выписывающий по числу слово w, если n=g(w), и выдающий число 0, если .

Тогда в силу тезиса Черча вопрос о разрешимости исчисления, имеющего геделевскую нумерацию для каждого выражения исчисления, сводится к вопросу о рекурсивности множества геделевских номеров всех теорем исчисления.

Поэтому каждой формуле поставим геделевский номер , по которому можно эффективно распознавать структуру самой формулы.

Определение. Пусть и - множество термов и формул . Определим индукцией по числу шагов построения термов и формул геделевскую нумерацию по следующим правилам:

0)

1) , где v_n - n- я переменная из множества V.

2) , где

3) ,

4)

5)

6)

7) ,

8)

9)

10)

11)

12)

из ПР-ности c,l,r вытекает

Предложение 1.

1. Множество геделевских номеров термов 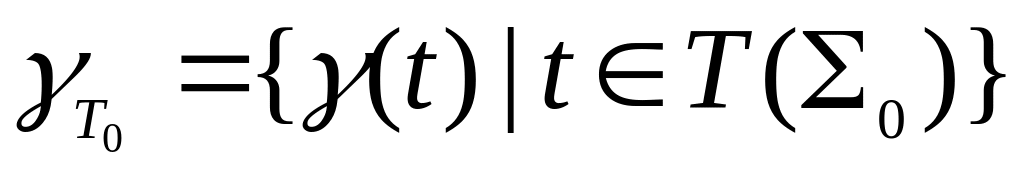- ПР-но.

2. Множество геделевских номеров формул 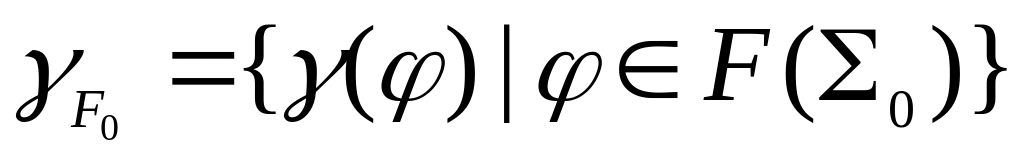- ПР-но

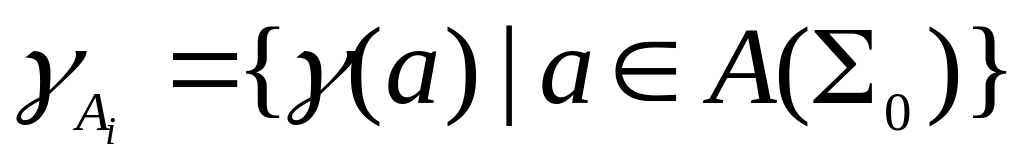
3. Множество геделевских номеров аксиом 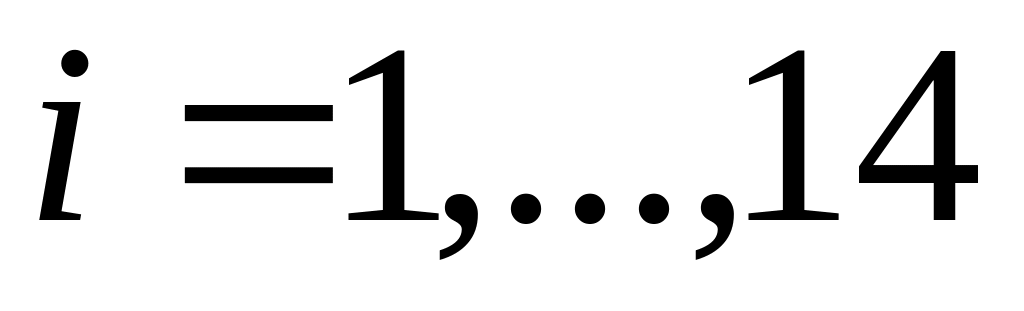- ПР-но

Для аксиом приведем пример примитивно-рекурсивного описания характеристической функции для множества A₁- геделевских номеров аксиомы :

Для 3-х правил вывода ИП также справедлива ПР-ность.

Пусть Sb(m,n,k) – функция, устанавливающая по геделевскому номеру m терма q и геделевскому номеру k терма t геделевский номер результата подстановки , а по геделевскому номеру m формулы , геделевскому номеру k терма t геделевский номер результата подстановки . Sb(m,n,k) – ПРФ.

Теорема 1. Множество геделевских номеров доказуемых формул , т.е. теорем, рекурсивно перечислимо.

Следствие. Если X- множество формул , у которого множество - рекурсивно перечислимо, то множество { }

Определение. Множество Г предложений сигнатуры Σ, замкнутое относи­тельно выводимости (т.е. содержащее все предложения, выводи­мые из Г в ИΠ^Σ), называется элементарной теорией или просто теорией сигнатуры Σ

Определение. Теорией 1-го порядка (или элементарной теорией или просто теорией) в называется любое дедуктивно замкнутое множество замкнутых формул (т.е. ).

Замкнутой формулой Σ или предложением называется формула Σ, не имеющая свободных переменных.

Mножество формул Σ T называется дедуктивно замкнутым, если для любой формулы из .

Множество замкнутых формул, которые выводимы в ИП из аксиом, называется формальной аксиоматической теорией (дедуктивной теорией)

Представим аксиомы , порождающие элементарную теорию арифметики:

1. 

2. 

3. 

4. 

5. 

6. 

7. 

8. 

9. 

Множество этих аксиом обозначим через

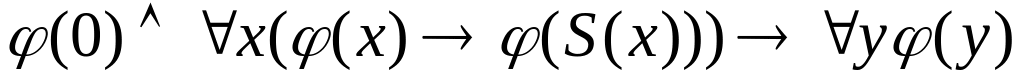10. - аксиома математической индукции.

10 аксиом составляют систему аксиом арифметики Пеано (обозначим P)

Определение. Функция назовем представимой в , если для некоторой формулы и любых чисел выполняются следующие условия:

• если 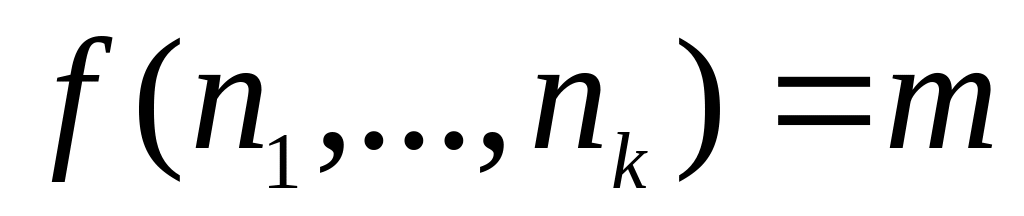, то

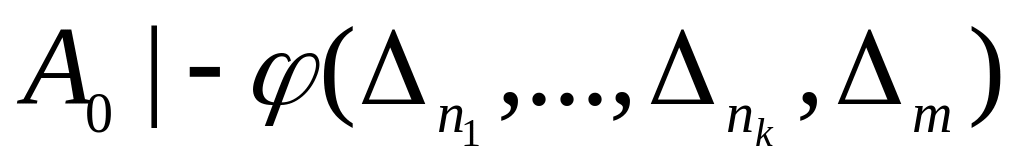
• если 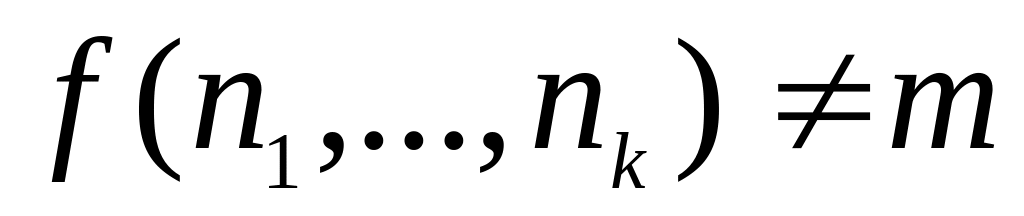, то

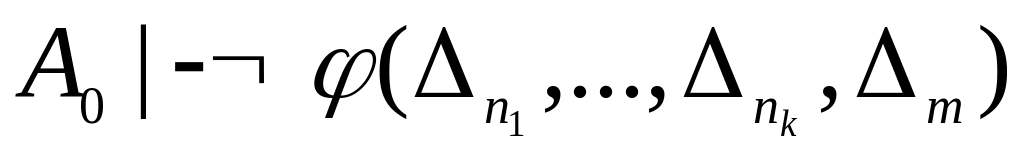
при этом формула называется представляющей для функции f.

Обозначим константу 0, через терм , .

Теорема 2. (о представимости) Любая рекурсивная функция представима в .

Теорема 3. Если X – непротиворечивое множество формул , содержащее множество , то множество нерекурсивно, где .

Доказательство. Рассмотрим термы и ПРФ Nm(n), определяемую схемой: Nm(0)=c(0,1), Nm(n+1)=c(2,Nm(n)), и задающую геделевские номера термов : Nm(n)= . Обозначим через Sb₀(x,y)=Sb(x,0,Nm(y))( ПРФ), где для любой формулы сигнатуры и любого справедливо . Предположим - рекурсивно, т.е. - рекурсивная функция. Рассмотрим формулу , не содержащую переменную v₀ и представляющую рекурсивную функцию . Положим . Если , то и следовательно . Однако в силу представимости в функции справедливо , а значит т.к. . Т.о. . Получили противоречие, т.к. Х – непротиворечиво по условии.

Пусть , тогда ; но в силу представимости в функции формулой , (т.к. ) и - противоречие. Т.о. -нерекурсивно. 

Определение. Непротиворечивая теория Т называется разрешимой, если множество геделевских номеров предложений из Т рекурсивно.

Следствие 1. (о неразрешимости теории элементарной арифметики) Для любого X – непротиворечивого множества формул , содержащего множество , теория Т_Х, порожденная множеством Х, неразрешима.

Т.е. не существует универсального алгоритма решения всех математических задач.

Следствие 2. (теорема Геделя о неполноте теории арифметики Пеано) Пусть X – непротиворечивое множество формул , содержащее множество , и - рекурсивно перечислимое отношение. Тогда теория Т_Х, порожденная множеством Х, неполна.

Доказательство. Предположим Т_Х – полно. Т.к. - РПО, то по Следствию Теоремы 1 -РПО. Но в силу полноты теории Т_Х, РП множество , поскольку оно состоит из всех натуральных чисел, не являющихся геделевскими номерами предложений , а также из геделевских номеров, предложений , для которых , тогда по теореме Поста -рекурсивно. Противоречие с теоремой 3.

Следствие 3. (теорема Черча о неразрешимости ) Множество геделевских номеров теорем исчисления нерекурсивно.

Доказательство. Пусть - конъюнкция формул из А₀.Очевидно, для любой формулы сигнатуры условие равносильно тому, что - теорема . Предположим, что множество - рекурсивно. Тогда рекурсивна функция . При этом f является характеристической функцией для множества Х геделевских номеров формул, выводимых из А₀. Это невозможно, т.к. по теореме 3 множество Х нерекурсивно. 

В силу теоремы Черча возникла задача нахождения разрешимых теорий. В частности, разрешимыми являются следующие теории:

• Th(<Q;< >),

• Th(<R;+,<,0,1, >),

• Th(<Q;+,-,0>),

• Th(<Z;+,-, 0>),

• Th(<N;+,S,0>)

• Th(<N; ,0>).

39