
Тема 5. Комплексные числа
Алгебраическая
![]()
Тригонометрическая
![]()
Форула эйлера\показательная:
![]() ,
,
Связь с тригонометрией:
![]()
![]()
Любые арифметические операции.
Брать корень и возводить в степень как и обычные числа.
Функции:
![]() ,
,
В квадратных уравнениях комплексное число может «выручить» дискриминант из отрицательности. Следовательно любое квадратное уравнение будет иметь 2 корня .
Теорема Абеля. Для n>5 нельзя выразить корни уравнения степени n через его коэффициенты при помощи радикалов.
Тема 6 Производная функции.
Производную
обозначают ![]() или
или ![]() .
.
из дифференцируемости функции следует ее непрерывность.
Пример y=|x|;
Тангенс угла наклона к касательной.
![]() , где х0 и
у0 – координаты точки. – касательная
, где х0 и
у0 – координаты точки. – касательная
![]() - нормаль
- нормаль
Производная пути , есть скорость. Итд.
![]() -
производная
простой ф-ции.
-
производная
простой ф-ции.
Для неявной запомнить , что производная от sin(y) является cos(y)*y’;
Для логарифмического нахождения – логарифмируем обе части.
Запомнить , что производная счиатется через деление y’(t) на x’(t)
Обратные – arcsin ; arcos ; arctg; arcctg; - таблица.
С гиперболическими – таблица.
ВФСА - это просто набор из нескольких обычных функций. Производной такой функции можно считать набор, состоящий из производных каждой функции в отдельности.
Механическая интерпритация - что нибудь из физики….
Если
кривая задана уравнениями в параметрической
форме ![]() ,
, ![]() и производные
и производные ![]() ,
, ![]() непрерывны
на отрезке [
непрерывны
на отрезке [![]() ,
, ![]() ]
, то длина дуги кривой выражается
интегралом
]
, то длина дуги кривой выражается
интегралом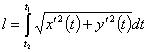 .где
и
—
значения параметра
.где
и
—
значения параметра ![]() ,
соответствующие концам дуги (
<
).
,
соответствующие концам дуги (
<
).
Тема 7. Дифференциал
Функция дифференцируема , если к этой функции можно провести провести касательную, хоть одну. Дифференциал – линейное приращение функции.
Применение
дифференциала в приближенных вычислениях
![]()
Правило нахождения дифференциала 1. Дифференциал постоянной величины dc=0.
2. Дифференциал сумм d(u+v)=du+dv.
3. Дифференциал произведения d(d·u)=du·v+dv·u.
4. Дифференциал
частного d![]() =
=![]() .
.
5. Дифференциал сложной функции y=f (u); u=f(x);dy=f ΄(u)·dxu.
Тема 8 Приложение теории дифференцирования
Правило Лапиталя – можно взять производные дроби(отдельно числитель, отдельно знаменатель) несколько раз, для нахождения предела. Тоже самое для замечательных переделов.
Теорема Ферма:
Для любого натурального числа n >2 уравнение
![]()
не имеет натуральных решений a, b и c.
Тема 9 Производные для графиков
Производные нужны для: Первая производная: нахождения экстремумов. И интервалы возрастания убывания. Вторая производная : точки перегиба, кривизна прямой. Вогнутость , выпуклость точка разрыва. Асимптоты находятся из самой функции, а не из производных.
Тема 10 . Неопределенный интеграл
Интеграл
от функции, это и есть нахождение его
первообразной. 1°.
Производная от н.и. равна подынтегральной
функции, а дифференциал — подынтегральному
выражению:![]()
![]()
2°.![]() в
частности,
в
частности,![]()
Свойства 1°, 2° следуют из определения н.и.
3°. Н.и. от алгебраической суммы конечного числа функций равен алгебраической сумме н.и. от каждого слагаемого.
Докажем,
что![]() (Равенство
понимается с точностью до постоянного
слагаемого.) Действительно, по 1°:
(Равенство
понимается с точностью до постоянного
слагаемого.) Действительно, по 1°:![]()
![]()
![]() Таким
образом,
Таким
образом,
левая и правая части имеют одинаковые производные и могут отличаться лишь постоянной
4°. Постоянный множитель можно выносить за знак н.и.:
![]()
5°.
Независимость вида н.и. от выбора
аргумента (инвариантность формы
интеграла):![]() где
где![]()
![]() имеет
непрерывную производную. Действительно,
по свойству инвариантности формы
дифференциала:
имеет
непрерывную производную. Действительно,
по свойству инвариантности формы
дифференциала:![]()
Частным
случаем 5° является![]() =
F(ax
+ b)
+ с.
=
F(ax
+ b)
+ с.
Очевидно, учитывая, что d(ax + b) = a dx, получаем формулу
![]()
Суть
замены состоит в том, что в функции
f(x+c)
и под знаком дифференциала d
, должно стоять одно и тоже выражение.
Если есть сумма или разность интегралов,
то можно применить интегрирование по
отдельности. Для
интегрирования рациональной функции ![]() ,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
,
где P(x) и Q(x) -
полиномы, используется следующая
последовательность шагов:
Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;
Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;
Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;
Вычислить интегралы от простейших дробей.
Определение. Универсальной тригонометрической подстановкой называются выражение тригонометрических функций через тангенс половинного аргумента.
sinx=2tgx2\1+tg2x2
 x
x =
=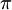 +2
n
n
+2
n
n Z;
Z;cosx=1+tg2x21\tg2x2 x = +2 n n Z;
tgx=2tgx21\tg2x2 x = +2 n n Z x =2
 +
n
n
Z;
+
n
n
Z;ctgx=2tgx2\1−tg2x2 x = n n Z x = +2 n n Z.
Для
интегрирования иррациональной функции,
содержащей ![]() используется
подстановка
используется
подстановка ![]() .
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x,
применяется подстановка в форме
,
где n полагается
равным наименьшему общему кратному
знаменателей всех дробных степеней,
входящих в данную функцию.
.
Чтобы
проинтегрировать иррациональную
функцию, содержащую несколько рациональных
степеней x,
применяется подстановка в форме
,
где n полагается
равным наименьшему общему кратному
знаменателей всех дробных степеней,
входящих в данную функцию.
