Матрица поворота в двумерном пространстве

В двумерном пространстве поворот можно описать одним углом со следующей матрицей линейного преобразования в декартовой системе координат:

Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:

.

Координаты (x',y') в результате поворота точки (x,y) имеют вид:

,

.

Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой стрелке в левосторонней системе координат.

[Править] Матрица поворота в трёхмерном пространстве

Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:

• Вращение вокруг оси x:

,

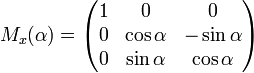• Вращение вокруг оси y:

,

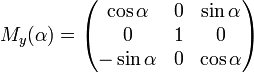• Вращение вокруг оси z:

.

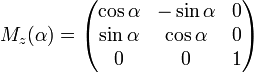Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть на плоскость вращении со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные. Правая система координат связана с выбором правого базиса (см. правило буравчика).

Свойства матрицы поворота.

Свойства матрицы поворота

Если  — матрица, задающая поворот вокруг оси на угол ϕ, то:

• 

• 

• 

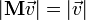
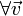
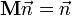
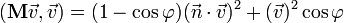
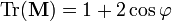• (след матрицы вращения)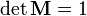

• (матрица имеет единичный определитель).

• если строки (или столбцы матрицы) рассматривать как координаты векторов , то верны следующие соотношения):

  • 

  • 

  • 

• Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о. .

24. Алгоритм Брезенхема для растеризации отрезка.

Алгоритм Брезенхе́ма (англ. Bresenham's line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.

Алгоритм

Отрезок проводится между двумя точками — (x₀,y₀) и (x₁,y₁), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x₁ − x₀ превосходит вертикальное y₁ − y₀, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x₀ и x₁, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y).

Общая формула линии между двумя точками:

Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:

Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y₀ и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона

которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.

Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:

function line(x0, x1, y0, y1)

int deltax := abs(x1 - x0)

int deltay := abs(y1 - y0)

real error := 0

real deltaerr := deltay / deltax

int y := y0

for x from x0 to x1

plot(x,y)

error := error + deltaerr

if error >= 0.5

y := y + 1

error := error - 1.0

Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:

function line(x0, x1, y0, y1)

int deltax := abs(x1 - x0)

int deltay := abs(y1 - y0)

int error := 0

int deltaerr := deltay

int y := y0

for x from x0 to x1

plot(x,y)

error := error + deltaerr

if 2 * error >= deltax

y := y + 1

error := error - deltax

Умножение на 2 для целых чисел реализуется битовым сдвигом влево.

Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца.