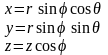Косоугольная система координат

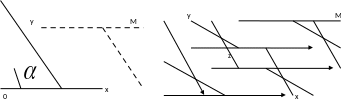
Декартова система координат	M(x,y,z)
Полярная	M( )
Цилиндрическая	M( )
Сферическая с коор.	M( )

0 в середине экрана у Картезианской системе координат.

(.) Все наши представления в векторах, в виде матрицы

Двумерная (2D — от англ. two dimensions — «два измерения») компьютерная графика классифицируется по типу представления графической информации, и следующими из него алгоритмами обработки изображений. Обычно компьютерную графику разделяют на векторную и растровую, хотя обособляют ещё и фрактальный тип представления изображений.

Трёхмерная графика (3D — от англ. three dimensions — «три измерения») оперирует с объектами в трёхмерном пространстве. Обычно результаты представляют собой плоскую картинку, проекцию. Трёхмерная компьютерная графика широко используется в кино, компьютерных играх.

Однородные координаты.

Однородные координаты

Определение. Однородные координаты — координаты, обладающие тем свойством, что определяемый ими объект не меняется при умножении всех координат на одно и то же число.

Однородными координатами вектора (х, у, z) является тройка чисел (x', y', z', w), где х = х' / w, у = y' / w, z = z' / w, а w — некоторое вещественное число (случай, когда w = 0 является особым).

Данные координаты не позволяют однозначно задать точку пространства. Например, (1, 1, 1, 1) и (2, 2, 2, 2) задают одну и ту же точку (1, 1, 1). При переходе к однородным координатам для точки с координатами (x, y, z) предлагается взять набор (x, y, z, 1). В процессе преобразований координата w может меняться. Обратный переход к декартовым координатам осуществляется посредством деления на w-координату.

ИЛИ

Однородные координаты - это математический механизм, связанный с определением положения точек в пространстве. Привычный аппарат декартовых координат, не подходит для решения некоторых важных задач в силу следующих соображений:

• В декартовых координатах невозможно описать бесконечно удаленную точку. А многие математические и геометрические концепции значительно упрощаются, если в них используется понятие бесконечности. Например, "бесконечно удаленный источник света".

• С точки зрения алгебраических операций, декартовы координаты не позволяют провести различия межу точками и векторами в пространстве. Действительно, (1,2,5) - это направление или точка?

• Невозможно использовать унифицированный механизм работы с матрицами для выражения преобразований точек. С помощью матриц 3x3 можно описать вращение и масштабирование, однако описать смещение (x=x+a) нельзя.

• Аналогично, декартовы координаты не позволяют использовать матричную запись для задания перспективного преобразования (проекции) точек.

Матрица переноса.

Перенос

Рассмотрим элементарные геометрические преобразования (двухмерные и трехмерные), применяемые в машинной графике. Эти преобразования основаны на матричных операциях.

Рассмотрим преобразования на плоскости - перенос, масштабирование, поворот.

Точку на плоскости можно перенести в новые позиции путем добавления к координатам этих точек констант переноса.

х' = х + Dx        у' = у + Dy

Определяем векторы строки

Р=[х,у]    Р'=[х',у']      T=[Dx,Dy]

Сдвиг точки в векторной форме

[x',y']=[x,y]+[Dx,Dy]

Или более кратко                           Р' =Р+Т

Объект можно перенести, применяя это выражение к каждой точке объекта. Однако для отрезка достаточно применить этот процесс только к его концевым точкам. Это справедливо и для масштабирования и для поворота.

Уравнение переноса

Пользуясь однородными координатами можно записать в виде однотипных матричных выражений все три вида преобразований.

|1 0 0 |

[x'y'1]=[x,y,1] |0 1 0 |

|Dx Dy 1 |

ил  Р' =Р ^. Т(Dx ,Dy )

Если перенести точку на (Dx1,Dy1), а затем на (Dx2,Dy2), то последовательным применением преобразования переноса суммарный перенос запишется в виде матрицы

| 1 0 0 |

| 0 1 0 |

|Dx1+Dx2 Dy1+Dy2 1 |

3-х мерный перенос

Трехмертные операции являются простым расширением двумерных.

T(Dx,Dy,Dz)

=

| 1 0 0 0 | | 0 1 0 0 | | 0 0 1 0 | | Dx Dy Dz 1 |

Свойства матрицы переноса.

Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.

23. Матрица масштабирования.

Масштабирование

Для масштабирования объекта каждую точку необходимо растянуть в S_x раз по оси х и в S_y раз по оси у.

х' = х ^. S_x        у' = у ^. S_y

Определяя

S=	| Sx 0 | | 0 Sy |

или P'=P ^. S

Отметим, что маштабирование производится относительно начала координат.

Масштабирование относительно других точек рассмотрим ниже.

Если S_x != S_y неоднородное масштабирование.

Если S_x = S_y однородное масштабирование.

Уравнение масштабирования

|S_x 0 0 |

[x'y'1]=[x,y,1]|0 S_y 0 |

|0 0 1 |

или P' = P ^. S(S_x ,S_y)

Последовательные масштабирования приводят к матрице

|S_x1S_x2 0 0 |

| 0 S_y1S_y2 0 |

| 0 0 1 |

Масштабирование

S(Sx,Sy,Sz)

=

| Sx 0 0 0 | | 0 Sy 0 0 | | 0 0 Sz 0 | | 0 0 0 1 |

Свойства матрицы масштабирования.

Умножение слева элементарной матрицы масштабирования на прямоугольную матрицу A приводит к умножению соответствующей строки матрицы A на число λ.

Умножение справа элементарной матрицы масштабирования на прямоугольную матрицу A приводит к умножению соответствующего столбца матрицы A на число λ.

Матрица поворота.

Поворот

Объект может быть повернут, ели координаты каждой его точки будут подвергнуты преобразованию

x' = х^.cosθ-y^.sinθ у' = х^.sinθ-y^.cosθ

В матричной форме

[x' у']=[x у]

| cosθ sinθ | | -sinθ cosθ |

или Р' = Р ^. R

Положительным считаются углы, измеряемые против движения часовой стрелки от X к Y.

В случае отрицательных углов можно воспользоваться тождествами

cos(-θ)= cos(θ) sin(-θ)=-sin(θ)

Поворот производится относительно начала координат

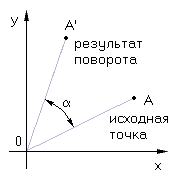
Однородные координаты

Преобразования переноса, масштабирования и поворота в матричной форме записываются как

P' = P + T P' = P ^. S P' = P ^. R

К сожалению, перенос в отличие от других реализуется с помощью сложения. Хотелось бы преобразования представить в такой форме, чтобы все эти элементарные преобразования можно было бы представить в одной форме - в виде произведений матриц. Тогда удастся совместить все три вида преобразований в виде умножения на одну результирующую матрицу геометрических преобразований.

Это можно сделать, представив точки в однородных координатах. Однородные координаты были введены в геометрии.

Точка Р(х,у) записывается как P(Wx,Wy,W) для любого масштабного множителя W не равного нулю. Переход от однородных к декартовым координатам x=X/W y=Y/W.

Уравнение поворота

| cosθ sinθ 0 |

[x'y'1]=[x,y,1]|-sinθ cosθ 0 |

| 0 0 1 |

или P' = P ^. R(θ)
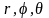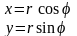
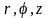