34.Затухающие колебания в колебательном контуре. Коэффициент затухания и логарифмический декремент затухания колебаний.

1. Колебательный контур.

Колебательный контур- это простейшая электрическая цепь, где можно наблюдать электромагнитные колебания, состоящая из конденсатора и катушки индуктивности, соединённых в замкнутую электрическую цепь. Колебательный контур применяется в качестве резонансной схемы во многих радиотехнических устройствах.

L

C

-

+ +

Дифференциальное уравнение свободных затухающих колебаний:

s- колеблющаяся величина, описывающая физический процесс. - коэффициент затухания в случае электромагнитных колебаний. -циклическая частота свободных незатухающих колебаний той же колебательной системы. - циклическая частота затухающих колебаний. -амплитуда затухающих колебаний.

Затухающие колебания принято характеризовать логарифмическим декрементом затухания:

, - амплитуда соответствующей величины(q,U или I). Логарифмическим декрементом затухания обратен числу колебаний , совершаемых за время , в течении которого амплитуда уменьшается в e раз: .

Частота , а следовательно, и определяются параметрами контура L, C, R. Таким образом , логарифмическим декрементом затухания является характеристикой контура. Если затухание не велико ( ), можно принять .Тогда

35.Вынужденные колебания в колебательном контуре . Резонанс.

Вынужденные электрические колебания.

Это незатухающие колебания заряда q, I, U в к.к. или электрической цепи, вызванные периодически изменяющейся ЭДС.

Переменный электрический ток представляет собой вынужденные электрические колебания, при которых сила тока изменяется по гармоническому закону с частотой, совпадающей с частотой вынуждающей ЭДС.

Если меняется с частотой , то I тоже будет изменяться с этой же частотой. Но фаза колебаний тока не обязательно совпадает с фазой U. Поэтому, если то . -сдвиг фаз между колебаниями тока напряжения. Зависит от !

I,U

I t

U

Электрический резонанс. Резонанс – явление резкого возрастания амплитуды вынужденных колебаний тела при совпадении частоты вынуждающей периодической силы с собственной частотой колебаний тела. При резонансе вынуждающая сила в течении всего периода колебания направлена в туже сторону, что и вектор скорости колеблющегося тела. Поэтому применяется закон Ома для участка цепи: .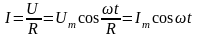

Резонансная частота:

Резонансная амплитуда:

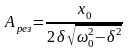
36. Работа и мощность переменного тока. Действующее значение тока и напряжения.

Найдем мощность, выделяемую в цепи переменного тока. Мгно­венное значение мощности равно произведению мгновенных значе­ний напряжения и силы тока:

* ** Воспользуемся формулой :

Выражению *** можно придать вид:

* *

Практический интерес представляет среднее по времени значе­ние Р(t), которое мы обозначим просто Р. Так как среднее значе­ние 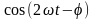равно нулю,

*

Из * *следует , что мгновенная мощность колеблется около среднего значения с частотой, в 2 раза превышающую частоту тока.

П одставив это значение 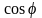в формулу * и учтя, что _{, получим}

Такую же мощность развивает постоянный ток, сила которого равна _{- действующее значение силы тока. - действующее значение напряжения.}

Выражение средней мощности через действующие значения силы тока и напряжения имеет вид

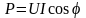
- коэффициент мощности. В технике стремятся сделать как можно больше. При малом для выделеия в цепи необходимой мощности нужно пропускать ток большей силы, что приводит к возрастанию потерь в подводящих проводах.