
4. Статистическая обработка эксперимента
4.1. Оценивание дисперсии эксперимента.
Определяются величины строчных дисперсий:
 ,
,
где m - кратность дублирования;
i - номер опыта;
j - номер j-го дубля в i-том опыте.
Результаты записываются в расширенную матрицу эксперимента.
4.2 Дисперсия эксперимента:
 ,
,
где N - число опытов в эксперименте.
4.3 Проверка постоянства дисперсии воспроизводимости.
При равномерном дублировании производится по критерию Кохрена:

где
 –
максимальная дисперсия в одном из
опытов;
–
максимальная дисперсия в одном из
опытов;
 –
табличное значение
критерия Кохрена;
–
табличное значение
критерия Кохрена;
f = m-1 – число степеней свободы этого критерия.
В данном случае:
 ,
,
где
 - критерий
Кохрена при
уровне значимости α = 5% [3].
- критерий
Кохрена при
уровне значимости α = 5% [3].
Следовательно, ряд дисперсий воспроизводим и первая предпосылка регрессионного анализа выполняется.
4.4 Абсолютная и относительная погрешности эксперимента
Абсолютная погрешность эксперимента находится как доверительная оценка истинного значения случайной величины при неизвестной точности измерений:%

где
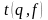 - значение критерия Стьюдента при
доверительно вероятности р = 0,95% и числе
степеней свободы
- значение критерия Стьюдента при
доверительно вероятности р = 0,95% и числе
степеней свободы
 .
Следует учитывать, что этот критерий
двухсторонний и поэтому α
= 0,5q,
где q
= 1-р.
По [3]
t(2,5;
16) = 2,1199. Поэтому:
.
Следует учитывать, что этот критерий
двухсторонний и поэтому α
= 0,5q,
где q
= 1-р.
По [3]
t(2,5;
16) = 2,1199. Поэтому:
 .
.
Относительная погрешность эксперимента равна:
 ,
,
где
 -
среднее значение отклика в эксперименте.
-
среднее значение отклика в эксперименте.
 ,
,
4.5. Оценка коэффициентов регрессии и свободного члена
Благодаря ортогональности плана ДФЭ оценивание коэффициентов регрессии существенно упрощается, т.к. нет необходимости решать систему нормальных уравнений МНК. Каждый коэффициент регрессии находится по своей формуле2
 ,
,
где
 –
номер опыта;
–
номер опыта;
 –
номера факторов (
–
номера факторов ( ).
).
 ,
,
В результате получается функция регрессии в кодированных значениях факторов:
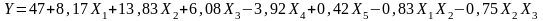 (3)
(3)
Проверка правильности вычислений подстановкой кодированных значений факторов из расширенной матрицы плана эксперимента п 1-й опыт:

что соответствует отклику первого опыта, равного 70.
4.6 Декодирование модели
Связь между кодированными Хi и натуральными значениями факторов xi
выражается соотношением:
 ,
,
где хi0 - нулевой уровень по таблице кодирования факторов;
Δi - интервал варьирования i - го фактора.
Раскрывая скобки и группируя члены, находим уравнение регрессии в натуральных значениях факторов:

4.6 Проверка значимости коэффициентов регрессии
Для отсеивания не значимых аi с некоторой вероятностью р используется t-критерий Стьюдента. Если

то
данный коэффициент регрессии значим.
Здесь
 ,
а
,
а
 –дисперсия
i-го
коэффициента регрессии. Дисперсия
оценивается
по формуле:
–дисперсия
i-го
коэффициента регрессии. Дисперсия
оценивается
по формуле:

где xij – j-е значение i-го фактора. Этот критерий является односторонним.
Дисперсии оценок коэффициентов регрессии (3):
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 .
.

Критерии Стьюдента для коэффициентов регрессии:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;

По [3] при f1 = 16 и α = 0,5 t16,5% = 1,7459. Т.о. все коэффициенты регрессии значимы. Следовательно, все введенные в эксперимент факторы являются существенно влияющими на отклик.
Расчетные значения отклика по (4):
у1 = 70 у2 = 26,667 у3 = 62,333 у4 = 53,333 у5 = 66,333 у6 = 21,667
у7 = 44,667 у8 = 31 у9 = 47.
Из сравнения с видно, что наибольшее расхождение с опытами плана имеется в 6-м опыте. Оно равно 0,33, т.е. относительное отклонение от экспериментального значения отклика составляет:

Но отклонение от отклика в центре плана больше: – 1,67. Поэтому тре-
буется проверка адекватности линейной модели.
4.7 Проверка адекватности линейной модели
При
выборе формы уравнения регрессии была
принята в качестве первого приближения
линейная зависимость. Теперь следует
проверить, насколько правильным было
это предположение. Проверка выполняется
сравнением дисперсии неадекватности
 с
дисперсией эксперимента. Следовательно,
нужно
с
дисперсией эксперимента. Следовательно,
нужно
проверить гипотезу:

Для проверки используется критерий Фишера:
 ,
,
где ν1– число степеней свободы дисперсии неадекватности
ν1 = mN – (d+1);
ν2 – число степеней свободы дисперсии эксперимента
ν2 = N(m – 1).
Этот критерий является односторонним.
При равномерном дублировании опытов
 ,
,
где
 –
расчетное по уравнению регрессии
значение отклика в і-том
опыте.
–
расчетное по уравнению регрессии
значение отклика в і-том
опыте.
d - число значимых коэффициентов регрессии.
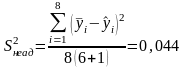 .
.
 ,
,
где
величина
 найдена по таблицам [3]. Очевидно, что
линейная аппроксимация адекватна.
найдена по таблицам [3]. Очевидно, что
линейная аппроксимация адекватна.
4.8 Определение точности регрессионной модели
Производится так же, как и точности эксперимента, но вместо дисперсии эксперимента используется дисперсия неадекватности.
Абсолютная погрешность определения отклика по регрессионной модели:

где
 - значение критерия Стьюдента при уровне
значимости α и числе степеней свободы
при равномерном дублировании
- значение критерия Стьюдента при уровне
значимости α и числе степеней свободы
при равномерном дублировании
 .
.
Следует учитывать, что этот критерий двухсторонний и поэтому α = 0,5q, где q = 1– р.
 ,
,
где
 = 1,655 [3].
= 1,655 [3].

Относительная погрешность определения отклика по регрессионной модели равна:
 ,
,
где
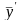 =
среднее значение отклика по регрессионной
модели.
=
среднее значение отклика по регрессионной
модели.
Видно, что точность регрессионной модели практически не отличается от точности эксперимента. Данное снижение точности объясняется дополнительными погрешностями аппроксимации. Следовательно, адекватность линейной модели подтверждена.
