2. Оценки математического ожидания и дисперсии. Выборочное среднее как несмещенная, состоятельная оценка математического ожидания. Выборочная и исправленная выборочная дисперсия.

В качестве статистической оценки математического ожидания принимают выборочное среднее. В качестве статистической оценки дисперсии D(X) случайной величины X примем выборочную дисперсию.

Выборочным среднем называется среднее арифметическое элементов выборки

(1.4)

Покажем, что выборочное среднее является несмещенной и состоятельной оценкой. Для этого предварительно заметим, что в теоретических рассуждениях выборку x1, x2, ... , х_n обычно рассмат­ривают как некоторую реализацию случайного вектора с n независи­мыми компонентами X1, Х2, ... , х_n , каждая из которых имеет распре­деление генеральной совокупности с теми же числовыми характери­стиками.

С учетом этого замечания установим несмещенность .

M( )=M((l/n) )=M((l/n) )=(l/n)*n*M(X)=M(X).

Состоятельность выборочной средней х как оценки М(Х) следует из закона больших чисел (теорема_Чебышева )[2, 3, 7].

По поводу эффективности заметим, что если случайная вели­чина X распределена по нормальному закону, то выборочное среднее является эффективной оценкой математического ожидания.

Выборочной дисперсией называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выбороч­ного среднего

S² = (l/n) (_Xi- )². (1.5)Можно показать, что оценка S² является смещенной. Для полу­чения несмещенной оценки дисперсии выборочную дисперсию S исправляют, умножая ее на множитель n/(n-1). Исправленная дис­персия

So² =(n/(n-l))S²=(l/(n-l)) (_Xi -x)² (1.6 )является уже несмещенной оценкой дисперсии. Оценка S² (а вместе с ней и S₀²) состоятельна.

3. Точность и надежность оценки. Доверительный интервал. Доверительные интервалы для оценки математического ожидания и среднеквадратического отклонения нормального распределения.

Для выборок небольшого объема вопрос точности оценок решается с помощью интервальных оценок. При этом по вычисленной точечной оценке а* параметра а при заданной вероятности γ и а*, строят интервал для истинного параметра а: а*- ε<a<а*+ ε, чтобы выполнялось равенство: P(а*- ε<a<а*+ ε)=γ. Число ε называется точностью оценки а*, границы интервала а*- ε и а*+ ε называются доверительными границами, интервал (а*- ε;а*+ ε) – доверительным интервалом, вероятность γ – доверительной вероятностью или надежностью интервальной оценки.

Интервальной оценкой математического ожидания m нормального распределения при известной дисперсии σ² называется интервал , удовлетворяющий равенству: , где – заданная доверительная вероятность, m – истинное математического ожидание, – точечная оценка математического ожидания, n – объем выборки; число находится из уравнения с помощью табл.2 функции Лапласа Ф(х).

Следовательно, интервальная оценка математического ожидания находится по формуле:

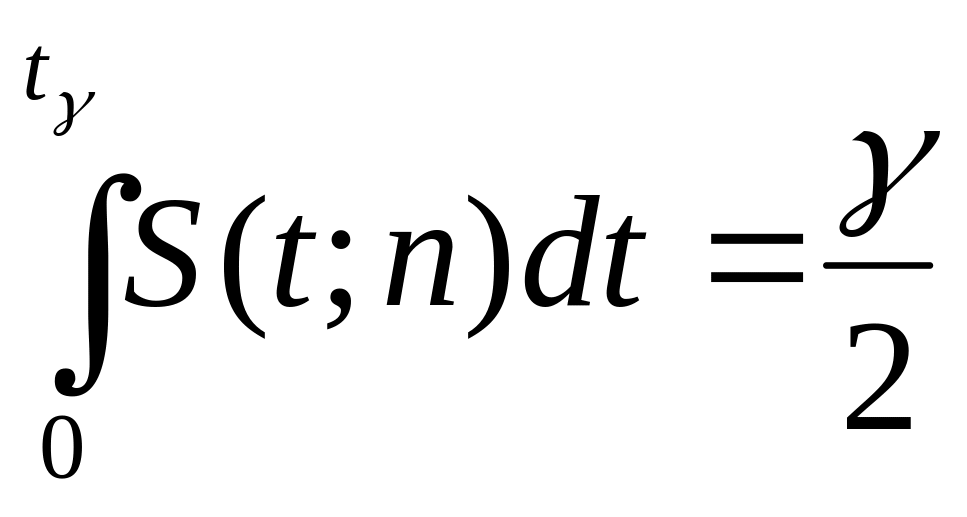Интервальной оценкой математического ожидания m нормального распределения при неизвестной дисперсии называется интервал , удовлетворяющий равенству: где – заданная доверительная вероятность, m – истинное математическое ожидание, – точечная оценка математического ожидания, s² – точечная оценка дисперсии, n – объем выборки, число вычисляется из уравнения с помощью таблицы распределения Стьюдента. Следовательно, интервальная оценка математического ожидания с доверительной вероятностью вычисляется по формуле: .

Интервальной оценкой среднего квадратического отклонения σ нормального распределения называется интервал: удовлетворяющий равенству где – заданная доверительная вероятность, s² – исправленная выборочная дисперсия, n – объем выборки, число определяется ил таблицы4.

Следовательно, интервальная оценка среднего квадратического отклонения находится по формулам: если , если .

4. Статистическая проверка гипотез. Виды гипотез. Ошибки первого и второго рода. Статистические критерии проверки нулевой гипотезы. Критическая область. Проверка гипотез для нормального распределения. Корреляционная зависимость. Нахождение параметров уравнения линейной регрессии методом наименьших квадратов. Выборочный коэффициент корреляции, его свойства.

Статистической гипотезой называется предположение о виде распределения, о параметрах известных распределений. Например, стат.являются гипотезы: 1) генеральная сов-ть распределена по закону Пуассона( здесь сделано предложение о виде неизвестного распределения); 2) дисперсия двух нормальных сов-тей равны между собой (о параметрах двух известных гипотез)

Выдвинутая гипотеза называется нулевой (или основной) и обозначается Н_о.

Гипотеза, которая противоречит нулевой, называется конкурирующей гипотезой (или альтернативной гипотезой) и обозначается Н₁.

Гипотеза называется простой, если она содержит только одно предположение.

Гипотеза называется сложной, если она состоит из конечного или бесконечного числа предположений.

Ошибкой первого рода называется решение отвергнуть нулевую гипотезу H_o и принять конкурирующую гипотезу Н₁, если на самом деле гипотеза Н_о верна. Вероятность ошибки первого рода равна уровню значимости α.

Ошибкой второго рода называется решение принять нулевую гипотезу Н_о, то есть отвергнуть конкурирующую гипотезу Н₁, если на самом деле гипотеза Н₁ верна.

Гипотеза Н₀ проверяется с помощью статистического критерия.

Статистическим критерием (критерием) называют однознач­но определенное правило, устанавливающее условия, при которых проверяемую гипотезу Но следует или отвергнуть, или принять. В ос­нове критерия- функция Т= Т( х1, ..., хn) от выборочных данных (т. е. статистика критерия ), распределение которой известно. Примера­ми таких распределений, на основе которых построено большинство критериев, являются: нормальное, х2(хи-квадрат) - распределение, распределения Стьюдента и Фишера.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотез (об допустимых значений) называют совокупность значений критерия, при кот гипотезу принимают. Критическими называются точки, отделяющие критические области от областей принятия гипотез.

Различают правостороннюю, левостороннюю, двустороннюю критические области Правосторонней критической областью для проверки нулевой гипотезы с уровнем значимости α называется совокупность значений критерия проверки Z, для которых выполняется равенство: P(Z>Z_крит)= α. При этом Z_крит называется границей критической области.

.

Правосторонняя критическая область определяется неравенством: Z> Z_крит.

Левосторонняя критическая область определяется неравенством: Z<- Z_крит.

Односторонней называют правостороннюю или левостороннюю критическую облась.

Двусторонняя критическая область определяется неравенствами Z> Z_1крит и Z> Z_2крит.

Проверка гипотезы о нормальном распределении генеральной совокупности. Критерия согласия Пирсона.

Критерием согласия называется критерий проверки гипотезы о предлагаемом законе распределения.

Критерий согласия Пирсона (критерий проверки гипотезы о нормальном распределении генеральной совокупности):

1) По выборке объема n построить статический ряд:

2) Вычислить по таблице оценку математического ожидания и выборочное среднее квадратическое ожидание σ_в.

3) В предположении нормального распределения генеральной совокупности вычислить теоретические частоты m_{1 теор},…,m_{l теор} по формуле: m_{i теор.}=np_i, где , Ф(х) – интегральная функция распределения Лапласа.

4) Вычислить число по формуле: или

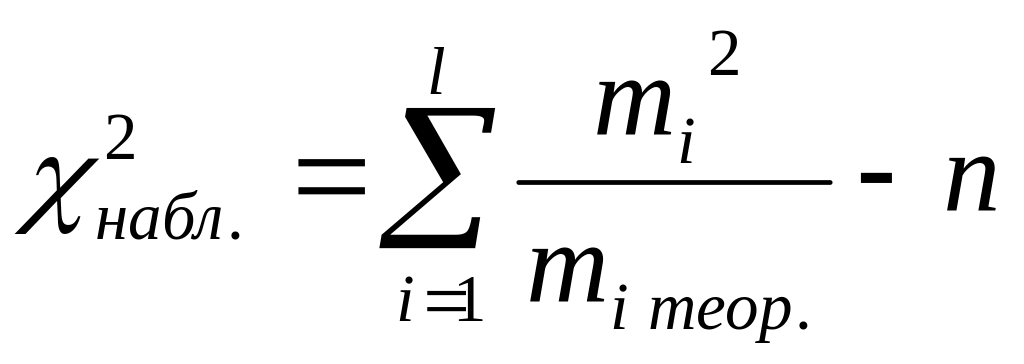
5) По табл. 5 приложения найти число , учитывая заданный уровень значимости α и число степеней свободы k=l-3.

6) Сравнить число и :

• если < , то нет основания отвергать гипотезу о нормальном распределении генеральной совокупности;

• если > , то гипотезу о нормальном распределении генеральной совокупности следует отвергнуть.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распреде­ления другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае ста­тистическую зависимость называют корреляционной.

Корреляция в математической статистике, вероятностная или статистическая зависимость, не имеющая, вообще говоря, строго функционального характера. В отличие от функциональной, корреляционная зависимость возникает тогда, когда один из признаков зависит не только от данного второго, но и от ряда случайных факторов или же когда среди условий, от которых зависят и тот и другой признаки, имеются общие для них обоих условия.

Метод наименьших квадратов применяется для нахождения оценок неиз­вестных параметров функциональной зависимости y=f{x), вид которой пред­полагается известным. Пусть на опыте получено k пар результатов измерений (х_i, уi), где i=l, 2,..., k. Предположим, что зависимость между X и Y близка к линейной. В этом случае естественно искать зависимость у=ах+b.

Рассмотрим оценку по методу наименьших квадратов парамет­ров а и b.Из условия минимума суммы

эти оценки вычисляют по формулам:

(4.5)

(4.6)

Если предположить, что независимы, М( )=0, D( )= и полагая , можно показать, что оценки параметров а и b линейной регрессии, полученные методом наименьших квадратов, определяют по формулам:

Из этих равенств следует, что

Таким образом, оценки а*,b* являются несмещенными оценками параметров а и b. Оценки а* и b* состоятельны, если при k ->оо, так как в этом случае D(a*)-»0, D(b*)-»0.

Выборочный коэффициент корреляции r

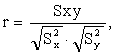где ,

Выборочный коэффициент корреляции r является оценкой коэффициента корреляции генеральной совокупности и поэтому служит для измерения линейной связи между величинами – количественными признаками Y и X.

r имеет свойства 1,3 коэффициента r, что позволяет использовать его как меру линейной связи между х и у:

1)

3) r = 1 тогда и только тогда, когда между x и y существует линейная зависимость.

В самом деле, если r = 1, то дискриминант трехчлена f(a) равен нулю, и существует единственный корень уравнения f(a) = 0, обозначим его ао. Тогда , выражение под знаком математического ожидания равно нулю, то есть или .

Обратно, если y линейно выражается через x:

СЛУЧАЙНЫЕ ПРОЦЕССЫ.

Случайной функцией называют функцию неслу­чайного аргумента t, которая при каждом фиксированном значении аргумента является случайной величиной. Слу­чайные функции аргумента t обозначают прописными буквами X (t), Y (t) и т. д.

Например, если U—случайная величина, то функция Х(t) =t²U — случайная.

I Случайным (стохастическим) процессом называют слу­чайную функцию аргумента t, который истолковывается как время. Например, если самолет должен лететь с за­данной постоянной скоростью, то в действительности вследствие воздействия случайных факторов (колебание температуры, изменение силы ветра и др.), учесть влияние которых заранее нельзя, скорость изменяется. В этом примере скорость самолета – случайная функция от непрерывно изменяющегося аргумента (времени), те скорость есть случайный процесс.

Важнейшим классом случайных процессов, встречающихся на практике,

является класс стационарных случайных процессов. Случайный процесс

называется стационарным в узком смысле, если его многомерная функция

распределения (и, следовательно, числовые характеристики) не зависит от

начала отсчета времени, т.е. от сдвига всех сечений вправо или влево на

один и тот же интервал времени t.

Иногда случайный процесс называют стационарным в широком смысле,

если приведенные условия выполняются лишь для числовых характеристик.

Узкое и широкое определения стационарности не тождественны. Случайные

процессы, стационарные в узком смысле, всегда стационарны в широком

смысле, но не наоборот.

Случайный процесс называется марковским, если для любого момента времени t0 вероятностные характеристики процесса в будущем зависят только от его состояния в данный момент t0 и не зависят от того, когда и как система пришла в это состояние.

13