9.Формула полной вероятности. Формулы Байеса.

Теорема (формула полной вероятности). Вероятность события А, которое может наступить лишь при условии наступления одного из попарно несовместных событий Н1,Н2,…,Нn, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А:

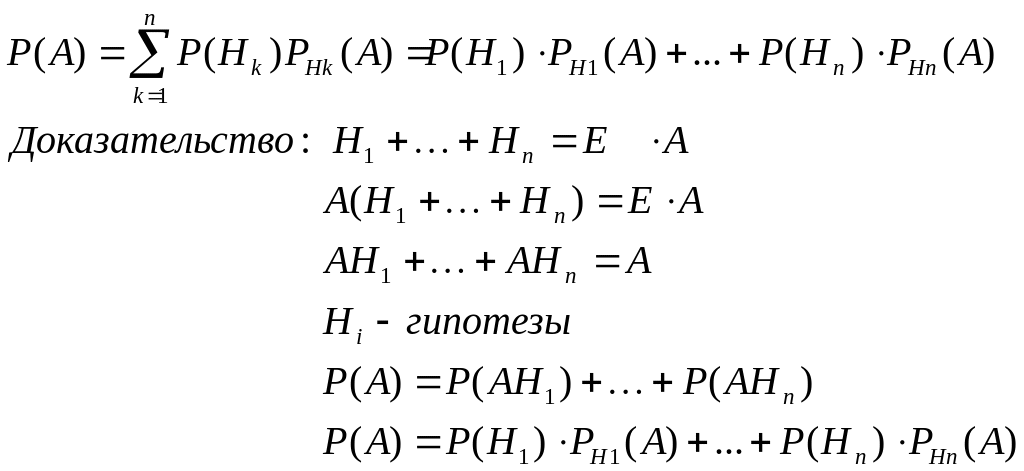Появление события А изменит вероятности элементарных событий. Причем вероятность осуществления события после наступления события А определяется следующей формулой Бейеса:

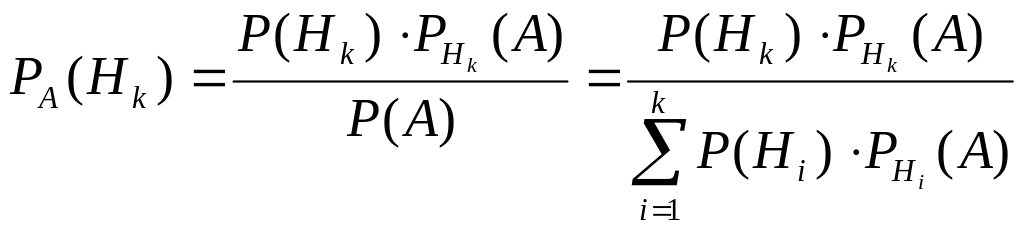
10. Схема Бернулли.

Под схемой Бернулли понимают конечную серию повторных независимых испытаний с двумя исходами. Вероятность появления (удачи) одного исхода при одном испытании обозначают , а непоявления (неудачи) его . Я. Бернулли установил, что вероятность ровно успехов в серии из повторных независимых испытаний вычисляется по следующей формуле:

То значение , при котором число является максимальным из множества { }, называется наивероятнейшим, и оно удовлетворяет условию

np - q m np+ p,

Формулу Бернулли можно обобщить на случай, когда при каждом испытании происходит одно и только одно из событий с вероятностью ( . Вероятность появления раз первого события и - второго и -го находится по формуле

При достаточно большой серии испытаний формула Бернулли становится трудно применимой, и в этих случаях используют приближенные формулы. Одну из них можно получить из предельной теоремы Пуассона:

Формула Бернулли.

Теорема (формула Бернулли). Пусть в серии n одинаковых независимых испытаний в каждом испытании может наступить либо событие А с вероятностью р, либо событие с вероятностью q=1-p. Тогда вероятность P_n(m) того, что в этой серии испытаний событие А наступит ровно m раз, вычисляется по формуле Бернулли: , где .

11.Случайные величины: дискретные, непрерывные. Закон распределения дискретной случайной величины. Многоугольник распределения.

Случайной называется величина, принимающая в результате испытания только одно значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.

Различают два типа случайных величин: дискретные и непрерывные.

Случайная величина Х называется дискретной, если в результате испытания она принимает одно из конечного или бесконечного множества значений х₁,х₂,….

Случайная величина Х называется непрерывной, если множество ее значений заполняет полностью некоторый промежуток (a;b).

Законом распределения вероятностей дискретной случайной величины называется зависимость между возможными значениями x_k (k=1,2,…) дискретной случайной величины и их вероятностями p_k (k=1,2,…).

Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, когда в прямоугольной системе координат строят ломанную, соединяющую последовательно точки координатами (x_k; p_k), k=1,2,…. Полученную линию называются многоугольником распределения.

Функция распределения случайной величины, ее свойства.

Функцией распределения (или интегральной функцией распределения) случайной величины Х называется функция F(x), равная при каждом вероятности того, что Х в результате испытания примет значение, меньшее х: F(x)=P(X<x), .

Свойства:

1)

2) F(x) – неубывающая функция.

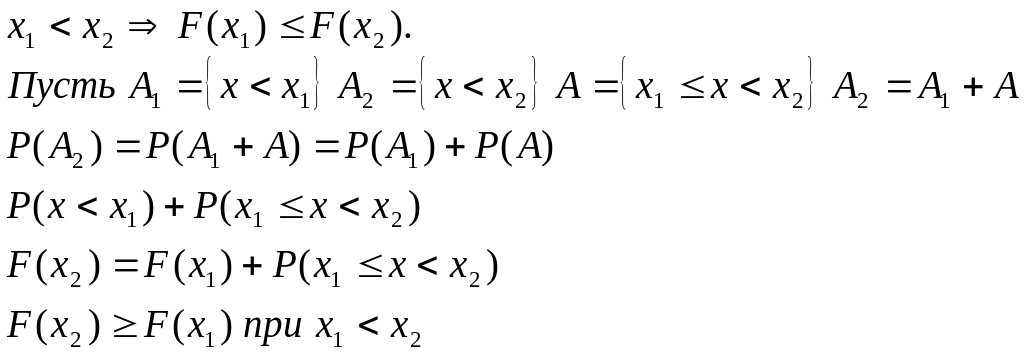
3) F(x) – непрерывны слева ;

4) ;

5) вероятность того, что непрерывная случайная величина Х примет одно определенное значение, равна 0;

6) если Х – непрерывная случайная величина, то функция F(x) непрерывна на .

Плотность распределения непрерывной величины, ее свойства.

Плотностью распределения вероятностей (или дифференциальной функцией распределения) непрерывной случайной величины Х называется функция f(x), задаваемая равенством f(x)=F’(x), .

График функции f(x) называется кривой распределения величины Х.

Свойства:

1) ;

2) ;

3) Теорема о вероятности попадания в заданный интервал.

Х – непрерывная случайная величина, f(x) – плотность распределения,

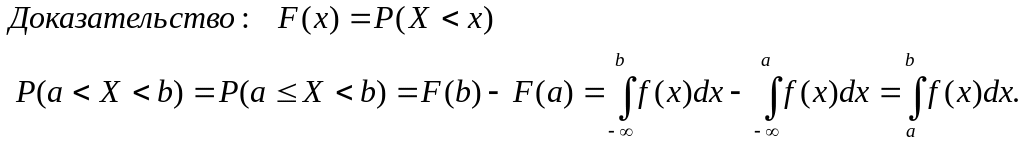
4) условие нормировки;

5) геометрически вероятность попадания случайной величины Х в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми x=a, x=b.

6) Если все значения случайной величины Х заключены в промежутке (a₁;a₂), то

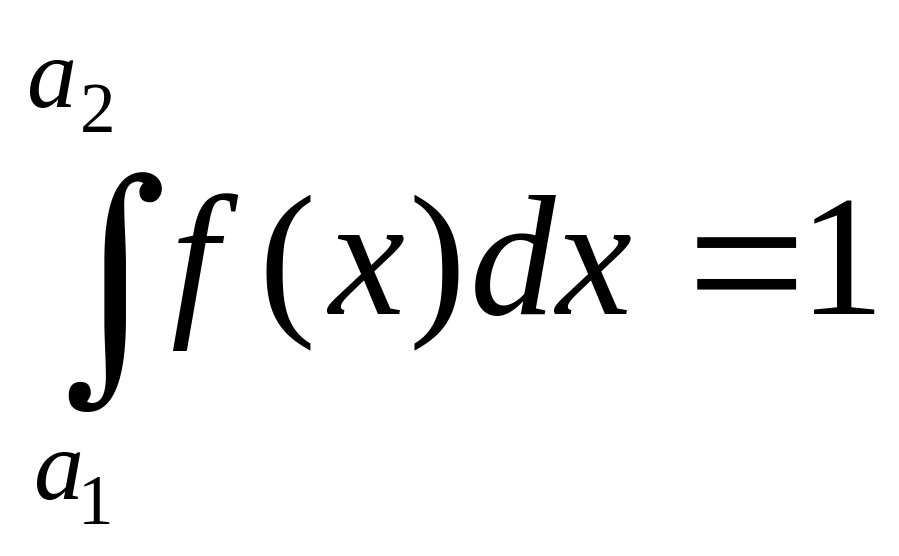
12. Пусть имеется случайная величина Х с математическим ожиданием mx.

Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания. Центрирование случайной величины равносильно переносу начала координат в точку, абсцисса которой равна математическому ожиданию.

Мат ожид приближенно = среднему знач случ величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.

M(Х)=интеграл от i=1 до бескон хipi

Если дискретная случайная величина X принимает счетное множество возможных значений, то математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,Ь], называют определенный интеграл

ь М(Х)=интегрxf(x)dx

а

Если возможные значения принадлежат всей оси Ох, то

M(X)=интегр от – беск до +беск xf (x)dx.

Предполагается, что несобственный интеграл сходится абсолютноСвойства математического ожидания.

1. Математическое ожидание постоянной величины равно самой постоянной.

М(С) = С.

2. Постоянный множитель можно выносить за знак математического ожидания. М(СХ)=СМ(Х).

3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий.

X xi x₂ Y yi у₂

Р Pi Рг g gi g₂

Составим все значения, которые может принимать случайная величина XY

XY xiy, х,у₂ x₂yi х₂у₂

^Р Plgl Plg2 P2gl P2g2

Математическое ожидание равно сумме произведений всех возможных

значений на их вероятности:

M(XY) = Xiyip^i + x₂yip₂qi + X!y₂piq₂ + х₂у₂р_2Ч2 = - yi4i(xiPi + х₂р₂) + УгчгСхф! + хгр₂) = (x,pi + x₂p₂)(yiq, + y₂q₂) = = M(X) + M(Y).

Мат ожид суммы двух случ величин = сумме мат ожид слагаемых. М(Х+Y)=М(Х)+М(Y)