30 Ряд Лорана.

Ряд Лорана

Н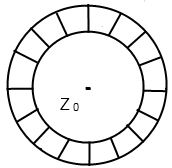 ехай f(z) – аналітична в кільці:

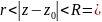
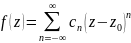- цей ряд наз. Рядом Лорана

Ряд Лорана має дві частини:

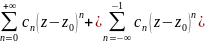
Правильна головна

Коефіціенти знаходяться за формулами:

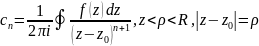
Доведення: розглянемо кільце, яке лежить всередині нашого кільця:

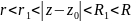
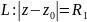
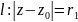
Розглянемо довільну точку Z всередині кільця:

За узагальненою теоремою Коші:

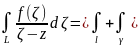
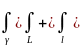
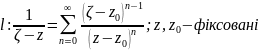
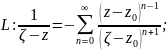
Підставимо ці ряди в інтеграли. Проінтегруємо почленно і за інтегрально формулою Коші:

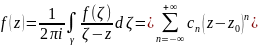
31 Особливі точки фкз. Їх класифікація.Ряд Лорана в усувн.Т.

Особливі точки аналітичної ф-ї:

z₀ – називається ізольованою особливою точкою аналітичної ф-ї f(z), якщо в точці z₀ вона не є аналітичною, але існує окіл в кожній точці якого f(z) – аналітична.

Класифікація особливих точок:

1)Усувний

.

.

.

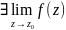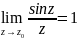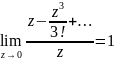2)Полюс

.

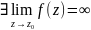f(z)=1/z; z₀ =0 – полюс

3)Істотно-особлива:

.

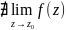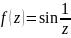, z₀=0 – істотно-особлива.

4)Полюс має порядок.

Кажуть, що z₀ – полюс порядка n, якщо = ;

;

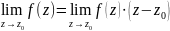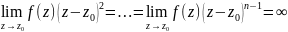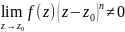Характер особливої точки залежить від вигляду ряда Лорана ф-ї f(z) в околі точки z₀.

Теорема: якщо z₀ – усувна, то ряд Лорана має вигляд f(z)=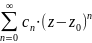

Дов-ня: покажемо, що коефіцієнти : с_-1=с_-2=…=0

.

Нехай γ – це коло радіуса r:

|z-z₀|=r

Оскільки існує limf(z)⇒|f(z)|<M

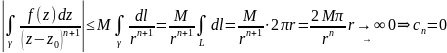, n<0 ▲

32 Ряд Лорана в полюсі.

Ряд Лорана в полюсі:

Теорема: якщо z₀ –полюс порядку N, тоді ряд Лорана f(z)=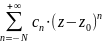 (ряд Лорана скінченну кількість степенів).

Дов-ня: оскільки

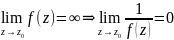
Отже, ф-я φ(z)=1/f(z); z₀ – усувна.

Розкладемо φ(z) в ряд Лорана:

φ(z)= …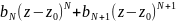

b_N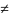 0, N>0

Тоді,

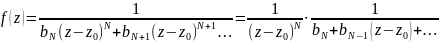
Другий множник є ф-я аналітична в точці . За попередньою теоремою:

.

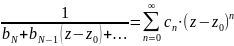f(z)= ▲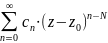

Зауваження: N–це порядок полюса,тому що

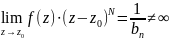
33 Лишки, їх обчислення. Обчислення лишків в полюсі. Лишки

Якщо z₀ – особлива точка ф-ції f(z₀), толишок f(z) в точці z₀ – це число, яке позначається Res(f(z);z₀)≡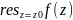 = 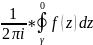, де γ-коло з центром в z₀.

Очевидно, що коли f(z) – аналітична в точці z₀,то її лишок в цій точці =0.

Теорема Коші

Якщо функція f(z) є аналітичною в замкненій області D, обмежена контуром L, за винятком скінченного числа особливих точок z_k(k=1,2,3…), що лежать в середині області D, то

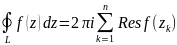
Дов-ня

Н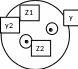 авколо кожної особливої точки 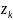опишемо кого так, щоб вона повністю містилась в області D, не містила всередині інших особливих точок і щоб ніякі з цих кіл не мали спільних точок.

Тоді за теоремою Коші для багато зв’язної області маємо:

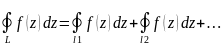
Де при інтегруванні всі контури обходяться проти годинникової стрілки

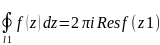
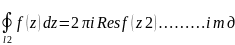
Відповідно

▲

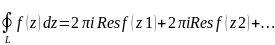
Обчилення лишків

1)Усувна res(f(z))=0

2) Полюс

А) порядок N=1

Представимо 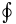у вигляді ряду Лорана:

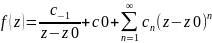
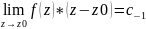
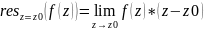
Б) N>1 (порядок полюса)

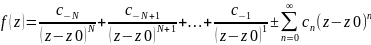
Помножимо рівність на

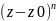
Продиференціюєм N-1 раз, отримаємо:

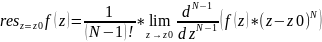
34 Перетв Лапласа.Зображення деяких оригіналів

Означення:

Функція дійсної змінної f(t), t є R називається оригіналом, якщо:

1)f(t)=0 при t<0

2) f(t)- кусково-неперервна разом зі своїми похідними

3) Ǝ М>0, S>0 такі, що для будь-якого t:

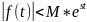
Інтегральне перетворення вигляду: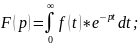 p є C називається перетворенням Лапласа

Теорема:

Для кожного оригіналу f(t) зображення 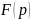існує в півплощині Re(p)=s>s0, де s0 – показник росту функції f(t), причому функція являється аналітичною в цій півплощині (s>s0)