26 Інтегральна теорема Коші. Узаг. Теорема коші.

Теорема коші Якщо функція f(z) аналітична в однозвязнів області D то інтеграл від цієї функції по будьякому замкненому контуру L що лежить в області D дорывнюэ нулю тобто Доведемо теорему припускаючи неперервність похідної 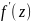Оскільки відом що . В силу аналітичності і неперервності воднозвязній області D, функції u=u(x;y) v=v(x;y) неперервні і диференційовні в цій одбалті і задовольняють умовам Ейлера-Даламбера; і Ці умови означають рівність нулю інтегралів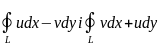 . Відповідно . Наслідок Якщо f(z) аналітична функція в однозвязній області D то інтеграл від неї не залежить від форми шляху інтегрування, а залежить лише від початкової і кінцевої точок інтегрування.

F(z) первісна f(z) в області D якщо

невизначений інтеграл

Інтеграл Коші Інтегральна, формула Коші

Нехай функція f(z) аналітична в замкнутій однозвязній області і L Тоді має місце формула де z0 Є D- будьяка точка в області D, а інегрування по контуру L виконується в додатньму напрямку( проти годинникової стрілки)

Теорема(Наслідок) Для будьякої диференційовної в точці z0 функції f(z) існують похідні всіхпорядків, причому n-на похідна має вигляд

27 Інтегр. Ф-ла Коші

Т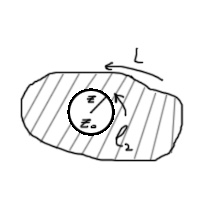 еорема: Нехай f(z)-аналітична в однозв’язній області z. -замкнена жорданова крива, яка належить разом із своєю внутрішньою частиною, точка -лежить всередині . Тоді f( dz.

Доведення: Заштрихована область ­­– двохзв’язна область , обмежена контурами , в якій функція – аналітична. Тоді, згідно наслідку до теор. Коші, маємо:

. Звіси слідує:

Але Звідси:

Оцінимо різницю в лівій частині рівності (1). Так як аналітична функція неперервна в точці є D, то для будь-якого числа знайдеться число таке, що при

(на колі маємо ) справедлива нерівність:

Отже маємо:

Так як можна вибрати як завгодно малим, а ліва частина останньої нерівності не залежить від то вона рівна нулю:

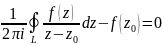
28 Первісна функції комплексної змінної(довести самост.)

Теорема: Якщо – аналітична в однозв’язній області, то функція: – аналіт. І .

Доводення:

Функція

Можна показати, що якщо , де С=const. Сукупність всіх первісних функцій називається невизначеним інтегралом від функції і позначається ,

Нехай функція є первісна функції для . Звідси, = . Підставим тут z=z0, отримаємо:

0= (контур замикається, інтеграл дорівнює нулю). Звідси, С= - , а значить:

=

Отримана формула називається формулою Ньютона- Лейбница.

29 Ряд Тейлора(фкз). Формула Коші для похідної.

Теорема: – аналітична ф-ія. Область збіжності цього ряду – круг:

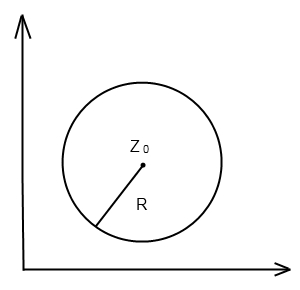Теорема: якщо - аналітична в області : , то ії можна представити у вигляді:

. Цей ряд – ряд Тейлора, бо

Доведення: Запишемо інтегральну формулу Коші:

Розкладемо в степеневий ряд ф-цію, користуючись формулою неск. Складної геометричної прогресії:

П ідставимо цей ряд в інтеграл та про інтегруємо його почленно. Одержимо:

Наслідок: Якщо порівняти коефіцієнти з різних формул, одержимо формулу Коші для похідної: