
- •1 Ряди. Властивості збіжних рядів.
- •В ластивості збіжних рядів
- •2 Теореми порівняння
- •3 Ознаки збіжності числових рядів з додатними членами
- •4 Знакозмінні ряди. Ознака Лейбніца. Абсолютно і умовно збіжні ряди, їх властивості.
- •5 Функціональні ряди. Властивості рівномірно збіжних рядів
- •6 Неперервність суми функціонального ряду
- •7 Почленне інтегрування та диференціювання раціональних рівнянь
- •8 Степеневі ряди. Теорема Абеля. Радіус збіжності.
- •9 Почленне дифер. Степ. Рядів. Рівномірна збіжність степеневих рядів.
- •10 Ряд Тейлора. Ряди Маклорена основних елементарних функцій.
- •11 Біоміальний ряд.
- •12 Ряд Фур’є з періодичної функції з періодичної функції.Теор Діріхле.
- •13 Ряд Фур’є для парних і непарних функцій.
- •14 Ряди Фур’є з довільним періодом. Ряд Фур’є функції заданої на дов. Проміжку. Теор. Діріхле.
- •15 Ряд Фур’є в комплексній Формі. Теорема Діріхле.
- •16 Інтеграл Фур’є в тригонометричній формі. Умови збіжності.
- •17 Інтеграл Фур’є в в комплексній формі.
- •18 Перетворення Фур’є в комплексній формі .Sin-,cos- перетворення Фур’є
- •19 Властивості перетворення Фур’є.
- •20 Похідна ф-ції комплексної змінної. Умови Коші – Рімана.
- •21 Геометричний зміст модуля.
- •22 Елементарні функції та їх властивості
- •23 Елементарні функції sinz;cosz;lnz
- •24 Обернено тригон.Функції та їх властивості.
- •25 Інтегра від функції комплексної змінної. Його властивості,формула обчислення(довести 4 власт)
- •26 Інтегральна теорема Коші. Узаг. Теорема коші.
- •27 Інтегр. Ф-ла Коші
- •28 Первісна функції комплексної змінної(довести самост.)
- •29 Ряд Тейлора(фкз). Формула Коші для похідної.
- •30 Ряд Лорана.
- •31 Особливі точки фкз. Їх класифікація.Ряд Лорана в усувн.Т.
- •32 Ряд Лорана в полюсі.
- •33 Лишки, їх обчислення. Обчислення лишків в полюсі. Лишки
- •Теорема Коші
- •34 Перетв Лапласа.Зображення деяких оригіналів
- •Доведення
- •35 Властивості перетворення Лапласа.
- •36 Теорема Бареля
- •37 Формула Рімана – Мелліна.
- •38 Знаходження оригіналів за допомогою лишків.
- •Доведення
- •39 Ітеграл Дюамеля
7 Почленне інтегрування та диференціювання раціональних рівнянь
Функціональний ряд, який є рівномірно збіжним на деякому інтервалі, можна почленно інтегрувати на цьому інтервалі.
Тобто,
якщо
 - рівномірно-збіжний на
,
інтервал
- рівномірно-збіжний на
,
інтервал
 то
то

Доведення:
Нехай
 відповідно
відповідно
 .
.
Розглянемо модуль різниці:
 ,
,
Нехай
члени ряду
- неперервно диференційовані
функції на інтервалі
,
ряд складений з похідних
 - є рівномірно збіжний на проміжку
.
Якщо при цьому вихідний ряд є збіжний
хоча б в одній точці
- є рівномірно збіжний на проміжку
.
Якщо при цьому вихідний ряд є збіжний
хоча б в одній точці
 то він є:
то він є:
а) рівномірно збіжний на інтервалі ;
б) його сума являє собою неперервно диференційовну функцію на інтервалі ;
в) ряд допускає почленне диференціювання, тобто похідна суми ряду дорівнює сумі похідних його членів.
Доведення:
Нехай
 .
Такий ряд, як рівномірно збіжний ряд з
неперервних функцій, допускає почленне
інтегрування на проміжку
.
Такий ряд, як рівномірно збіжний ряд з
неперервних функцій, допускає почленне
інтегрування на проміжку
 ,
при цьому ряд
,
при цьому ряд
 - є збіжним, отже, збігається і ряд
,
причому ця збіжність є рівномірною.
Оскільки
- є збіжним, отже, збігається і ряд
,
причому ця збіжність є рівномірною.
Оскільки
 ,
то диференціюючи цю рівність, переконуємось,
що ряд допускає по членне диференціювання.
,
то диференціюючи цю рівність, переконуємось,
що ряд допускає по членне диференціювання.
 .
.
8 Степеневі ряди. Теорема Абеля. Радіус збіжності.
Означення:
Функціональний ряд вигляду
 називається степеневим рядом в околі
точки
називається степеневим рядом в околі
точки
 .
.
Зауваження:
В певних випадках розглядатимуться
також степеневі ряди спеціального
вигляду у яких степені
 можуть бути від’ємними або не цілими.
можуть бути від’ємними або не цілими.
Теорема Абеля:
Якщо
степеневий ряд збігається при
![]() ,
то він абсолютно збігається і при всіх
значеннях
,
то він абсолютно збігається і при всіх
значеннях
 ,
таких що
,
таких що
![]() .
.
Доведення:

Якщо
ряд
 - збігається, то
- збігається, то
![]() ,
отже члени цього ряду є обмеженими
величинами. В той же час
,
отже члени цього ряду є обмеженими
величинами. В той же час
 ,
де
,
де
 .
.
Скориставшись мажорантно-мінорантною ознакою порівняння, можемо стверджувати, що ряд - є збіжним, оскільки він мажорується за абсолютною величиною сумою членів нескінченно спадної геометричної прогресії
9 Почленне дифер. Степ. Рядів. Рівномірна збіжність степеневих рядів.
Розглянемо
ряди, радіуси збіжності яких позначено,
відповідно через

;
 ;
;
 ;
;
О скільки
для третього з них
скільки
для третього з них


0
то, за граничною ознакою порівняння, радіус збіжності третього ряду не менше радіуса збіжності першого ряду.
Нехай
ряд
 збігається при
збігається при
 =
= ,
,
 тоді
тоді
 ,
де величина
,
де величина
 є обмежена.
є обмежена.
Нехай
 ,
тоді
,
тоді
 , але ряд
, але ряд
 збіжний за ознакою Даламбера, тобто
радіус збіжності третього ряду не більше
за радіус збіжності другого.
збіжний за ознакою Даламбера, тобто
радіус збіжності третього ряду не більше
за радіус збіжності другого.
10 Ряд Тейлора. Ряди Маклорена основних елементарних функцій.
Формула Тейлора для функції f(x):

Якщо
 ,
то за означенням:
,
то за означенням:

Для
функції sinx;
cosx;
ex;
ln(1+x);
shx;
chx
не
важко показати, що
 .
.
При х0=0:

11 Біоміальний ряд.
Якщо
розглянути формулу Тейлора для функції
 ,
то важко показати чому
,
то важко показати чому
 .
.
Розглянемо диференціальне рівняння:

Неважко
перевірити, що розв'язок:
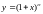 .
.
Як відомо задача Коші має єдиний розв'язок. Знайдемо розв'язок цього диф. рівняння у вигляді степеневого ряду:

Підставимо ці ряди в рівняння і одержимо тотожність:

Розкриємо дужки та прирівняємо коефіцієнти при однакових степенях:
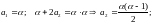

Оскільки задача Коші має єдиний розв'язок, то:

Дослідивши цей ряд за допомогою ознаки Даламбера одержимо:

Частинні випадки:

Підставимо
в останню формулу замість



Проінтегруємо цей ряд від 0 до х:

