Квантовая природа излучения

● Закон Стефана-Больцмана

,

где - энергетическая светимость (излучательность) черного тела; σ=5,67∙10^-8 Вт/м²К⁴ – постоянная Стефана-Больцмана; Т- термодинамическая температура.

● Связь энергетической светимости и спектральной плотности энергетической светимости или черного тела

.

● Энергетическая светимость «серого» тела

,

где А_Т – поглощательная способность «серого» тела.

● Закон смещения Вина

,

где - длина волны, соответствующая максимальному значению спектральной плотности энергетической светимости черного тела; b=2,9∙10^-3 м∙К - постоянная Вина.

● Зависимость максимальной спектральной плотности энергетической светимости черного тела от температуры

,

где С=1,29∙10^-5 Вт/(м³∙К⁵).

● Формула Релея-Джинса для спектральной плотности энергетической светимости черного тела

,

где k- постоянная Больцмана.

● Энергия кванта

,

где h=6,625∙10^-34 Дж∙с – постоянная Планка.

● Формула Планка

.

● Уравнение Эйнштейна для фотоэффекта

,

где hν – энергия фотона, падающего на поверхность металла; А_вых – работа выхода электрона из металла; - максимальная кинетическая энергия фотоэлектрона.

● «Красная граница» фотоэффекта для данного металла

,

где λ₀ – максимальная длина волны излучения ( ν₀ – соответственно минимальная частота), при которой фотоэффект еще возможен.

● Импульс фотона

.

● Давление, производимое светом при нормальном падении на поверхность,

,

где - облученность поверхности (энергия всех фотонов, падающих на единицу поверхности в единицу времени); ρ – коэффициент отражения;

- объемная плотность энергии излучения.

● Изменение длины волны рентгеновского излучения при комптоновском рассеянии

,

где λ и λ′ - длина волн падающего и рассеянного излучений; m₀ – масса электрона; θ – угол рассеяния; - комптоновская длина волны.

Примеры решения задач

Задача 1. Математический маятник длиной l₁=40 см и физический маятник в виде тонкого прямого стержня длиной l₂=60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние a центра масс стержня от оси колебаний.

Решение:

При синхронном колебательном движении маятников их периоды равны ,

где .

Отсюда

(1)

Момент инерции физического маятника определяется по теореме Штейнера:

(2)

Подставив (2) в (1), получим квадратное уравнение

(3)

Из (3) найдем два корня: a₁=10 см, a₂=30 см.

Таким образом, при одном и том же периоде колебаний физического маятника возможны два варианта расположения оси.

Величину (1) называют приведенной длиной физического маятника.

Ответ: a₁=10 см, a₂=30 см.

Задача 2. В вакууме распространяется плоская электромагнитная волна. Амплитуда напряженности магнитного поля волны 0,1 А/м. Определить энергию, переносимую этой волной через поверхность площадью 1 м², расположенную перпендикулярно направлению распространения волны, за время t = 1 с. Период волны T<< t.

Решение:

Плотность потока энергии электромагнитной волны определяется вектором Пойнтинга:

, где и – векторы напряженности электромагнитного и магнитного полей. Учитывая, что векторы и электромагнитной волны взаимно перпендикулярны, для модуля вектора p получим

p = EH.

Так как величины E и H в каждой точке волны меняются со временем по гармоническому закону, находясь в одинаковых фазах, то мгновенное значение p равно

p = E_m

Энергия, переносимая через площадку S, перпендикулярную направлению распространения волны, в единицу времени,

Учитывая, что в электромагнитной волне

найдем:

E_m = H_m

Тогда выражение (*) принимает вид

Энергия, переносимая волной за время t, равна

W =

По условию T<< t, поэтому ; тогда

W =

Подставляя числовые значения, получим

W = (0,1 А/м)² 1 м² 1 с = 1,88 Дж

Ответ: W = 1,88 Дж.

Задача 3. Радиусы кривизны поверхностей линзы R₁ = R₂ = 20 см. Определить: а) фокусное расстояние линзы в воздухе; б) фокусное расстояние этой же линзы, погруженной в жидкость (n_ж = 1,7). Показатель преломления материала линзы n_л = 1,5.

Решение:

Формула тонкой линзы

Применим данную формулу для случая (a), когда линза находится в воздухе, учитывая, что R₁ = R₂ = R

_отсюда

_{Для случая (б), когда линза погружена в жидкость}

_откуда

Ответ: F₁ = 0,2 м; F₂ = - 0,85 м

Задача 4. Установка для получения колец Ньютона освещается монохроматическим светом, падающим по нормали к поверхности пластинки. Наблюдение ведется в отраженном свете. Расстояние между вторым и двадцатым темными кольцами Δ τ_2,20 = 4,8 мм

Найти расстояние между девятым и шестнадцатым темными кольцами Ньютона.

Решение:

Радиус темных колец в отраженном свете определяется формулой:

τ_R = , где

𝑘 – порядковый номер кольца;

λ – длина волны;

R – радиус кривизны линзы.

Отсюда

1. Δ τ_2,20 = - = ( – )

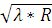2. Δ τ_9,16 = - = ( – ) =

Из (1) имеем

= , подставим в (2)

Δ τ_9,16 = = = 1,57 10 ^{– 3} м

Ответ: Δ τ_9,16 = 1,57 10 ^{– 3} м = 1,57 мм

Задача 5. На дифракционную решетку нормально падает монохроматический свет. Определить угол дифракции для линии λ₁ = 550 нм в четвертом порядке, если этот угол для линии λ₂ = 600 нм в третьем порядке составляет 30˚.

Решение:

Формула дифракционной решетки для двух линий

dsinφ₁ = 4 λ₁ (1)

dsinφ₂ = 3 λ₂ (2)

Поделим уравнение (1) на уравнение (2) и получим

= или =

откуда sinφ₁ = = = 0,61

φ₁ = arcsin 0,61 = 37˚42΄

Ответ: φ₁ = 37˚42΄

Задача 6. Найдите угол полной поляризации (i_Бр) при отражении света от стекла (n_c = 1,57), помещенного в воду (n_в = 1,33). Определить скорость света в воде.

Решение:

Согласно закону Брюстера tg i_Бр = при этом n₁ = n_в; n₂ = n_с

Тогда tg i_Бр = = 1,18, следовательно, i_Бр = arctg 1,18 ≈ 50˚

Абсолютный показатель преломления среды n = , тогда, зная n_в, найдем скорость распространения света в воде: V = = = 2,26 10⁸

Ответ: i_Бр ≈ 50˚; V = 2,26 10⁸

Задача 7. Температура внутренней поверхности электрической печи

T = 700˚C. Определите мощность излучения печи через небольшое отверстие диаметром d = 5 см, рассматривая его как излучение абсолютно черного тела.

Решение:

Из закона Стефана – Больцмана энергетическая светимость (излучательность) черного тела R = σ T ⁴. Другой стороны, N = R S, где S – площадь отверстия.

S = П τ ² = П ( ) ² = , подставим

N = R S = σ T ⁴ * = = 9,97 10¹ = 99,7 Вт

Ответ: N = 99,7 Вт

Задача 8. Красная граница фотоэффекта для металла λ_к = 6,2 10 ^{– 5} см. Найти величину запирающего напряжения для фотоэлектронов при освещении металла светом длиной волны λ = 330 нм.

Решение:

Запирающее напряжение – это напряжение на электродах, способное остановить электроны, вылетевшие из металла. Следовательно, работа сил электрического поля А_э равна кинетической энергии фотоэлектронов. А_э = Е_к или е U = Е_к. Кинетическую энергию определяем из уравнения Эйнштейна.

hν = A_вых + Е_к => E_к = hν - A_вых

Если известна красная граница фотоэффекта, то работа выхода определяется из выражения A_вых = h ν_к = h

Подставим е U = h - h = h C )

откуда U = -

U = = 1,76 В

Ответ: U = 1,76 В