3.2.3Числа с фиксированной запятой (точкой)

Нетрудно убедиться, что без каких-либо изменений в алгорит­мах выполнения арифметических операций рассмотренные методы кодирования целых чисел пригодны для обозначения дробей. Так, если договориться, что в четырехразрядных дополнительных кодах двоичная запятая, отделяющая целую часть от дробной, располо­жена посередине, то целочисленное действие 5 + ( — 1) = 4 можно интерпретировать как 1,25 + ( — 0,25) = 1,0.

Таким образом, для представления дробей программист может мысленно располагать двоичную запятую в любой нужной ему позиции. Естественно, при выполнении сложения и вычитания двоичные запятые должны быть расположены одинаково в обоих операндах, таково же будет и положение запятой в результате. Представление дробей, при котором положение двоичной запятой задается неявно в определенном месте машинного слова, называ­ется представлением с фиксированной запятой.

Неудобство такого представления проявляется при решении задач с величинами, которые могут сильно изменяться в сторону как очень малых, так и очень больших чисел. Например, в астрономических вычислениях может включаться масса электрона ( граммов) и масса Солнца ( граммов). Для представления таких чисел необходимо 34 разряда слева от десятичной запятой и 28 разрядов справа от нее. Это даст 62 значимых разряда в результатах. В действительности практически невозможно выполнить какие-либо измерения с точностью до 62 знаков (т.е. на практике значительная часть из этих разрядов оказалась бы равной нулю). Можно было бы хранить все промежуточные результаты с точностью до 62 значимых разрядов, а перед выводом окончательных результатов отбрасывать 50 или 60 разрядов, но процессор и память тратили бы на это слишком много времени.

Нужна такая система для представления чисел, в которой диапазон выражаемых чисел не зависит от числа значимых разрядов. Выход из затруднения состоит в отказе от фиксированного расположения запятой. Если разрешить запятой «плавать» во всех числах, то для выполнения операций над ними в записи каждого числа должна быть информация о месте располо­жения запятой. В тех случаях, когда эта информация выражена в записи чисел явным образом, говорят о представлении чисел с плавающей запятой.

3.2.4Числа с плавающей запятой (точкой)

3.2.4.1Представление чисел с плавающей запятой (точкой)

Наиболее удобным образом информация о положении запятой задается, если числа представлены в т. н. экспоненциальной форме записи. Это значит, что число записывается в виде произведения дроби со знаком (мантиссы) и основания системы счисления, возведенного в степень с некоторым показателем (порядком), например или .

Следует отметить ряд особенностей представления вещественных чисел в ЭВМ.

1. Область значений определятся по числу разрядов в экспоненте, а точность определяется по числу разрядов в мантиссе. Существует несколько способов представления того или иного числа, поэтому одна форма выбирается в качестве стандартной: мантиссу записывают в виде правильной дроби, у которой первая же цифра после запятой – значащая. Так 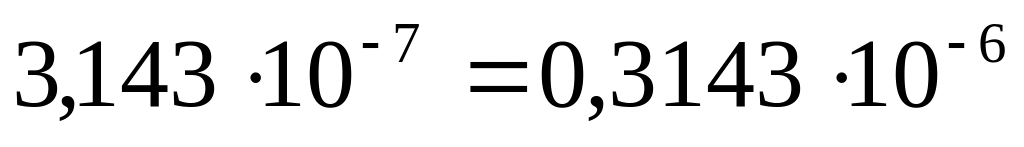, а . Такая форма экспоненциальной записи называется нормализованной. В резуль­тате изображение двоичного числа с плавающей запятой состоит из следующих компонентов: знаковый бит мантиссы, мантисса, порядок. Положение двоичной запятой в мантиссе неявно фиксируется слева от ее первой цифры.

2. Умножение - разрядных мантисс проще всего выполнить в виде - кратного цикла из операций сдвига и сложения с определением знака результата по хорошо известному пра­вилу знаков (для умножения и деления). Именно по этой причине мантиссу удобнее представлять не в дополнительном коде, а в представлении «знак-величина».

3. В отличие от умножения и деления при выполнении сложения и вычитания основную сложность составляют не собственно эти действия, а процедуры выравнивания. Как и в «ручных» операци­ях над числами в экспоненциальном представлении в первую очередь необходимо произвести сравнение порядков. Если они раз­личны, то мантисса операнда с меньшим порядком сдвигается вправо, а порядок, соответственно, увеличивается. Выравнивание производится до тех пор, пока порядки обоих операндов не сравняются. После этого производится сложение или вычитание мантисс. В процедурах сравнения порядков представление дополнительным кодом не очень удобно, поэтому-то порядок чисел с плавающей запятой обычно записывается в коде со смещением, упрощающем алгоритмы выравнивания.

Для пояснения принципа, положенного в основу двоичной нотации с плавающей точкой, рассмотрим пример, в котором для хранения числа используется всего один байт.

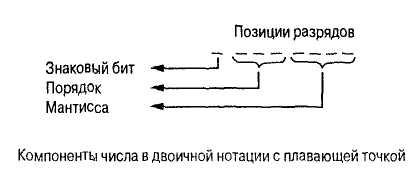
Условимся считать старший бит знаковым. Далее разделим оставшиеся биты байта на две группы, или поля, а именно: поле порядка числа к поле мантиссы. Следующие три бита после знакового бита будем считать полем порядка числа, а оставшиеся четыре бита — полем ман­тиссы. Описанный выше способ разделения байта представлен на рис.

Пример 1.

Пусть байт содержит битовую комбинацию 01101011. При разложении этой комби­нации по элементам описанного выше формата оказывается, что знаковый бит ра­вен 0, поле порядка числа имеет значение 110, а поле мантиссы – значение 1011. Для расшифровки представленного в этом байте значения, прежде всего, выделим мантиссу и поместим плавающую точку слева от нее: .1011

Далее выделим значение в поле порядка числа (110) и интерпретируем его как целое трехразрядное число, записанное в двоичной нотации с избытком 4. Таким образом, в поле порядка числа закодировано целое число 2. Это означает, что плавающую точку в полученном ранее значении следует пере­местить на два бита вправо (при отрицательном порядке плавающая точка пере­мещается влево), после чего будет получен окончательный результат: 10.11

Это значение является двоичным представлением числа 2³/₄. Наконец, определя­ем, что представляемое число является положительным, поскольку знаковый бит имеет значение 0. Таким образом, мы установили, что битовая комбинация 01101011 в двоичной нотации с плавающей точкой представляет число 2³/₄.

Пример 2.

Рассмотрим еще один пример, в котором байт содержит битовую комбинацию 10111100. Выделив мантиссу, получим следующее значение: .1100

Теперь перенесем плавающую точку на один бит влево, так как в поле поряд­ка содержится значение 011, представляющее число -1. Поэтому окончательный вид закодированного двоичного числа будет следующим: 0.01100

Это двоичное число имеет значение ³/₈. Закодированное в значении байта число является отрицательным, поскольку его знаковый бит равен 1. Из этого следует, что битовая комбинация 10111100 в двоичной нотации с плавающей точкой представляет число -³/₈.

Пример 3.

Для представления чисел в двоичной нотации с плавающей точкой необходи­мо следовать описанному выше процессу, но уже в обратном порядке. Например, для определения представления в этой нотации числа 2¹/₈ сначала необходимо записать его двоичное представление: 1.001. Затем эта битовая комбинация ко­пируется в поле мантиссы слева направо, начиная с самой левой единицы в дво­ичном представлении числа. Это будет выглядеть так:

Теперь остается заполнить поле порядка числа. Представим содержимое поля мантиссы, слева от которого расположена плавающая точка, и определим число разрядов, а также направление, в котором будет перемещаться плавающая точка для получения исходного значения двоичного числа. Понятно, что точка в комбинации .1001 должна быть переме­щена на один бит вправо; в результате будет получено исходное значение 1.001. Таким образом, порядок числа равен положительному числу 1, поэтому в соот­ветствующее поле следует поместить значение 101 (представляющее число +1 в двоичной нотации с избытком четыре). Окончательное значение в байте будет выглядеть следующим образом:

Важный момент: заполнение поля мантиссы всегда должно начинаться с крайней левой единицы в двоичном представлении кодируемого числа. Данное правило исключает возможность различного представления одного и того же значения.