Вычисл-е 2-го инт. В полярных коорд-х
0
– полюс и полярная полуось, r
– полярный радиус, φ – полярный угол;
r=|OM|,
r>0,
2π>φ
0
Полюс 0 полярной системы совмещается
с началом коорд-т, полярной осью считается
«+» часть Ох. R=arctg
x=rcos
φ, y=rsin
φ,
,
,
т.к. tg
– ф-я с периодом π, то формулу
используют
вместе с рисунком (определ. четверть)
Форм. перехода к полярн. коорд. в 2-м инт.
D – записан. в обл. D
в полярн. коорд-х; r—преобразование;
x=rcos φ,
y=rsin φ
Якобиан – определитель матрицы частных производных.
Внешний
всегда по φ. 1: r=r1(φ),
2: r=r2(φ)
Стрелка рисуется из начала корд-т.
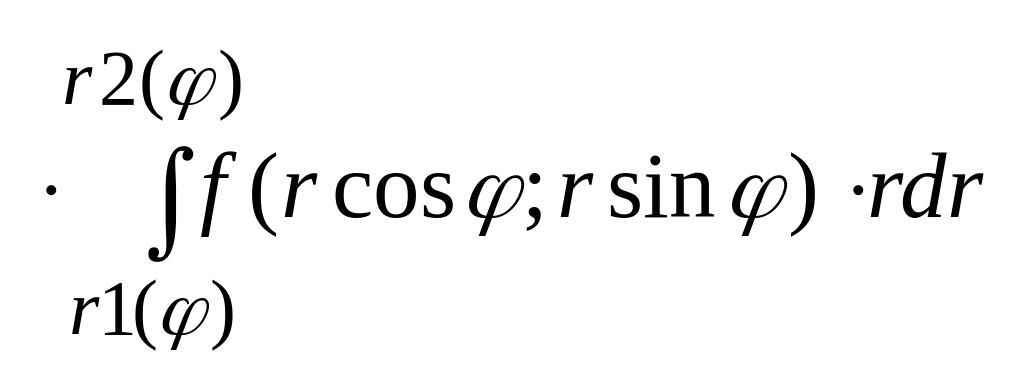Простейший
частный случай, если область это круг
с центром в нуле или круговой сектор.
замена переменных в 3ом интеграле. Якобиан. Вычисление интеграла в сферических и цилиндрических координатах.
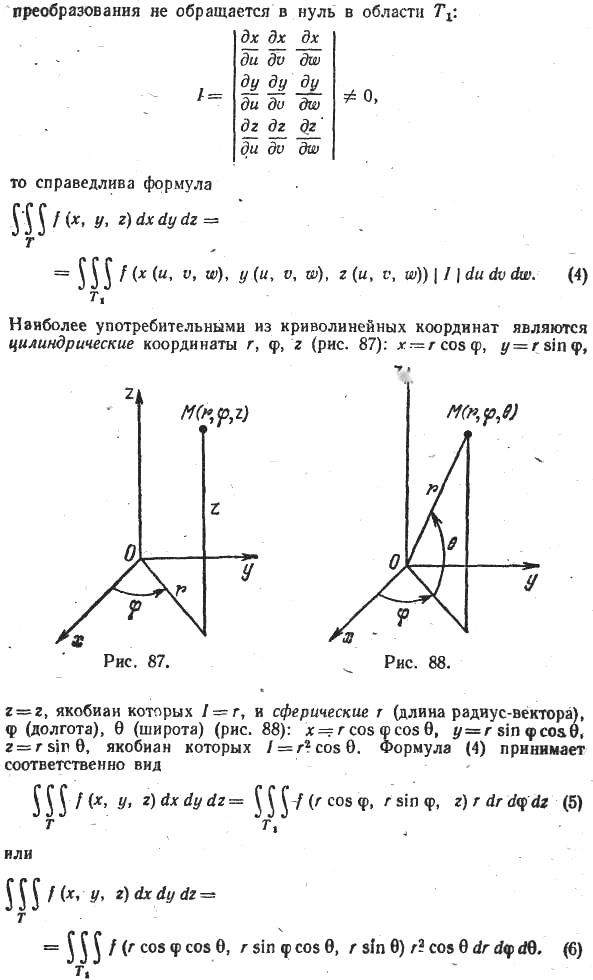Якобиан – определитель матрицы
частных производных. Цилиндрич.
Координаты
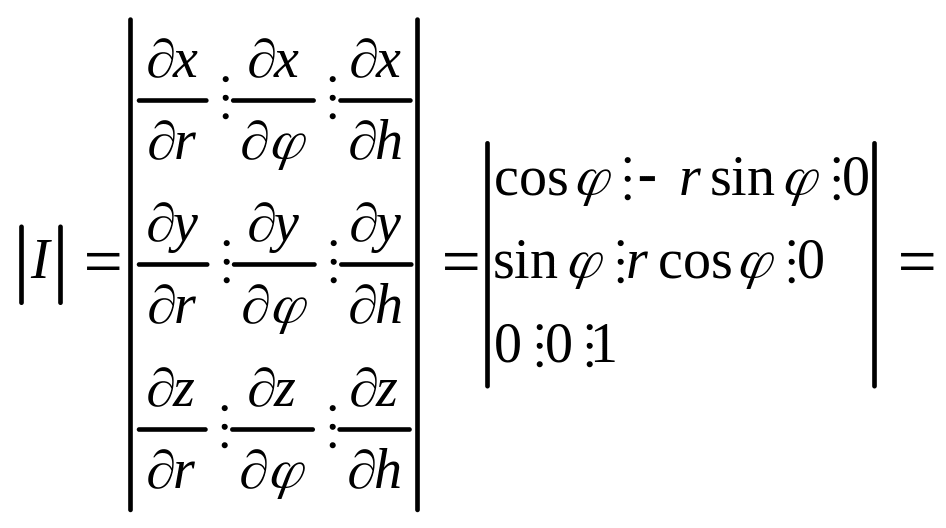
Формула
перехода от декартовых коорд-т к
цилиндрическим в
,
r-якобиан
преобр-я
– область V,
записан. в цилиндрич. координатах. V
цилиндра
Сфирические
координаты
;
|I|=r2sinθ
Формула перехода к
сфирическим коорд. в 3-м интеграле.
криволинейные интегралы 1 и 2 рода. Свойства и вычисление. Длина дуги кривой.
площадь произвольной поверхности. Интегралы по площади. Свойства и вычисление.
Поверхностные интегралы I-го рода (инт. по площади поверхности)
Пусть в 3-х мерном простр-ве задана некотор. поверх-ть G. Пусть в каждой точки поверх-ти задано скалярное поле F(x,y,z). Разби- ваем поверх-ть на части G1,G2,..Gn не- котор. гладкими кривыми. На каждой части берется произв. точка и вычисл. в этих точках знач-е скалярого поля F(Mk)=F(xk,yk,zk) образ. интегр. Сумма поверхностный интеграл 2 рода. Поток векторного поля. Примеры. Знач-е ф-и умнож. на полощадь соотв. части и произв. суммирование по k.
.
Рассм. предел интегр. суммы при стремелении
к 0 диаметра разбиения. Если этот предел
сущ., коне- чен и не зависит ни от способа
разби- ения, ни от выбора точек, то его
наз. по- верхностн. инт. по площади
поверх-ти (I-го
рода)
Условие
сущ-я: непрер-сть ф-и F(x,y,z)
на замкнут., ограничен. поверх-ти(т.е.
граница
поверх-ти).
Все св-ва инт. сохраняются. Вычисл-е
поверхност. инт. I-го
рода РИС.41
Пусть поверх-ть G
задана ур-ем
Z=Z(x,y).
Пусть любая прямая, || оси Oz
поверх-ть
G
только в одной точке. Пусть Gxy-
проекция поверх-ти G
на пл-ть Oxy,
тогда поверхностн. инт. вычисл. по
ф-ле:1)
2)
,
Gyx-проекция
поверх-ти G
на пл-ть Oyz.
Предполаг., что прямые || оси Ox
поверх-ть
в одной точке.
;3)y=y(x,y);
Gxy-проекция
поверх-ти G
на пл-ть Oxy.
Геометрич.,
физич. смысл
1)
,
то поверх-ть интег-я I-го
рода, то инт. представл. собой площадь
поверх-ти:
;
2)Если
-это
плот- ность массы, распредел. по по-
верх-ти, то поверх-ть интегр-я представ.
собой массу:
;
3)Если
плотность
электрич. Заряда, распредел. по поверх-ти
G,
то
представл
собой суммарн. эл. заряд поверх-ти.
поверхностный интеграл 2 рода. Поток векторного поля. Примеры.
Вычисление поверх. инт. II рода
.
Знак выбир. в
зависим от
:
если
,
то «+»
если
,
то «-». 1)Двойной инт. (справа) рассм. по
Gyz-
проекция поверх-ти G
на пл-ть Oyz;
2)Под- ставляем в функцию x=x(y,z);
3)Выбир. знак по
.
знак выбир. в зависим-ти от
.
знак
в зависим-ти от
.
скалярные и векторные поля, их основные характеристики: линии и поверхности уровня, градиент, дивергенция, ротор, циркуляция и др. виды полей.
теорема Остроградского – Гаусса, следствия из нее.
формулы Стокса и Грина, следствия из них.