Метод замены переменной (способ подстановки)
Пример
1. Найти
неопределенный интеграл
.
В
данном примере множитель
,
стоящий под знаком интеграла, есть
производная от выражения
,
стоящего в числителе, следовательно,
для нахождения интеграла воспользуемся
заменой:
,
.
Тогда:
.
Ответ:
.
ВОПРОС№35: Интегрирование рациональных функций.
Интегрирование дробно-рациональных функций.
Рассмотрим
правильную дробь
Представим
знаменатель в следующем виде:
.
Здесь
–
действительные корни многочлена, а
-
их
кратности. Дискриминанты квадратных
многочленовn
являются отрицательными числами, то
есть
Сумма
кратностей
Теорема о разложении правильной дроби на сумму простейших дробей
(без
доказательства). Верно
разложение
Здесь
–
некоторые вполне определенные числа.
С учетом этой теоремы задача интегрирования правильной рациональной дроби сводится к интегрированию выражений следующего вида:
I.
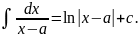
II.
Пусть
квадратный многочлен
px
q
имеет
отрицательный дискриминант, то есть
.
III.
Далее,
IV.
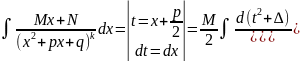
Первый интеграл, стоящий в правой части этого выражения, имеет вид интеграла из пункта II.
Обозначим
и
рассмотрим второй интеграл L(k)=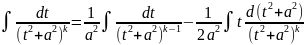
.
Второй
интеграл в этом выражении интегрируем
по частям
Следовательно,
будем иметь
Из этого рекуррентного соотношения можем вычислить любой интеграл L(k).
Пусть
теперь в (
)
n
m.
Тогда, разделив числитель на знаменатель,
представим (
)
в виде
+правильная дробь.
ВОПРОС№36:Определенный интеграл и его геометрический смысл. Свойства определенного интеграла.
Пусть функция f(x) определена на отрезке [a,b]. Разобьем этот отрезок
Точками a=x0<x1<...<xi<xi+1<...<xn=b.
Назовем
диаметром
этого
разбиения число d=
max(
–
),
i=1,
…. n-1.
Возьмем
[
]
и составим сумму
)(
которая называется интегральной
суммой.
Определение.
Число
I
называется
пределом интегральных сумм (
)(
)
при диаметре разбиения d
,
если
для
такое, что для всех разбиений с диаметром
d
<
и
для любого набора точек
выполняется неравенство
Теорема. Если предел интегральных сумм существует, то он единственен.
Доказательство.
Предположим,
что существуют два предела
.
Возьмем
любое число
.
Тогда для всех разбиений с достаточно
малым диаметром неравенство (
)
выполняется и для I1,
и для I2.
Следовательно,
Устремим
,
получим противоречие
.
Определение.
Предел
интегральных сумм (
)(
)
называется определенным
интегралом и
обозначается
.
Функция f(x) в этом случае называется интегрируемой на отрезке [a, b].
Г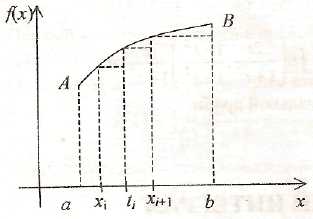
еометрический
смысл определенного интеграла
Рассмотрим задачу об определение площади криволинейной трапеции aABb (см. рис.).
Заменим криволинейную трапецию системой прямоугольников. Суммарная площадь этих прямоугольников определяется формулой ( )( ). Предел интегральных сумм ( )( ) при диаметре d и назовем площадью криволинейной трапеции. Итак, геометрический смысл определенного интеграла – это площадь криволинейной трапеции aABb.
Линейные свойства определенного интеграла
Пусть функция f(x) интегрируема на отрезке [a,b]. Тогда для ∀
c=const
интегрируемой
является функция cf(x)
и выполнено равенство
Доказательство. Пусть I= .
Тогда
для
>0
>0
такое,
что для всех разбиений с диаметром d
<
и
для любого набора точек
[
]
выполняется неравенство (
).
Следовательно,
при
2.
Пусть функции
(x),
(x)
интегрируемы на отрезке [a,b].
Тогда на этом отрезке интегрируемы их
сумма и разность и выполняется равенство
)
Доказательство.
Обозначим
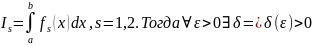такое,
что для всех разбиений с диаметром d
<
и
для любого набора точек
[
]
выполняются неравенства
Следовательно,
Это
означает, что
