
ВОПРОС№1: Множество и действия с ними. Свойства введенных операций.
Множество -
совокупность элементов, объектов,
отнесенных в единую группу по некоторым
признакам.
Примеры
множеств:
1.![]() -
множество натуральных чисел
-
множество натуральных чисел
2.![]() -
множество рациональных чисел.
-
множество рациональных чисел.
3.![]() -
множество целых чисел.
-
множество целых чисел.
4.![]() -
множество действительных чисел.
-
множество действительных чисел.
5.![]() -
множество комплексных чисел.
-
множество комплексных чисел.
Действия над множествами
1)Объединение множеств: Результатом объединения множеств A и B будет являться множество C такое, что любой элемент множества C является элементом либо множества A, либо множества B.
Операция объединения
множеств обозначается ![]()
2) Пересечение множеств: Результатом пересечения множеств A и B будет являться множество C такое, что любой элемент множества C является одновременно и элементом множества A, и элементом множества B.
Операция пересечения
множеств обозначается ![]()
3) Разность множеств: Результатом разности множеств A и B будет являться множество C такое, что любой элемент множества C является элементом множества A, и не является элементом множества B.
Операция разность
множеств обозначается: ![]()
4) Дополнение множества: Дополнением множества A до множества B будет являться множество C такое, что любой элемент множества C яв-ся элементом множества B,и не является элементом множества A.
Операция дополнения
множества обозначается
![]()
пример:
дано: А={1;3;6;8},
B={2;4;6;8}
Найти
объединение,пересечение и разность
множеств А и В.
Решение:
А ={1;2;3;4;6;8},
A∩B = {6;8}, A\B={1,3}
={1;2;3;4;6;8},
A∩B = {6;8}, A\B={1,3}
свойства введенных операций
A
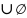 =A;
A∩
=A;
A∩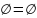 ;
A\
;
A\ =
;
=
;
 .
.Коммутативность операций объединения и пересечения
A B=B
A,
A∩B=B∩A
B=B
A,
A∩B=B∩A
Ассоциативность операций объединения и пересечения
(A
B)
С=A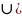 B
С);
A
B
С);
A B)
С=A
B)
С=A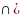 B
С)
B
С)
Идемпотентность операций объединения и пересечения
A A=A; A A=A
Дистрибутивность пересечения относительно объединения
A (B C)=(A B) (A C)
и дистрибутивность объединения относительно пересечения
A (B C)=(A B) (A C)
A\(A\B)=A B
A\(B C)=(A\B) (A\C), A\(B C)=(A\B) (A\C)
ВОПРОС№2: Отношение порядка на множестве действительных чисел и его свойства. Модуль действительного числа и его свойства.
Отношение порядка на множестве R. Для двух положительных действительных чисел
α= …
… ,
, …
… …
,
…
,
b=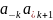 …
,
…
…
,
…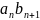 …
,
у которых до (n+1)-го разряда
одинаковые цифры, полагаем α<b тогда
и только тогда, когда
…
,
у которых до (n+1)-го разряда
одинаковые цифры, полагаем α<b тогда
и только тогда, когда
 <
< .
Если b-положительное число, а число
α-отрицательное или ноль, то всегда α<b.
Если α и b – отрицательные числа, то α<b
тогда и только тогда, когда
.
Если b-положительное число, а число
α-отрицательное или ноль, то всегда α<b.
Если α и b – отрицательные числа, то α<b
тогда и только тогда, когда
 <
< .
.
Свойства отношения порядка
Если α<b, b<c,то α<c
Если α<b,то существует действительное число с такое, что α<c<b
Модуль действительного числа и его свойства:
Модуль действительного числа α называется само число α, если оно нуль или положительное. Если α является отрицательным числом, то его модулем будет положительное число. Модуль обозначается
Свойства:
1) ![]() ,
причем
,
причем ![]() тогда
и только тогда, когда
тогда
и только тогда, когда ![]() .
2)
.
2) ![]() .
.
3) ![]() ;
в частности,
;
в частности, ![]() .
4)
.
4) ![]() ;
; ![]() .
5)
.
5) ![]() .
6)
.
6) ![]() ;
в частности
;
в частности ![]() и
и ![]() .
.
ВОПРОС№4: Уравнение прямой на плоскости. Геометрический смысл углового коэффицента.
Опред.1
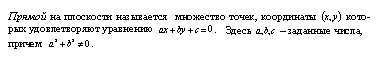
 -
уравнение прямой на плоскости.
-
уравнение прямой на плоскости.
у =
kх+β
– уравнение прямой через угловой
коэффициент.
=
kх+β
– уравнение прямой через угловой
коэффициент.
Геометрический смысл углового коэффициента
k= tgα – угловой коэффициент равен тангенсу угла между прямой и осью ОX.
ВОПРОС№5:Угол между двумя прямыми. Условие перпендикулярности и параллельности двух прямых. Расстояние от точки до прямой.
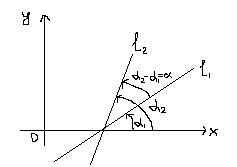
Угол
между прямыми L1
и L2
равен
tgα=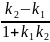

Условие параллельности 2-х прямых: k1=k2
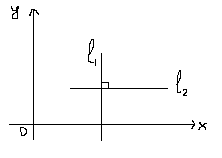
Условие перпендикулярности 2-х прямых: k1*k2= - 1
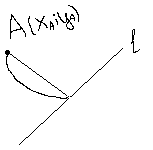
Расстояние от точки до прямой.
ρ(A;L)=
ВОПРОС№7: Каноническое уравнение эллипса
Теорема. В канонической для эллипса системе координат уравнение эллипса имеет вид:
![]() .
(4)
.
(4)
Доказательство. Доказательство проведем в два этапа. На первом этапе мы докажем, что координаты любой точки, лежащей на эллипсе удовлетворяют уравнению (4). На втором этапе мы докажем, что любоерешение уравнения (4) дает координаты точки, лежащей на эллипсе. Отсюда будет следовать, что уравнению (4) удовлетворяют те и только те точки координатной плоскости, которые лежат на эллипсе. Отсюда и изопределения уравнения кривой будет следовать, что уравнение (4) является уравнением эллипса.
1) Пусть точка М(х, у) является точкой эллипса, т.е. сумма ее фокальных радиусов равна 2а:
![]() .
.
Воспользуемся формулой расстояния между двумя точками накоординатной плоскости и найдем по этой формуле фокальные радиусы данной точки М:
![]() ,
, ![]() ,
откуда получаем:
,
откуда получаем:
![]() .
.
Перенесем один корень в правую часть равенства и возведем в квадрат:
![]() .
.
Сокращая, получаем:
![]() .
.
Приводим подобные, сокращаем на 4 и уединяем радикал:
![]() .
.
Возводим в квадрат
![]() .
.
Раскрываем
скобки и сокращаем на ![]() :
:
![]() ,
,
откуда получаем:
![]() .
.
Используя равенство (2), получаем:
![]() .
.
Разделив
последнее равенство на ![]() ,
получаем равенство (4),
ч.т.д.
,
получаем равенство (4),
ч.т.д.
2) Пусть теперь пара чисел (х, у) удовлетворяет уравнению (4) и пусть М(х, у) – соответствующая точка на координатной плоскости Оху.
Тогда из (4) следует:
![]() .
.
Подставляем это равенство в выражение для фокальных радиусов точки М:
![]()

![]() .
.
Здесь мы воспользовались равенством (2) и (3).
Таким
образом, ![]() .
Аналогично,
.
Аналогично, ![]() .
.
Теперь заметим, что из равенства (4) следует, что
![]() или
или ![]() и
т.к.
и
т.к. ![]() ,
то отсюда следует неравенство:
,
то отсюда следует неравенство:
![]() .
.
Отсюда, в свою очередь, следует, что
![]() или
или ![]() и
и
![]() ,
, ![]() .
(5)
.
(5)
Из равенств (5) следует, что , т.е. точка М(х, у) является точкой эллипса, ч.т.д.
Теорема доказана.
Определение. Уравнение (4) называется каноническим уравнением эллипса.
Определение. Канонические для эллипса оси координат называются главными осями эллипса.
Определение. Начало канонической для эллипса системы координат называется центром эллипса.
ВОПРОС№8:Каноническое уравнение гиперболы.
Гиперболой называется геометрическое место точек на плоскости, разность расстояний от каждой из которых до двух данных точек F1 и F2 (фокусов) есть величина постоянная.
Вывод уравнения гиперболы. Расстояние между фокусами обозначим через 2а.Тогда
a<c.
Систему координат выберем так, чтобы ось Ох проходила через фокусы гиперболы, а ось Оу делила расстояние между фокусами пополам.

Тогда //MF2/-/MF1//=2a => MF2-MF1=+-2a =>MF2=MF1+-2a./-модуль
Каноническое уравнение: x^2/a^2-y^2/b^2=1
a-действительная полуось
в-мнимая полуось
с=корень из a^2+b^2 -фокусное расстояние
прямые
x/a-y/b=0 и x/a+y/b=0 называются ассимптотами гиперболы.
Отношение с/а=E>1 называется эксцентриситетом гиперболы.
ВОПРОС№9:прямая линия и плоскость в пространстве.
Геометрическое место точек х;у на плоскости(R^2) удовлетворяющее уравнению ax+by+c=0 где а^2+b^2 не=0 называется прямой.
ах+ву+с=0 -общее уравнение прямой
у=kx+бета- уравнение прямой через угловой кофицент.

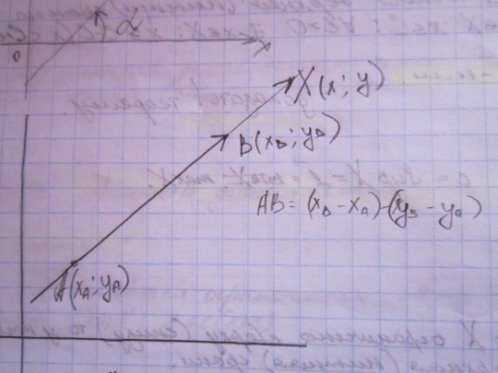
x-xA/xB-xA=y-yA/yB-yA
Угол между двумя прямыми в условиях параллельности и перпендикулярности двух прямых.

tgальфа=k^2-k1/1+k1k2
k1=k2 -прямые параллельны
Условия перпендикулярности:
k1*k2=-1
Расстояние от точки до прямой

р(A;L)=(/axA+byA+c/)модуль / корень a^2+b^2
ВОПРОС№10: Определения и основные действия с n-мерными векторами и их свойства.
Определение. Арифметическим n -мерным вектор-столбцом (или просто
n -мерным вектором) называется упорядочный набор из n действительных
чисел (1). Числа i x называются координатами вектора. Порядок чисел суще-
ственен.
Определение. Произведением n -мерного вектора x на число a€R называ-
ется вектор вида:

Определение.
Суммой
двух n
-мерных
векторов
 и
и
 называются
называются
n
-мерный
вектор
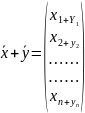
Нулевым вектором называется вектор, у которого все координаты равны
нулю.
Он обозначается
 .
.
Свойства введённых операций:
1.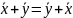 (коммуникативный закон сложения)
(коммуникативный закон сложения)
2.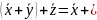 (ассоциативный закон сложения)
(ассоциативный закон сложения)
3.
4.
Для любого вектора
существует
вектор (-
)= такой,
что
такой,
что

5.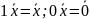
6. Для любых чисел a,b и для любого вектора выполнены равенства:
6.1. a( b ) = ( ab ) .
6.2. ( a + b ) = a + b
7.
Для любого числа a
и
для любых векторов
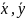 выполнено
равенство
выполнено
равенство
a(
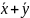 ) a
a
.
) a
a
.
Множество арифметических n -мерных векторов с введенными операциями
сложения и умножения векторов на действительные числа называется
n -мерным линейным вещественным пространством. Оно обозначается
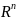 .
.
Пространство
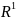 –
это числовая ось,
–
это числовая ось,
 –
числовая плоскость и так далее.
–
числовая плоскость и так далее.
Скалярное произведение векторов
Определение. Скалярным произведением двух n-мерных векторов называется число
<
 >=
>=

Свойства скалярного произведения
<
 >
= <
>
= <
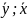 >.
>.<
 +…+
+…+ ≥0;
<
≥0;
<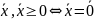
<
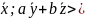 =
=

Норма вектора и ее свойство
Определение. Нормой вектора из называется число
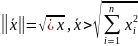
Свойства нормы
1. ≥0
и
≥0
и
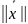 =0
⇔
=0
⇔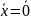
2.
Для любого числа a
и
для любого вектора
выполняется
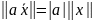 ,
в самом деле
,
в самом деле
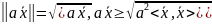
3.Для
любых векторов
выполнено неравенство

ВОПРОС№11:Скалярное произведение векторов и его свойства. Норма вектора



ВОПРОС№12: Определения, основные действия с матрицами и их свойства
