1.1. Основные понятия

Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины (или у столбцов одинаковой длины). Матрица записывается в виде

или, сокращенно,A=(a_ij) (i=1,m, j=1,n) i-номер строки,(т.е.i=1,2,3..m),j-номер столбца.

Матрицу А называют матрицей размера  m x n  и пишут Аmxn.Числа a_ij составляющие матрицу, называются ее элементами. Элементы, стоящие на диагонали, идущей из верхнего угла, образуют главную диагональ.

Матрицы равны между собой, если равны все соответствующие элементы этих матриц, т. е.

А=В,если a_ij=b_ij  (i=1,m, j=1,n)

Пример:

Квадратная матрица называется треугольной, если все элементы, расположенные по одну сторону от главной диагонали, равны нулю.

Матрица, все элементы которой равны нулю, называется нулевой. Обозначается буквой О.

В матричном исчислении матрицы О и E играют роль чисел 0 и 1 в арифметике.

Матрица, содержащая один столбец или одну строку, называется вектором (или вектор-столбец, или вектор-строка соответственно). Их вид:

Матрица размера 1х1, состоящая из одного числа, отождествляется с этим числом,

Т.Е. (5)1х1 есть 5.

Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается А^Т

 

 

 

Транспонированная матрица обладает следующим свойством: (А^Т)^Т=А

1.2. Действия над матрицами

Сложение

Операция сложения матриц вводится только для матриц одинаковых размеров.

Суммой двух матриц Amxn=(a_ij)  Bmxn=(b_ij) называется матрица Cmxn=(c_ij) такая, что c_ij=a_ij+b_ij  (i=1,m, j=1,n)

<< Пример 1.2

Аналогично определяется разность матриц.

Умножение на число

Произведением матрицы. A_mxn=(a_ij) на число k называется матрица B_mxn=(b_ij),такая, что.b_ij=k_*a_ij (i=1,m, j=1,n)

 << Пример 1.3

Матрица  -А = (-l)*A называется противоположной матрице А.

Разность матриц А-В можно определить так: А-В=А+(-В). Операции сложения матриц и умножения матрицы на число обладают следующими свойствами:

1. А+В=В+А

2. А+(В+С)=(А + В) + С

3. А+О=А

4. А-А=О

5. 1*А=А;

6. а*(А+В)=аА+аВ;

7. (а+в)*А=аА+вА

8. а*(вА)=(ав)*А,

где А, В, С — матрицы, а и в-числа.

Элементарные преобразования матриц

Элементарными преобразованиями матриц являются:

• перестановка местами двух параллельных рядов матрицы;

•  умножение всех элементов ряда матрицы на число, отличное от нуля;

• прибавление ко всем элементам ряда матрицы соответствующих элементов параллельного ряда, умноженных на одно и то же число.

 Две матрицы А и В называются эквивалентными, если одна из них       получается из другой с помощью элементарных преобразований. Записывается А ~ В.

При помощи элементарных преобразований любую матрицу можно привести к матрице, у которой в начале главной диагонали стоят подряд несколько единиц, а все остальные элементы равны нулю.

 Такую матрицу называют канонической, например

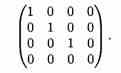
Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведение матрицы на матрицу называется матрица такая, что

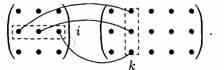
c_ik=a_i1*b_1k+a_i2*b_2k+…+a_in*b_nk. где (i=1,m, j=1,n)

т. е. элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-гo столбца матрицы В.

Получение элемента C_ik схематично изображается так:

 

Если матрицы А и В квадратные одного размера, то произведения АВ и ВА всегда существуют. Легко показать, что А*Е=Е*А=А, где А-квадратная матрица, Е-единичная матрица того же размера.

Матрицы А и В называются перестановочными, если АВ = ВА. Умножение матриц обладает следующими свойствами:

1. А*(В*С)=(А*В)*С;

2. А * (В + С) = АВ + АС

3. (А+В)*С=АС+ВС;

4. а(АВ) = (аА)В,

если, конечно, написанные суммы и произведения матриц имеют смысл. Для операции транспонирования верны свойства:

(A+B)^T=A^T+B^T

(АВ)^Т=В^TА^T  

. Свойства определителей.

Сформулируем основные свойства определителей, присущие определителям всех порядков. Некоторые из этих свойств поясним на определителях 3-го порядка.

Свойство 1. («Равноправность строк и столбцов»). Определитель не изменится, если его строки заменить столбцами, и наоборот.

Иными словами:

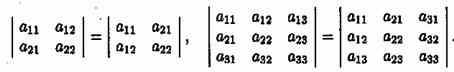
В дальнейшем строки и столбцы будем просто называть рядами определителя.

Свойство 2. При перестановке двух параллельных рядов определитель меняет знак.

Свойство 3. Определитель, имеющий два одинаковых ряда, равен нулю.

Свойство 4. Общий множитель элементов какого-либо ряда определителя можно вынести за знак определителя.

Из свойств 3 и 4 следует, что если все элементы некоторого ряда пропорциональны соответствующим элементам параллельного ряда, то такой определитель равен нулю.

 Действительно,

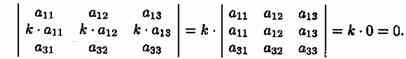
Свойство 5. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей.

Например,

Свойство 6. («Элементарные преобразования определителя»). Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число.

Дальнейшие свойства определителей связаны с понятиями минора и алгебраического дополнения.

Минором некоторого элемента a_ij определителя n-го порядка называется определитель (n-1)-го порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент. Обозначается m_ij

 

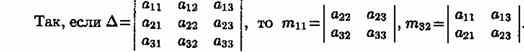
Алгебраическим дополнением элемента a_ij определителя называется его минор, взятый со знаком «плюс», если сумма i + j — четное число, и сознаком «минус», если эта сумма нечетная. Обозначается

 A_ij:  A_ij=(-1)^i+j_*m_ij.

Так A₁₁=+m₁₁,A₃₂=-m₃₂.

Свойство 7. («Разложение определителя по элементам некоторого ряда»). Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения.

Проиллюстрируем и одновременно докажем свойство 7 на примере определителя 3-его порядка. В этом случае свойство 7 означает, что

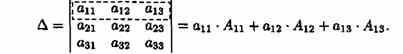
В самом деле, имеем

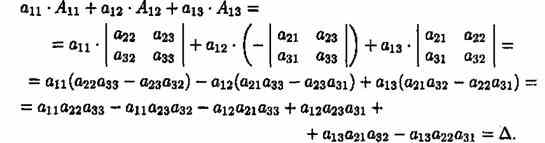
Свойство 7 содержит в себе способ вычисления определителей высоких порядков.

Свойство 8. Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю.

Так, например, a₁₁A₂₁+a₁₂A₂₂+a₁₃A₂₃=0.

ВОПРОС№13: Квадратные матрицы, их определители и способы их вычисления. Если число столбцов матрицы равно числу ее строк (I = J = N), то такая матрица называется квадратной. В этом разделе мы будем рассматривать только такие матрицы. Среди этих матриц можно выделить матрицы, обладающие особыми свойствами.

Единичной матрицей (обозначается I, а иногда E) называется матрица, у которой все элементы равны нулю, за исключением диагональных, которые равны 1, т.е.

важной характеристикой квадратной матрицы является ее определитель (обозначается det(A)). Определение определителя в общем случае довольно сложно, поэтому мы начнем с простейшего варианта — матрицы A размерностью (2×2). Тогда

Для матрицы (3×3) определитель будет равен

Определителем матрицы первого порядка, или определителем первого порядка, называется элемент, называется элемент  а₁₁:

.

ВОПРОС№14:Метод Гауса и Крамера решения СЛАУ.

Опред.1 Cистема вида , где a_ij – некоторые действительные числа называется система линейных алгебраических уравнений (СЛАУ).

Опред.2 Элементарные преобразовании системы это такие преобразования системы, когда исходная и преобразованная системы имеют одно и тоже решение.

1⁰ Умножение строки на любое число отличное от 0.

2⁰ Перестановка местами 2-х строк.

3⁰ Прибавление (вычитание) к строке любой другой строки, умноженной на некоторое число.

4⁰ вычеркивание нулевой строки.

Метод Гауса решения СЛАУ.

1⁰приведение исходной системы к системе ступенчатого вида с помощью элементарных преобразований.

2⁰ Решение системы ступенчатого вида.

3⁰ Запись общего решения.

Метод Крамера решения СЛАУ

1⁰ Находим определитель матрицы ∆=|A|

2⁰∆=0 (система не имеет решений)

3⁰ Находим ∆х; х=

4⁰ Находим ∆у; у=

5⁰ Находим ∆z; z

6⁰ Записываем ответ.

ВОПРОС№25: ПРОИЗВОДНАЯ ОБРАТНОЙ ФУНКЦИИ

Докажем теорему, позволяющую находить производную функции y=f(x), зная производную обратной функции.

Теорема. Если для функции y=f(x) существует обратная функция x=g(y), которая в некоторой точке у₀ имеет производную g '(v₀), отличную от нуля, то в соответствующей точке x₀=g(x₀) функция y=f(x) имеет производную f'(x₀), равную  , т.е. справедлива формула .

ВОПРОС№15:Определение и предел числовой последовательности. основные теоремы о числовых последовательностях.

Опред. Если каждому значению n=1,2,3… поставлено в соответствие действительное число a_n, то говорят, что задана числовая последовательность. Число а_n называется общим членом числовой последовательности, а сама последовательность обозначается {a_n} или просто а_n.

Предел числовой последовательности.

Опред. 1 Число А называется пределом числовой последовательности {a_n}, усли для любого ε>0 существует номер N=N(ε)такой, что |a_n-A|<ε для всех n>N.

Опред. 2 Число А называется пределом числовой последовательности (lim a_n=A,при n→∞), если начиная с некоторого номера все члены последовательности принадлежат интервалу a_n є (A-ξ; A+ξ).

Теорема 1( о единственности предела) Если последовательность имеет придел, то этот предел единственен.

Теорема 2 (оценочный признак существования предела) Пусть заданы три числовые последовательности a_n,b_n,c_n такие, что выполнены следующие условия: 1. a_n≤b_n≤c_n при всех n, начиная с какого-то номера. 2. a_n­→A, c_n→A. Тогда b_n→A.

Опред.1 Последовательность называется сходящейся, если существует ее предел.

Теорема1. (о пределе суммы, разности, произведения и частного двух числ. последовательностей)

Пусть a_n→A, b_n→B, тогда 1) (a_n+- b_n)→A+-B; 2) (a_n*b_n)→ A*B; 3) (a_n/b_n)→ A/B, если b_b≠0;B≠0.

Опред.2 Последовательность a_n – называется ограниченной сверху(снизу), если существует число С такое, что для любого номера n выполнено неравенство a_n≤C (a_n≥C).

Теорема о существовании предела монотонно возрастающей ограниченной последовательности. Число e.

Опред.1 последовательность a_n – называется монотонно возрастающей( убывающей), если для любого nєN выполнено неравенство a_n≤a_n+1

Теорема 1.Если последовательность a_n монотонно возрастает( убывает) и ограниченна сверху( снизу), то она имеет предел.

Число e - экспонента≈2,7.

ВОПРОС№16: Определение предела функции и основные теоремы.

Понятие предела функции является обобщением понятия предела последовательности, так как предел последовательности можно рассматривать как предел функции x _n = f(n) целочисленного аргумента n.

Пусть дана функция f(x) и пусть a - предельная точка области определения этой функции D(f), т.е. такая точка, любая окрестность которой содержит точки множества D(f), отличные от a. Точка a может принадлежать множеству D(f), а может и не принадлежать ему.

Определение 1. Постоянное число А называется пределом функции f(x) при x a, если для всякой последовательности {x _n } значений аргумента, стремящейся к а, соответствующие им последовательности {f(x _n )} имеют один и тот же предел А.

Это определение называют определением предела функции по Гейне, или “ на языке последовательностей ”.

Определение 2 . Постоянное число А называется пределом функции f(x) при x a, если, задав произвольное как угодно малое положительное число , можно найти такое >0 (зависящее от ), что для всех x, лежащих в -окрестности числа а, т.е. для x, удовлетворяющих неравенству  0 <  x-a <  , значения функции f(x) будут лежать в -окрестности числа А, т.е.  f(x)-A < .

Это определение называют определением предела функции по Коши, или “на языке - “.

Определения 1 и 2 равносильны. Если функция f(x) при x a имеет предел, равный А, это записывается в виде

                                                                                  .                                                                 (6.3)

В том случае, если последовательность {f(x _n )} неограниченно возрастает (или убывает) при любом способе приближения x к своему пределу а, то будем говорить, что функция f(x) имеет бесконечный предел, и записывать это в виде:

Переменная величина (т.е. последовательность или функция), имеющая своим пределом нуль, называется бесконечно малой величиной.

Переменная величина, имеющая бесконечный предел, называется бесконечно большой величиной.

Для нахождения пределов на практике пользуются следующими теоремами.

Теорема 1 . Если существуют пределы    

                                                 (6.4)

                                                           (6.5)

                                                     (6.6)

Замечание . Выражения вида 0/0, / , 0  , -  являются неопределенными, например, отношение двух бесконечно малых или бесконечно больших величин, и нахождение пределов такого вида носит название “раскрытие неопределенностей”.

Теорема 2.                                                                                        (6.7)

т.е. можно переходить к пределу в основании степени при постоянном показателе, в частности,   ;

                                                                                                                          (6.8)

                                                                                                                       (6.9)

Теорема 3.      

                                                                                                                                                                                      (6.10)

                                                                                                                                                                           (6.11)

где e 2.7 - основание натурального логарифма. Формулы (6.10) и (6.11) носят название первого и второго замечательного пределов.

ВОПРОС №18: Вертикальные и наклонные асимптоты

Асимптота - это прямая к которой график будет приближаться, но никогда её не пересечёт...она проходит параллельно оси у или х.

Вертикальные асимптоты

1. Линия задана уравнением y = f(x). Если 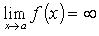 , то x = a –

вертикальная асимптота. В частности, если  , тоx = a –

вертикальная правосторонняя асимптота; если же  , то x = a - вертикальная левосторонняя асимптота.

2. Линия задана уравнениями x = x(t), y = y(t). Если 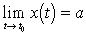 ,  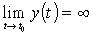, то x = a - вертикальная асимптота. В частности,

если  ,  , то x = a - вертикальная правосторонняя

асимптота; если же  ,  , то x = a - вертикальная левосторонняя асимптота.

Вертикальная асимптота — прямая вида при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:

1. 

2. 

Наклонные асимптоты  1. Линия задана уравнением y = f(x).

     Если  , то прямая y = kx + b - наклонная асимптота.

При этом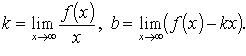 

     Если  , то прямая y = kx + b - наклонная асимптота

вправо,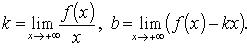 

     Если  , то прямая y = kx + b - наклонная асимптота

влево,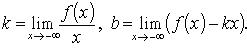 

     1. Линия задана уравнениями x = x(t), y = y(t).

     Если   (a - конечное число либо один из символов(  ) и линия обладает асимптотой y = kx + b,

то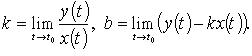 

Наклонная асимптота — прямая вида   при условии существования пределов

1. 

2. 

Замечание: функция может иметь не более двух наклонных(горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен  ), то наклонной асимптоты при  (или  ) не существует!

ВОПРОС№19: Определение и основные теоремы о непрерывных функциях.

Определение:   Функция f(x) , определённая в окрестности точки х0, называется непрерывной в этой точке, если существует её передел в этой точке и выполнено равенство:

Теорема (о знаке непрерывной функции). Пусть функция f(x) определена в некоторой окрестности точки х0 и непрерывна в этой точке. Пусть . Тогда в некоторой окрестности этой точки .

Теорема(о непрерывности суммы, разности, произведения и частного функций).Пусть функции определены в некоторой окрестности точки и непрерывны в этой точке. Тогда в этой точке непрерывна их сумма, разность, произведение. Если , то непрерывна в точке будет частное .

Теорема (о предельном значении непрерывной функции на сходящейся последовательности). Путь функция f(x)определена в некоторой окрестности точки и непрерывна в этой точке. Тогда для любой числовой последовательности выполнено равенство

Теорема( о непрерывности сложной функции). Пусть функция y=f(x) определена в окрестности точки и непрерывна в этой точке. Пусть функция z=F(y) определена в окрестности y0=f(x0) и непрерывна в этой точке. Тогда в некоторой окрестности точки определена сложная функция 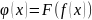, которая является непрерывной в точке .

Теорема( о нуле непрерывной на отрезке функции). Пусть функция f(x) непрерывна на отрезке и в концах этого отрезка она принимает значение разного знака. Тогда она обращается в нуль в некоторой точке этого отрезка.

Теорема (об ограничении непрерывной на отрезке функции) Если функция f(x) непрерывна на отрезке , то она ограничена на этом отрезке, то есть

Теорема (Вейерштрасса).Пусть функция f(x) непрерывна на отрезке . Тогда существует точка , в которой функция принимает наибольшее(наименьшее) значение, то есть

.

Теорема (о промежуточных значениях непрерывной функции). Пусть функция f(x)непрерывна на отрезке . Обозначим M(m) максимальное(минимальное) значение на этом отрезке. Тогда для любого числа найдётся точка такая , что f(t)=p.

ВОПРОС№20: Теорема существования и непрерывности обратной функции.

Теорема (о существовании и непрерывности обратной функции). Пусть на интервале (a,b) определена непрерывная возрастающая (убывающая)функция y=f(x). Обозначим

Тогда на интервале (А, В) определена обратная функция , которая возрастает(убывает) на этом интервале и является непрерывной в каждой точке этого интервала.

ВОПРОС№22: Дифференцируемые функции. Критерий дифференцируемости

Определение. Функция f, определенная в окрестности точки x , называется дифференцируемой в этой точке, если верна формула

f ( x штрих ▲x штрих ) -f ( x штрих ) Ai ▲xi ai( ▲x штрих )▲xi (3)

где i A – числа, а функции ai (▲ x штрих ) удовлетворяют условию

ai(▲ x штрих )→ 0 (i =1,2,…, n) при ▲x →0 . (4)

Теорема. Пусть функция f дифференцируема в точке x . Тогда в этой точке у нее существуют частные производные и выполнены равенства

(df( x штрих))/ (dxi)= Ai(i=1,2,…,n).

Доказательство. Из формулы (3) следует, что

(f ( x1 ,...,xi-1 ,xi+▲ xi ,xi+1,...,xn )- f ( x1 ,...,xi-1 ,xi ,xi+1 ,...,x n))/(▲Xi)= Ai+αi(▲Xi).

Переходя к пределу при ▲xi → 0 , получим равенство (5).

Теорема (достаточные условия дифференцируемости функции). Если функция f имеет частные производные по всем переменным в некоторой окрестности точки x штрих , причем все эти частные производные непрерывны в самой

точке x штрих , то указанная функция дифференцируема в этой точке.

Теорема (критерий дифференцируемости функции). Функция f x, определенная в окрестности точки x , дифференцируема в этой точке тогда и только тогда, когда существует производная f ׳x. При этом F f ׳x.

Доказательство. Пусть существует производная f ׳x . Обозначим

at=((f(t)-f(x)/t-x)-f׳ x

Тогда

ftfxt-xf׳xt-xαt,αt→0. (2)

Пусть теперь выполнено равенство (1) . Тогда

(f(t)-f(x)/t-xFαt,limαt0.

Следовательно, существует производная f ׳xF .

ВОПРОС№23: Производная суммы, разности, произведения и частного двух функций.

Производная суммы и разности

Пусть даны функции f(x) и g(x), производные которых нам известны. К примеру, можно взять элементарные функции, которые рассмотрены выше. Тогда можно найти производную суммы и разности этих функций:

1. (f + g)’ = f ’ + g ’

2. (f − g)’ = f ’ − g ’

Итак, производная суммы (разности) двух функций равна сумме (разности) производных. Слагаемых может быть больше. Например, (f + g + h)’ = f ’ + g ’ + h ’.

Строго говоря, в алгебре не существует понятия «вычитание». Есть понятие «отрицательный элемент». Поэтому разность f − g можно переписать как сумму f + (−1) · g, и тогда останется лишь одна формула — производная суммы.

• Задача. Найти производные функций: f(x) = x² + sin x; g(x) = x⁴ + 2x² − 3.

Решение. Функция f(x) — это сумма двух элементарных функций, поэтому:

f ’(x) = (x² + sin x)’ = (x²)’ + (sin x)’ = 2x + cos x;

Аналогично рассуждаем для функции g(x). Только там уже три слагаемых (с точки зрения алгебры):

g ’(x) = (x⁴ + 2x² − 3)’ = (x⁴ + 2x² + (−3))’ = (x⁴)’ + (2x²)’ + (−3)’ = 4x³ + 4x + 0 = 4x · (x² + 1).

Ответ: f ’(x) = 2x + cos x; g ’(x) = 4x · (x² + 1).

Производная произведения

Производная произведения считается совсем по другой формуле. А именно:

(f · g) ’ = f ’ · g + f · g ’

Формула несложная, но ее часто забывают. И не только школьники, но и студенты. Результат — неправильно решенные задачи.

• Задача. Найти производные функций: f(x) = x³ · cos x; g(x) = (x² + 7x − 7) · e^x.

Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’(x) = (x³ · cos x)’ = (x³)’ · cos x + x³ · (cos x)’ = 3x² · cos x + x³ · (− sin x) = x² · (3cos x − x · sin x)

У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’(x) = ((x² + 7x − 7) · e^x)’ = (x² + 7x − 7)’ · e^x + (x² + 7x − 7) · (e^x)’ = (2x + 7) · e^x + (x² + 7x − 7) · e^x = e^x · (2x + 7 + x² + 7x −7) = (x² + 9x) · e^x = x(x + 9) · e^x.

Ответ: f ’(x) = x² · (3cos x − x · sin x); g ’(x) = x(x + 9) · e^x.

Обратите внимание, что на последнем шаге производная раскладывается на множители. Формально этого делать не нужно, однако большинство производных вычисляются не сами по себе, а чтобы исследовать функцию. А значит, дальше производная будет приравниваться к нулю, будут выясняться ее знаки и так далее. Для такого дела лучше иметь выражение, разложенное на множители.

Производная частного

Если есть две функции f(x) и g(x), причем g(x) ≠ 0 на интересующем нас множестве, можно определить новую функцию h(x) = f(x)/g(x). Для такой функции тоже можно найти производную:

Неслабо, да? Откуда взялся минус? Почему g²? А вот так! Это одна из самых сложных формул — без бутылки не разберешься. Поэтому лучше изучать ее на конкретных примерах.

Задача. Найти производные функций: f(x) = x³ · cos x; g(x) = (x² + 7x − 7) · e^x.

Решение. Функция f(x) представляет собой произведение двух элементарных функций, поэтому все просто:

f ’(x) = (x³ · cos x)’ = (x³)’ · cos x + x³ · (cos x)’ = 3x² · cos x + x³ · (− sin x) = x² · (3cos x − x · sin x)

У функции g(x) первый множитель чуть посложней, но общая схема от этого не меняется. Очевидно, первый множитель функции g(x) представляет собой многочлен, и его производная — это производная суммы. Имеем:

g ’(x) = ((x² + 7x − 7) · e^x)’ = (x² + 7x − 7)’ · e^x + (x² + 7x − 7) · (e^x)’ = (2x + 7) · e^x + (x² + 7x − 7) · e^x = e^x · (2x + 7 + x² + 7x −7) = (x² + 9x) · e^x = x(x + 9) · e^x.

Ответ: f ’(x) = x² · (3cos x − x · sin x); g ’(x) = x(x + 9) · e^x

ВОПРОС№24: Дифференцирование сложной функции

теорема 1:

Пусть y= f(x) дифференцирована в точке x₀, а функция z=g(y) дифференцирована в точке x₀, тогда сложная функция z= g(f(x)) дифференцирована в точке x₀ и справедлива формула z= g’_y * f’(x); y=f(x)

y= f(x)	y= tg x
z= g(y)	z= y3
z= g(f(x))	z= tg3 x
z= g’y*f(x)	z= 3tg2x(tg x)’= 3tg2x+(1 : cos2x)

ВОПРОС№26: Локальные экстремумы и алгоритм его нахождения

Экстремум- максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума

Пусть дана функция   и   — внутренняя точка области определения f. Тогда

• x₀ называется точкой локального максимума функции f, если существует проколотая окрестность 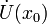  такая, что

• x₀ называется точкой локального минимума функции f, если существует проколотая окрестность   такая, что

Если неравенства выше строгие, то x₀ называется точкой строгого локального максимума или минимума соответственно.

• x₀ называется точкой абсолютного (глобального) максимума, если

• x₀ называется точкой абсолютного минимума, если

Значение функции f(x₀) называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.